Artikel ini adalah pembaruan dari artikel yang sama di blog lama saya di pikirsa.wordpress.com.
Saat belajar mengenai elektronika, elektrikal, listrik atau sistem daya, kadang-kadang jika kita memiliki rasa ingin tahu yang cukup baik maka kita akan bertanya-tanya,”Mengapa gelombang arus bolak-baik ‘selalu’ berbentuk gelombang sinus?”
Meskipun tentu nyatanya di seluruh penjuru bumi tidak selalu bentuk gelombang arus bolak-balik itu merupakan gelombang sinus. Tetapi memang bentuk paling dasar dari berbagai gelombang periodik memang gelombang sinus. Pertanyaannya adalah: mengapa? Ada juga yang bertanya mengapa bentuk gelombang sinus yang dipilih untuk sistem arus bolak-balik?
Pertama, sebenarnya tidak ada yang manusia yang memilih bentuk sinusoid untuk AC (alternating current), setidaknya sebatas pengetahuan saya (AFAIK). Bentuk gelombang itu adalah konsekuensi langsung dari sistem fisis yang ada. Khusus untuk sistem kelistrikan kita bisa dengan mudah menghubungkannya dengan bentuk umum generator pembangkit tegangan.
Lalu apa hubungannya antara bentuk generator dengan bentuk gelombang yang naik-turun-berbalik arah itu? Pertama-tama mari perhatikan bentuk dari generator yang disederhanakan.
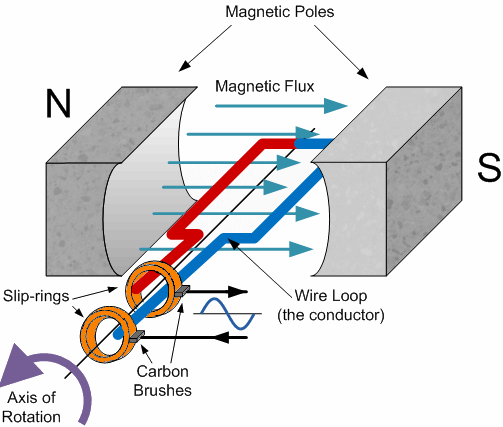 Gambar 1. Sumber gambar:
Gambar 1. Sumber gambar:
http://www.electronics-tutorials.ws/accircuits/sinusoidal-waveform.html
Untuk bisa memahami bagaimana tegangan dihasilkan dari perputaran rotor kita bisa melihat kembali aturan-tangan-kanan Fleming.
 Gambar 2. Sumber gambar: http://goo.gl/7zpXJE
Gambar 2. Sumber gambar: http://goo.gl/7zpXJE
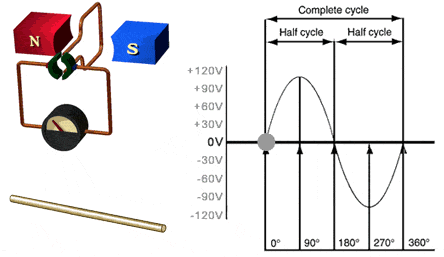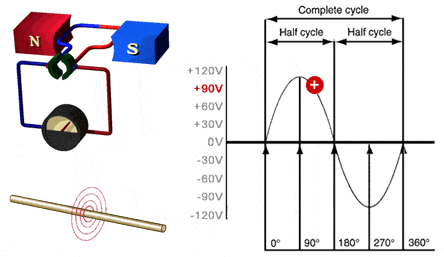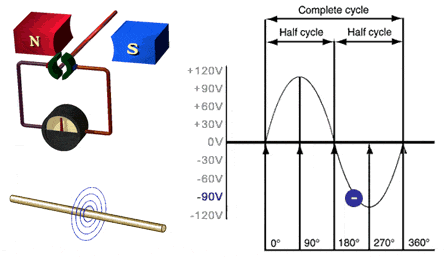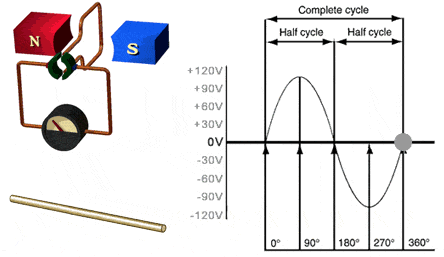 Gambar 3. Sumber gambar:
Gambar 3. Sumber gambar:
http://hvacreducation.net/ExampleLessons/module2_112-4.html
Dengan membandingkan antara Gambar 3 dengan Gambar 1, kita bisa melihat mengapa gelombang yang dihasilkan berupa gelombang sinus. Berikutnya untuk mendapatkan abstraksi yang lebih baik, kita bisa melihat pada Gambar 4 berikut.
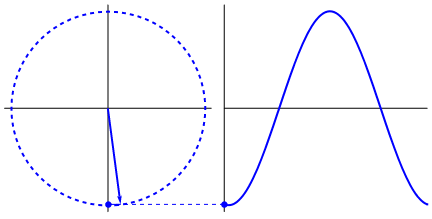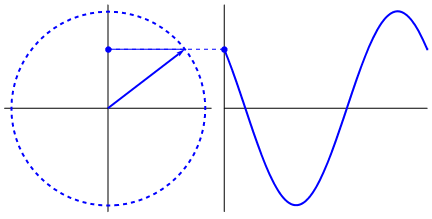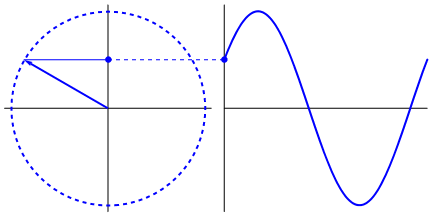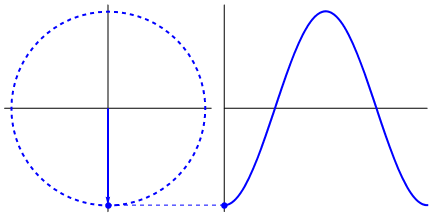 Gambar 4. Sumber gambar:
Gambar 4. Sumber gambar:
http://giphy.com/gifs/wave-ac-exchange-F5rQlfTXqCJ8c
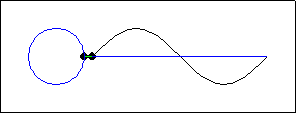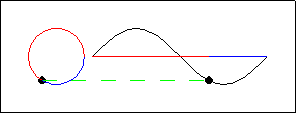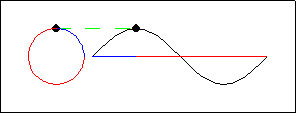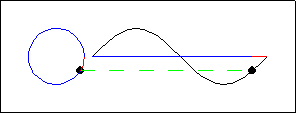 Gambar 5. Sumber gambar: http://goo.gl/i59TZl
Gambar 5. Sumber gambar: http://goo.gl/i59TZl
Gambar 5 memberikan tampilan animasi yang lebih lambat dari Gambar 4, sehingga kita bisa melihat dengan lebih seksama korelasi antara posisi rotor dengan pada titik-titik pada bentuk gelombang yang dihasilkan.
 Gambar 6. Sumber gambar:
Gambar 6. Sumber gambar:
http://www.technologyuk.net/mathematics/trigonometry/sine_function.shtml
Gambar 6 adalah sistem yang sama, hanya saja penempatan “generator” dan gelombang tegangan keluaran saja yang ditukar posisinya.
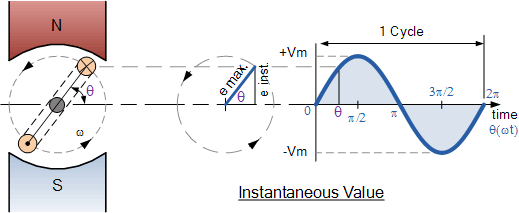 Gambar 7. Sumber gambar:
Gambar 7. Sumber gambar:
http://www.electronics-tutorials.ws/accircuits/sinusoidal-waveform.html
Untuk setiap saat tertentu (instantaneous) kita dapat menghitung berapa nilai tegangan saat itu sebagai fungsi dari sudut fase generator.
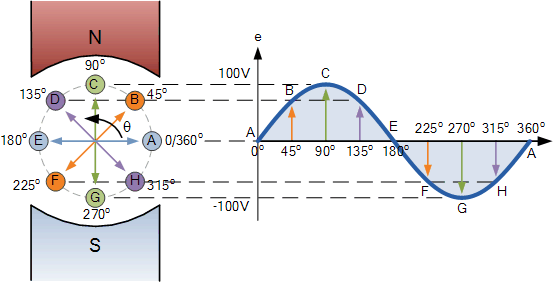 Gambar 8. Sumber gambar:
Gambar 8. Sumber gambar:
http://www.electronics-tutorials.ws/accircuits/sinusoidal-waveform.html
Pada Gambar 8 diperlihatkan beberapa posisi untuk sudut kelipatan 45°.
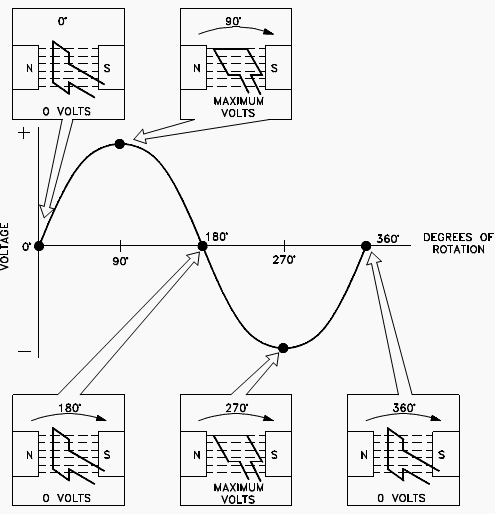 Gambar 9. Korelasi loop pada rotor dengan gelombang tegangan
Gambar 9. Korelasi loop pada rotor dengan gelombang tegangan
Sumber gambar: http://goo.gl/4dO9KJ
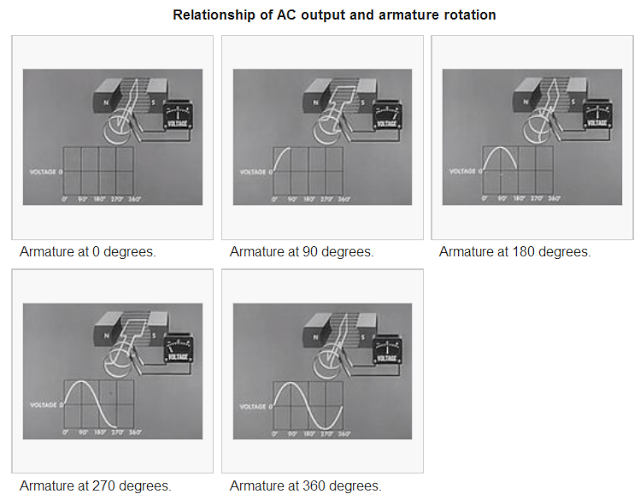 Gambar 10. Sumber gambar:
Gambar 10. Sumber gambar:
https://en.wikipedia.org/wiki/Single-phase_generator
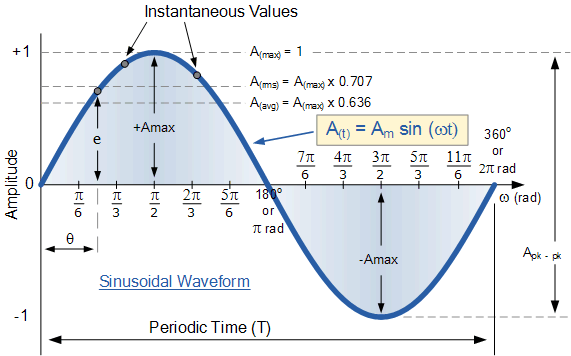 Gambar 11. Persamaan untuk menghitung nilai tegangan sesaat.
Gambar 11. Persamaan untuk menghitung nilai tegangan sesaat.
Sumber gambar: http://www.electronics-tutorials.ws/accircuits/sinusoidal-waveform.html
 Gambar 12. Sumber gambar:
Gambar 12. Sumber gambar:
http://tinkerine.com/pseudo-sine-wave-generator-ditto/
Pada Gambar 12, kita bisa melihat bagaimana bentuk sinusoid dapat dihasilkan dari “generator” sederhana seperti itu.
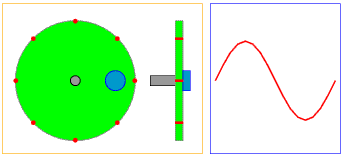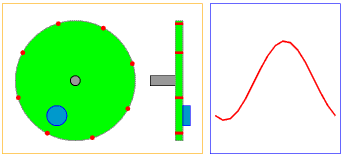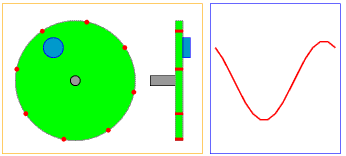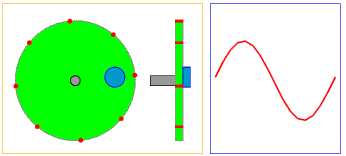 Gambar 13. Sumber gambar: https://goo.gl/tf8LYR
Gambar 13. Sumber gambar: https://goo.gl/tf8LYR
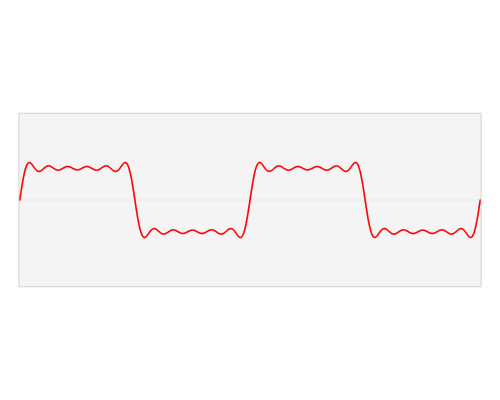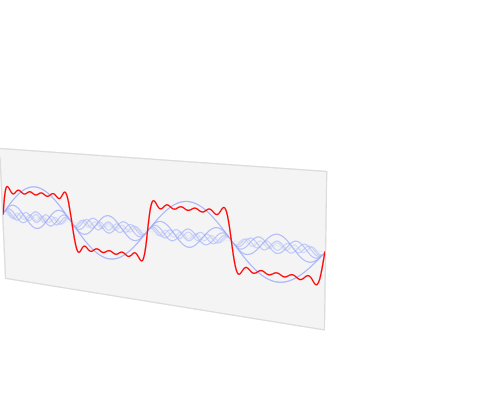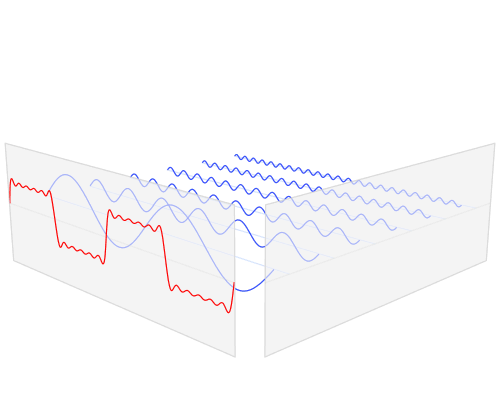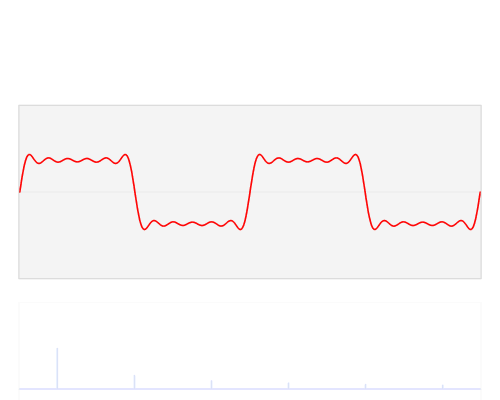
Jika pada gambar-gambar sebelumnya kita melihat hanya dari satu sudut pandang saja, maka pada Gambar 13 kita bisa melihat dari dua sudut pandang. Yang pertama, tepat dari arah depan, persis seperti pada gambar-gambar sebelumnya dan satu dari samping. Dengan cara ini kita bisa melihat dimensi yang berbeda dari satu fenomena yang sama.
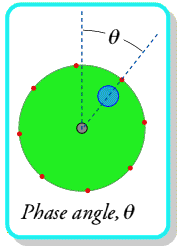 Gambar 14. Sumber gambar: https://goo.gl/tf8LYR
Gambar 14. Sumber gambar: https://goo.gl/tf8LYR
 Gambar 15. Sumber gambar: https://goo.gl/tf8LYR
Gambar 15. Sumber gambar: https://goo.gl/tf8LYR
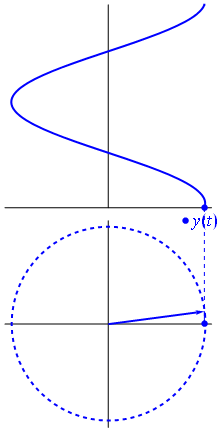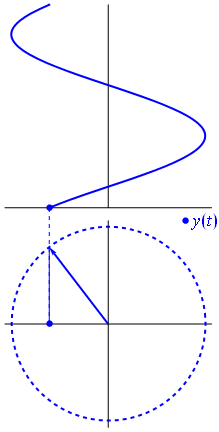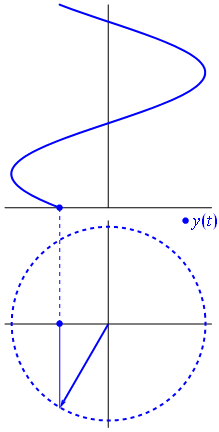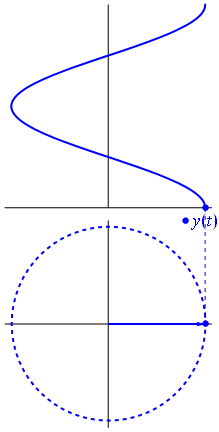 Gambar 16. Sumber gambar:
Gambar 16. Sumber gambar:
https://en.wikipedia.org/wiki/Phasor
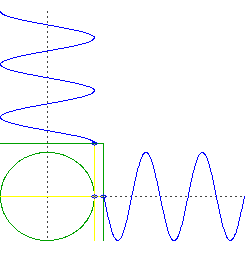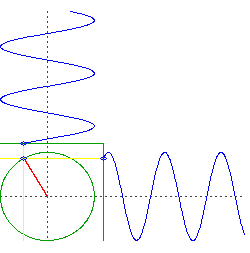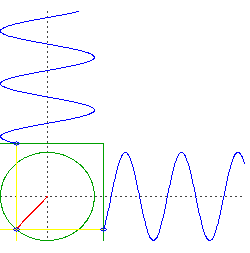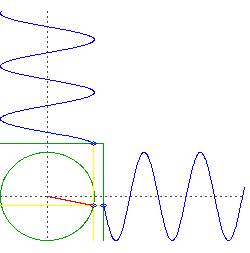 Gambar 17. Sumber gambar: http://goo.gl/Q12G6K
Gambar 17. Sumber gambar: http://goo.gl/Q12G6K
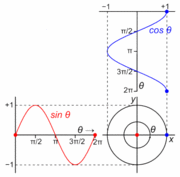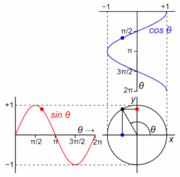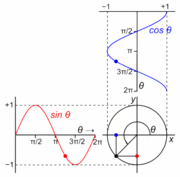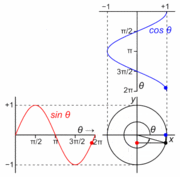 Gambar 18. Sumber gambar:
Gambar 18. Sumber gambar:
https://en.wikipedia.org/wiki/Talk%3ASimple_harmonic_motion
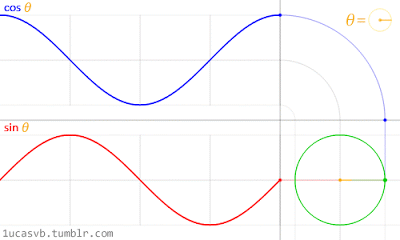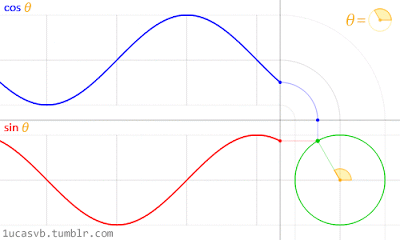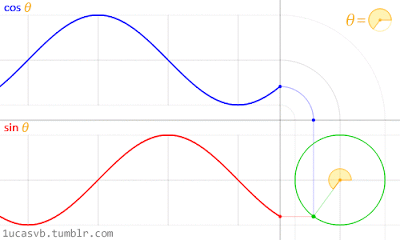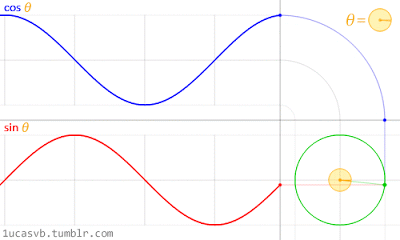 Gambar 19. Sumber gambar:
Gambar 19. Sumber gambar:
http://www.iflscience.com/brain/math-gifs-will-help-you-understand-these-concepts-better-your-teacher-ever-did
 Gambar 20. Sumber gambar: http://www.gailruby.com/SHMGraph.htm
Gambar 20. Sumber gambar: http://www.gailruby.com/SHMGraph.htm
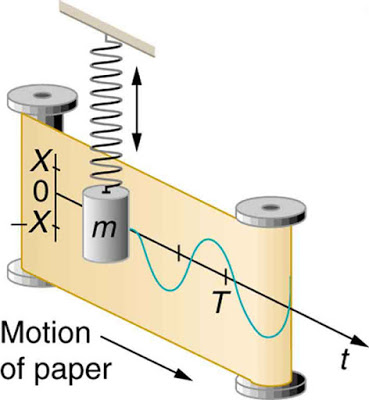 Gambar 21. Sumber gambar: http://goo.gl/x765kH
Gambar 21. Sumber gambar: http://goo.gl/x765kH
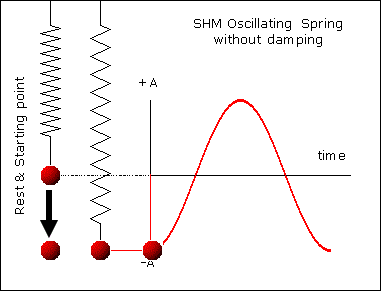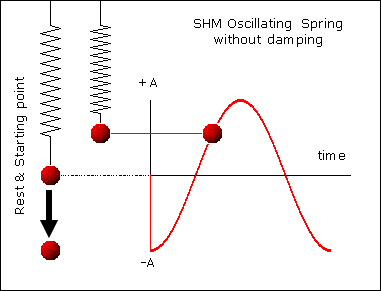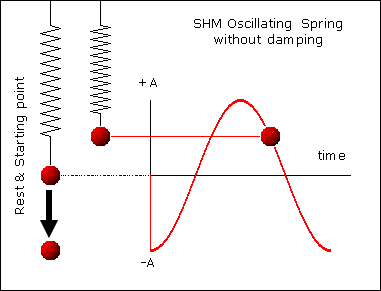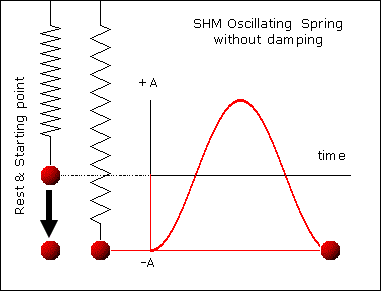 Gambar 22. Sumber gambar:
Gambar 22. Sumber gambar:
http://www.mysearch.org.uk/website1/html/221.SHM.html
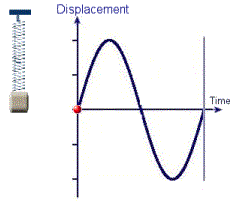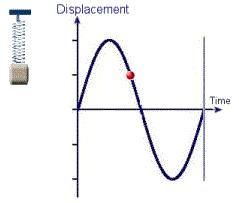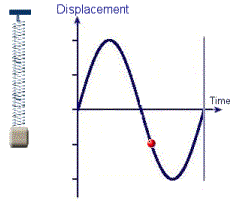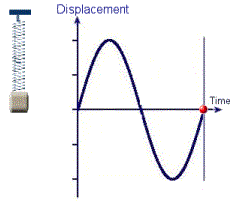 Gambar 23. Sumber gambar:
Gambar 23. Sumber gambar:
http://www.rmcybernetics.com/projects/experiments/experiments_resonance_simple_harmonic_motion.htm
UPDATE 24/09/2015
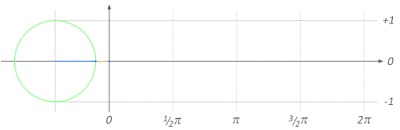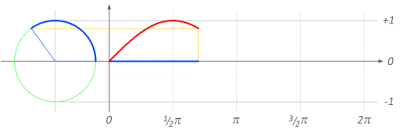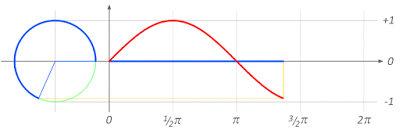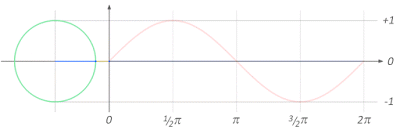 sumber: http://math-is-beautiful.tumblr.com/
sumber: http://math-is-beautiful.tumblr.com/
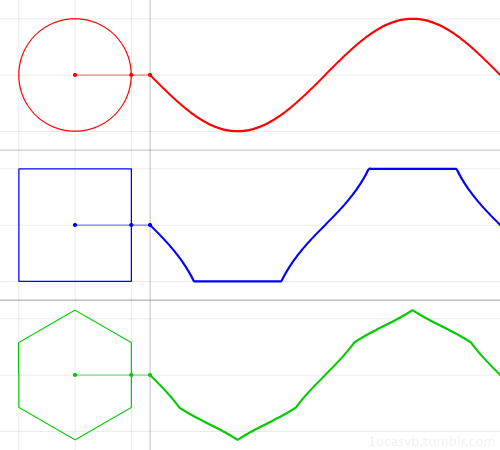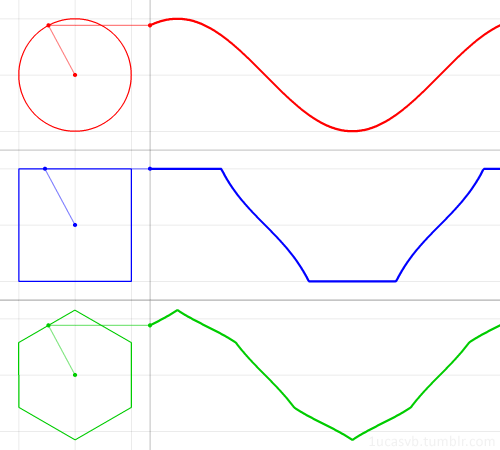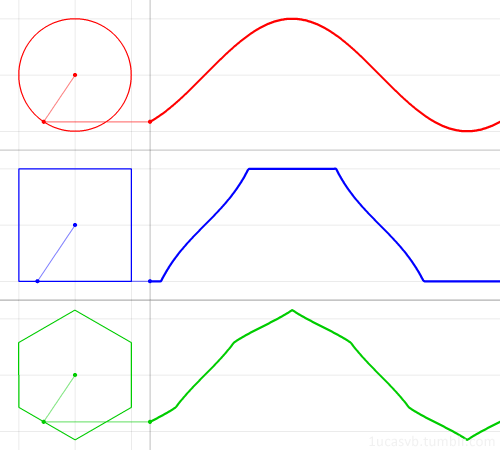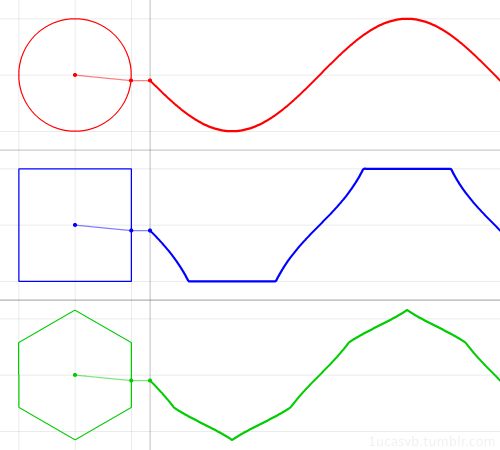 sumber: http://rebloggy.com/
sumber: http://rebloggy.com/
font cache: Ψ α β π θ μ Φ φ ω Ω ° ~ ± ≈ ≠ ≡ ≤ ≥ ∞ ∫ • ∆
Referensi tambahan:
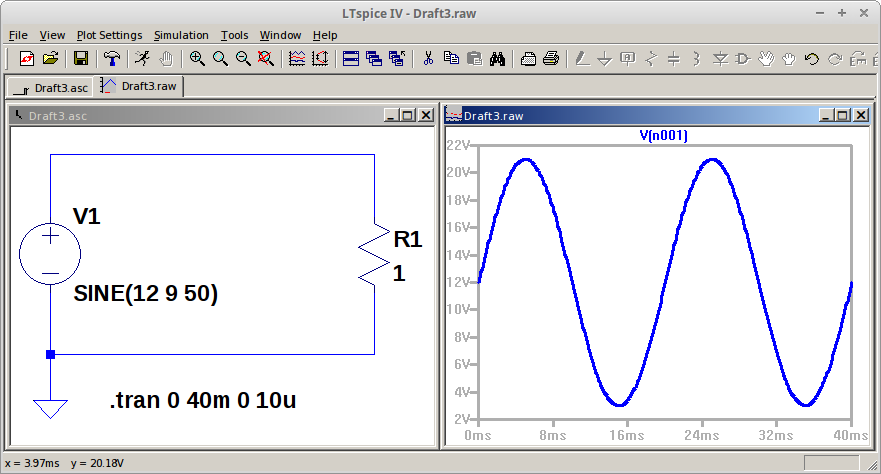 Gambar 1.
Gambar 1.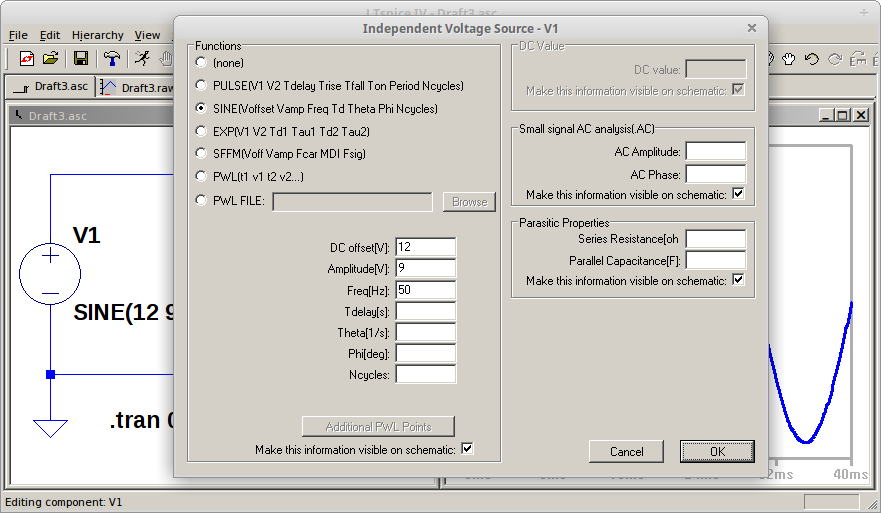 Gambar 2.
Gambar 2.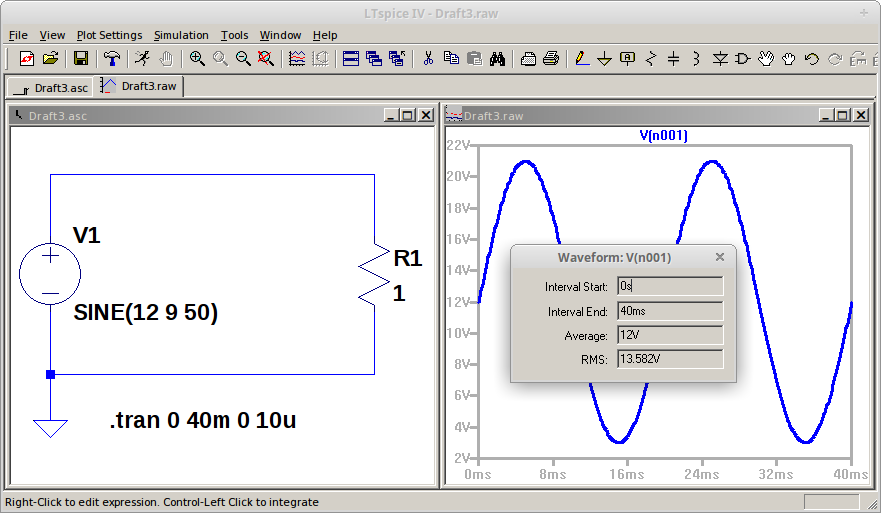 Gambar 3.
Gambar 3.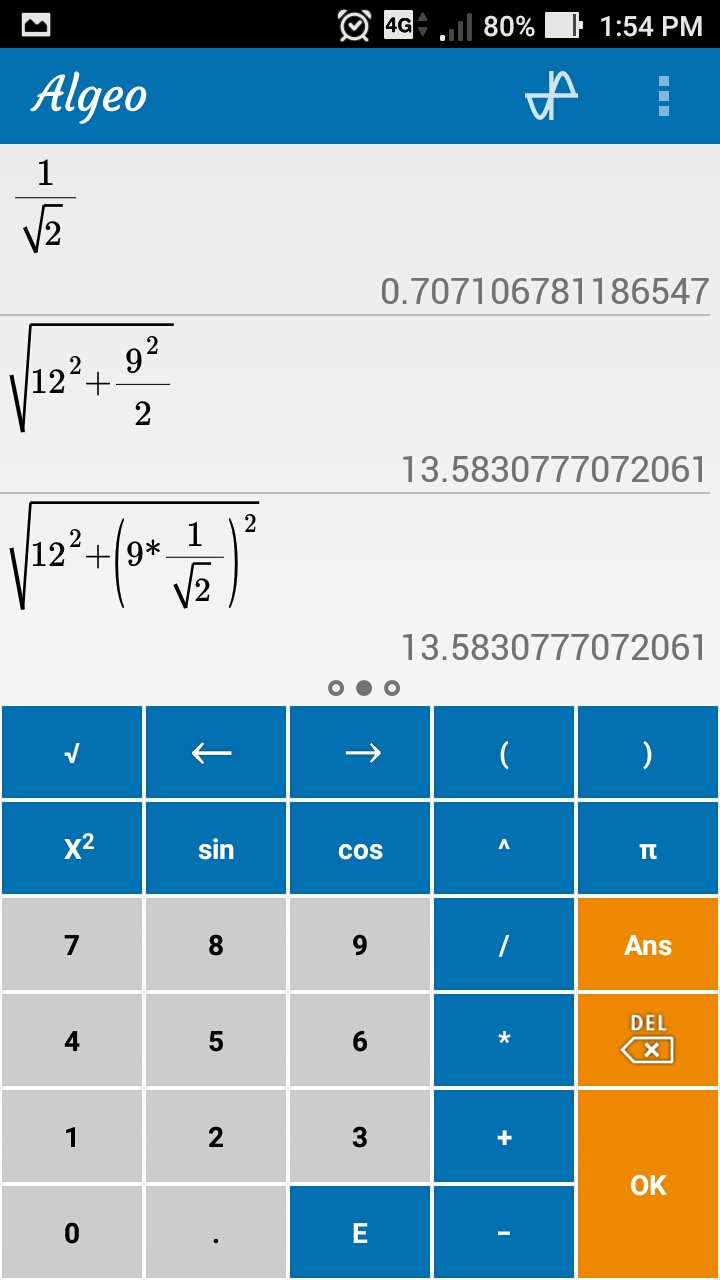 Gambar 4. Perhitungan nilai tegangan RMS (AC+DC) dengan Algeo.
Gambar 4. Perhitungan nilai tegangan RMS (AC+DC) dengan Algeo.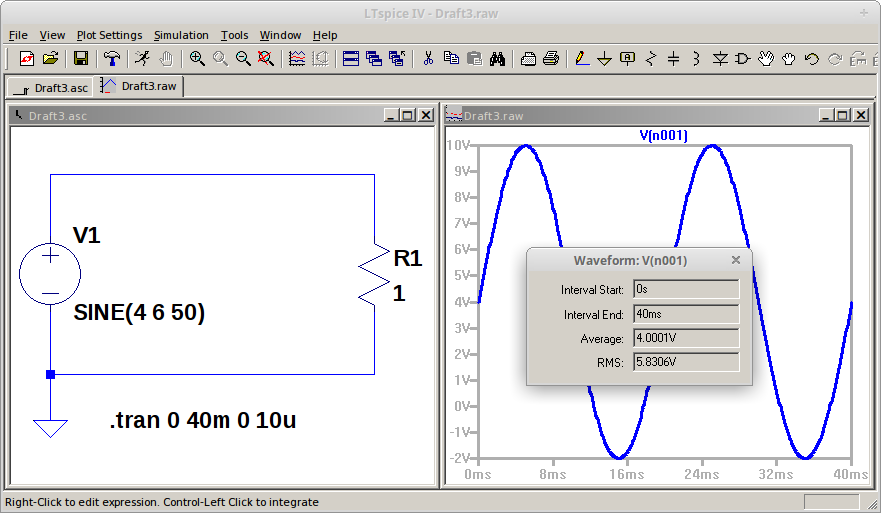 Gambar 5. Simulasi gelombang sinus dengan offset, puncak nilai positif dan negatif.
Gambar 5. Simulasi gelombang sinus dengan offset, puncak nilai positif dan negatif.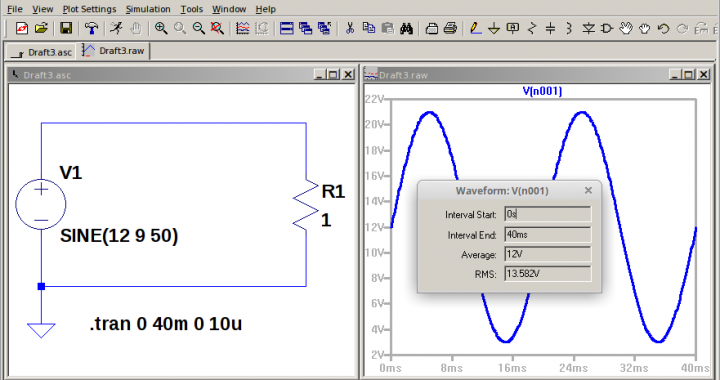

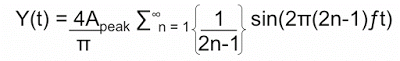

 Gambar 1. Sumber gambar:
Gambar 1. Sumber gambar: Gambar 2. Sumber gambar:
Gambar 2. Sumber gambar:  Gambar 3. Sumber gambar:
Gambar 3. Sumber gambar: Gambar 4. Sumber gambar:
Gambar 4. Sumber gambar: Gambar 5. Sumber gambar:
Gambar 5. Sumber gambar:  Gambar 6. Sumber gambar:
Gambar 6. Sumber gambar: Gambar 7. Sumber gambar:
Gambar 7. Sumber gambar: Gambar 8. Sumber gambar:
Gambar 8. Sumber gambar: Gambar 9. Korelasi loop pada rotor dengan gelombang tegangan
Gambar 9. Korelasi loop pada rotor dengan gelombang tegangan Gambar 10. Sumber gambar:
Gambar 10. Sumber gambar: Gambar 11. Persamaan untuk menghitung nilai tegangan sesaat.
Gambar 11. Persamaan untuk menghitung nilai tegangan sesaat. Gambar 12. Sumber gambar:
Gambar 12. Sumber gambar: Gambar 13. Sumber gambar:
Gambar 13. Sumber gambar:  Gambar 14. Sumber gambar:
Gambar 14. Sumber gambar:  Gambar 15. Sumber gambar:
Gambar 15. Sumber gambar:  Gambar 16. Sumber gambar:
Gambar 16. Sumber gambar: Gambar 17. Sumber gambar:
Gambar 17. Sumber gambar:  Gambar 18. Sumber gambar:
Gambar 18. Sumber gambar: Gambar 19. Sumber gambar:
Gambar 19. Sumber gambar: Gambar 20. Sumber gambar:
Gambar 20. Sumber gambar:  Gambar 21. Sumber gambar:
Gambar 21. Sumber gambar:  Gambar 23. Sumber gambar:
Gambar 23. Sumber gambar: sumber:
sumber:  sumber:
sumber: