Tahukah anda cerita mengenai silang pendapat tentang benda yang disebut sebagai seekor gajah?
http://www.nature.com/ki/journal/v62/n5/fig_tab/4493262f1.html
Kali ini kita akan melihat “seekor gajah” dari salah satu sisi. Kita kenali salah satu bagian yang (bersama bagian yang lain) membuat sebuah benda dinamai “gajah”.
Gelombang sinusoida dapat dipakai sebagai dasar untuk membentuk gelombang lain, misalnya gelombang kotak. Dengan kata lain suatu gelombang kotak dapat didekonstruksi menjadi beberapa gelombang sinusoida.
Berikut adalah beberapa contoh gambar dari beberapa sumber di Internet yang memperjelas konsepnya secara sederhana. Pertama mari melihat dua buah gelombang sinus yang memiliki amplitudo yang sama (puncak yang tingginya sama) tetapi berbeda nilai frekuensinya.
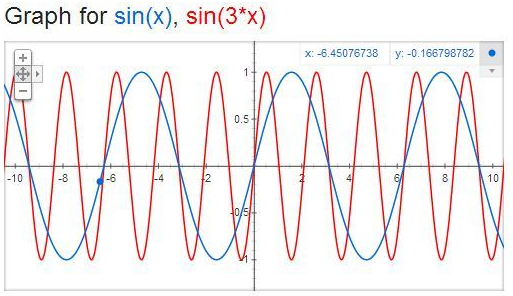Gambar 1. sumber gambar: [1]
Gambar 1 adalah visualisasi pada ranah waktu (time domain) sedangkan gelombang yang sama bisa digambarkan dengan cara yang berbeda di ranah frekuensi (frequency domain) seperti yang diperlihatkan pada Gambar 2.
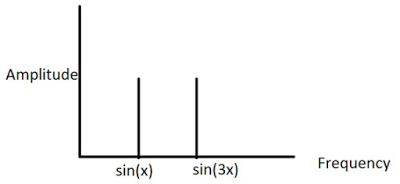Gambar 2. sumber gambar: [1]
Bisa dilihat pada Gambar 2 bahwa nilai frekuensi untuk dua gelombang adalah jelas berbeda (x dan 3 kali x), tetapi besar nilai amplitudonya sama. Diwakili oleh ruas garis yang tingginya sama.
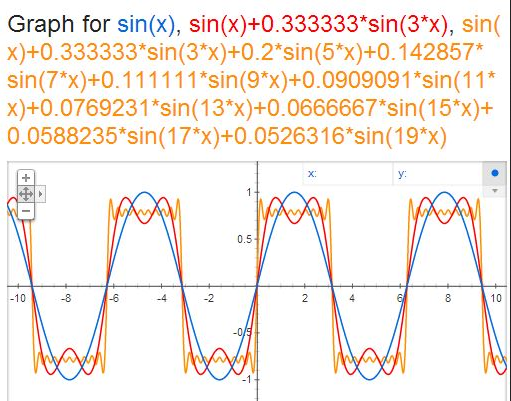Gambar 3. sumber gambar: [1]
Ada tiga buah gelombang yang berbeda pada Gambar 3. Bisa kita lihat akibat dari penggabungan sejumlah gelombang yang berbeda frekuensi dan amplitudonya pada satu gelombang. Dengan pengaturan tertentu, kita bisa melihat bahwa gelombang ketiga yang merupakan gelombang hasil gabungan dari beberapa gelombang sudah menyerupai bentuk dari gelombang kotak.
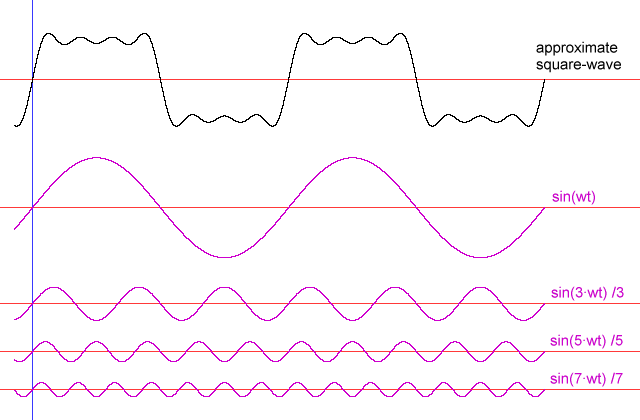Gambar 4. sumber gambar: [2]
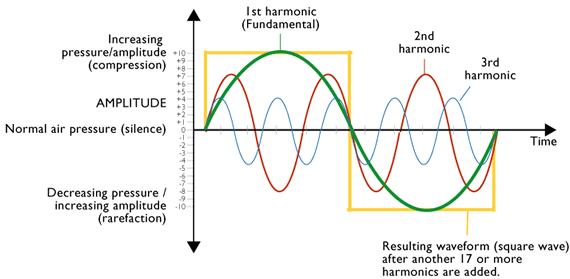
Atau kalau kita mencoba melihat dari sudut yang berbeda (arah datang yang lain) maka kita bisa mengatakan bahwa sebuah gelombang “yang menyerupai gelombang segi empat” dapat diuraikan menjadi beberapa gelombang sinusoida yang memiliki besar (amplitudo) dan frekuensi tertentu seperti terlihat pada Gambar 4.
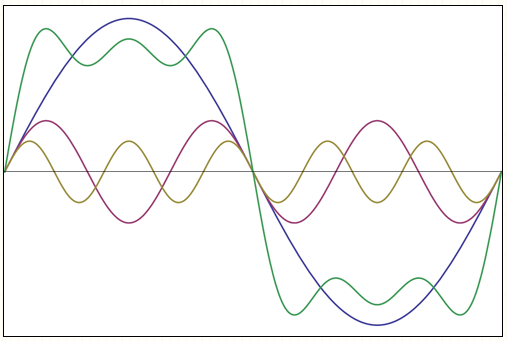Gambar 5. sumber gambar: [2]
Bentuk gelombang serupa dengan gelombang terakhir pada Gambar 3 bisa ditampilkan terpisah agar lebih jelas seperti pada Gambar 5. Tiga buah gelombang sinus membentuk gelombang yang mendekati bentuk segi empat yang diberi warna hijau.
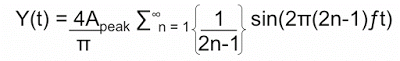Gambar 6. Persamaamaan dasar pembentukan gelombang segi empat (w/harmonics)
sumber gambar: [3]
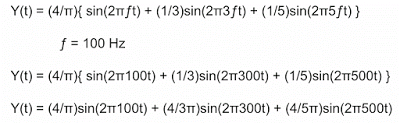Gambar 7. Contoh pengerjaan untuk frekuensi dasar 100 Hz
sumber gambar: [3]
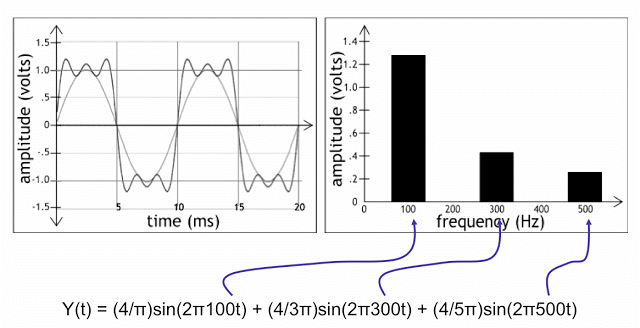Gambar 8. Gelombang segi empat yang dibentuk/terdiri dari tiga harmonics
sumber gambar: [3]
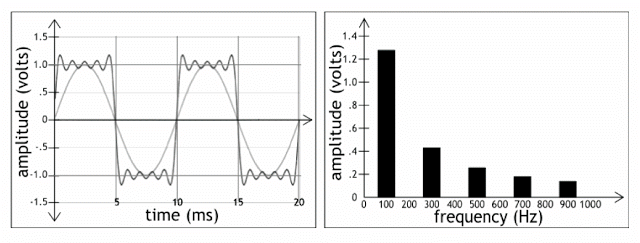Gambar 9. Gelombang segi empat yang dibentuk/terdiri dari lima harmonics
sumber gambar: [3]
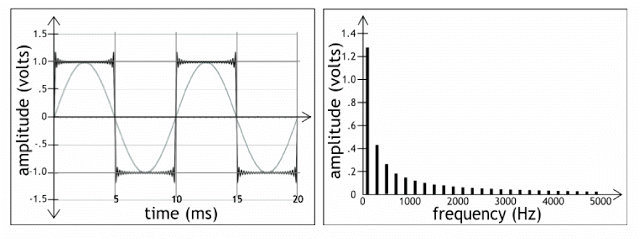Gambar 10. Gelombang segi empat yang dibentuk/terdiri dari dua puluh lima harmonics
sumber gambar: [3]
Sebuah gelombang kotak (segi empat) yang “sempurna” dapat dibentuk jika kita memiliki lebar pita harmonisa (harmonics) yang tidak terbatas. Dengan kata lain suatu gelombang yang semakin mendekati bentuk gelombang kotak maka akan semakin memiliki banyak harmonics.
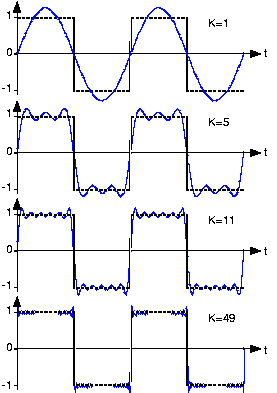
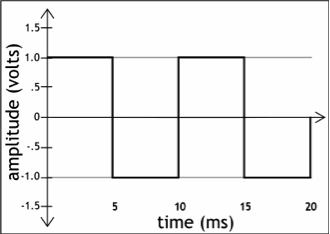Gambar 11. sumber gambar: [3]
Bandingkan antara Gambar 11 dengan Gambar 12 berikut ini.
Gambar 12. sumber gambar: [2]
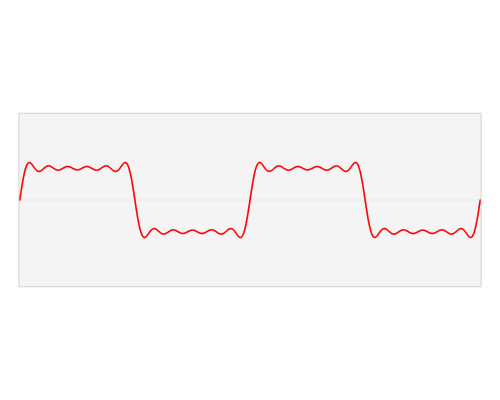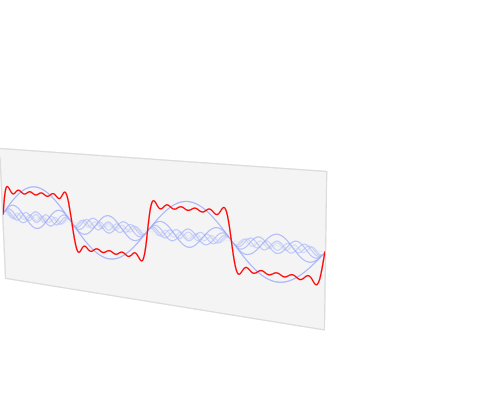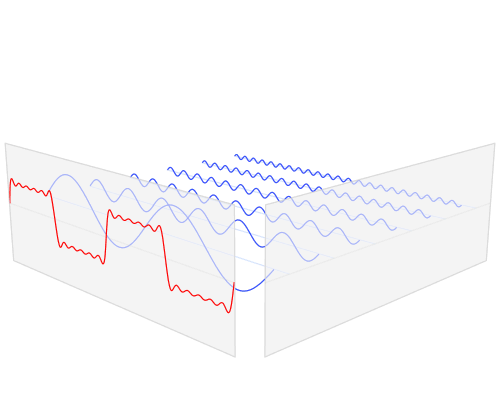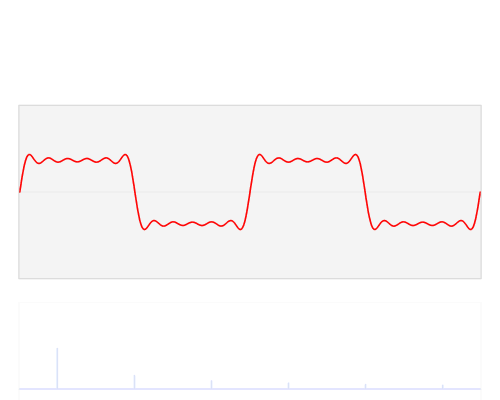Gambar 13. Visualisasi 3D untuk kawasan waktu dan kawasan frekuensi
sumber gambar: [2]
Gambar 14. sumber gambar: [4]
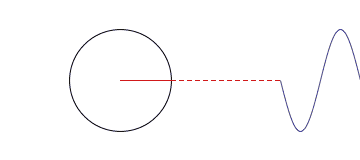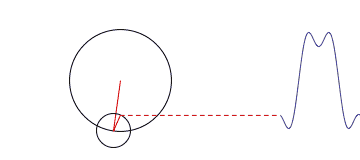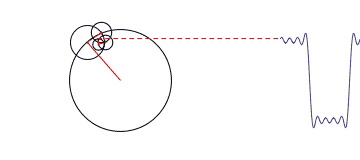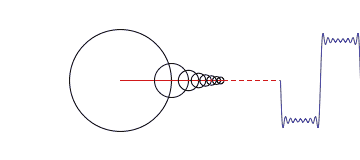
Gambar 15. sumber: http://rebloggy.com/
The smooth motion of rotating circles can be used to build up any repeating curve even one as angular as a digital square wave. Each circle spins at a multiple of a fundamental frequency, and a method called Fourier analysisshows how to pick the radiuses of the circles to make the picture work.Decomposing signals like this lies at the heart of a lot of signal processing.
REFERENSI:
[01] https://georgemdallas.wordpress.com/2014/05/14/wavelets-4-dummies-signal-processing-fourier-transforms-and-heisenberg/[02] http://electronics.stackexchange.com/questions/32310/what-exactly-are-harmonics-and-how-do-they-appear
[03] http://recordingology.com/in-the-studio/distortion/square-wave-calculations/
[04] http://www.planetoftunes.com/sound-audio-theory/complex-soundwaves.html#.Vf69131GSPc
[05] https://www.falstad.com/fourier/
[06] https://www.mathworks.com/help/matlab/math/square-wave-from-sine-waves.html
[07] http://sage.brandoncurtis.com/fourier.html
[08] http://controlsystemsacademy.com/0018/0018.html
[09] https://www.intmath.com/fourier-series/fourier-graph-applet.php
[10] https://phet.colorado.edu/en/simulations/fourier
[11] https://www.jezzamon.com/fourier/
[12] https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
[13] https://www.cytechglobal.com/products/analog-devices/technical-articles/try-ltspice/try-ltspice-frequency-analysis-using-fft