Pada post sebelumnya telah diungkapkan uji coba penggunaan Scilab untuk perhitungan numeris average (mean) dan RMS untuk gelombang sinus. Sedangkan perhitungan simbolik untuk menurunkan persamaan average dan RMS gelombang sinus dipergunakan Maxima, yang telah juga saya ungkap di post yang lain. Persamaan-persamaan ini bisa dibuktikan dengan percobaan menggunakan komponen hardware, dibantu dengan simulasi sebagai pembanding [link].
Pada post ini akan diungkapkan ulang mengenai penggunaan Scilab dengan fungsi. Juga sekaligus beberapa cara lain untuk menghitung hal yang sama yang pernah diungkap di post sebelumnya.
 Gambar 1.
Gambar 1.
[su_panel border=”2px solid #7FFF81″ shadow=”1px 2px 2px #7FFF81″ radius=”10″]
Pada bagian pertama ini percobaan penggunaan Scilab dimulai dari bentuk yang sederhana. Persamaan untuk mencari nilai RMS dari gelombang sinus dilakukan dengan pengaturan bahwa nilai amplitudonya (A_in) tetap yaitu bernilai satu.
Di bagian ini, sama seperti pada post terdahulu, kembali akan dimulai dengan penggunaan fungsi sqrt dan integrate.
clear;
clc;
A_in=1;
A_rms= A_in * sqrt((1/(2*%pi))*integrate('(sin(x))^2','x',0,(2*%pi)))
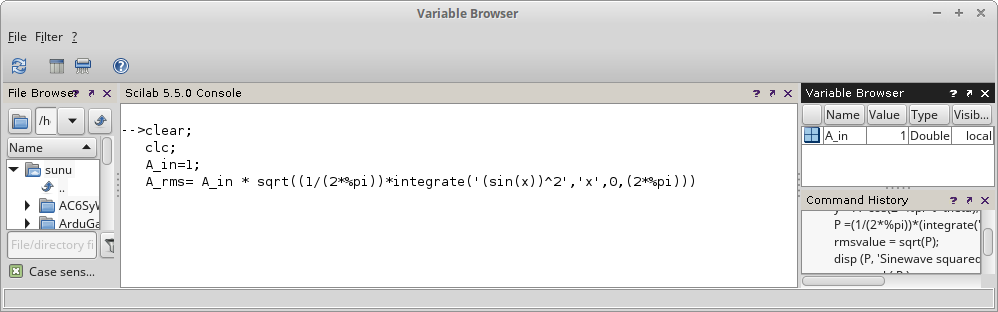 Gambar 2.
Gambar 2.
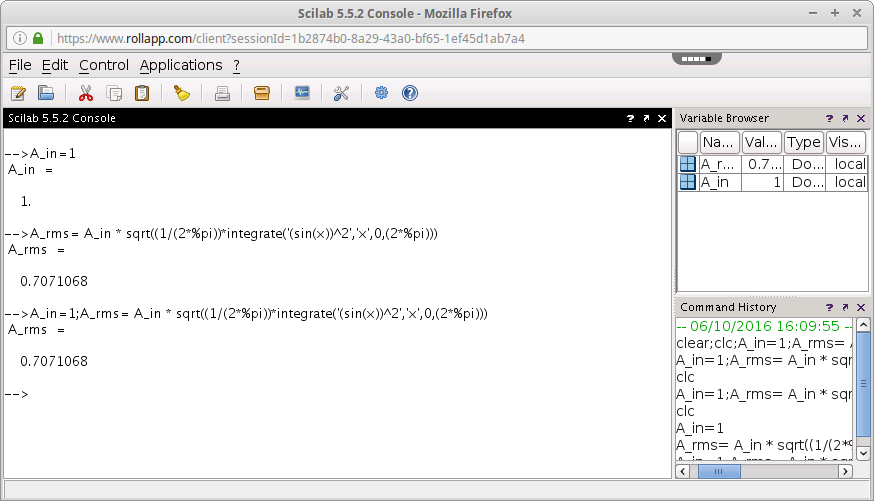 Gambar 3. Hasil perhitungan.
Gambar 3. Hasil perhitungan.
Pada Gambar 3, dapat dilihat hasil perhitungan numerik untuk mencari nilai RMS gelombang sinus.
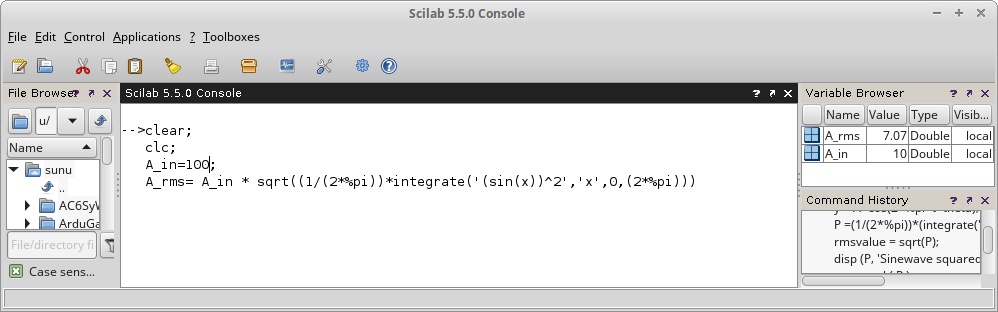 Gambar 4. Nilai A_in diganti menjadi 100.
Gambar 4. Nilai A_in diganti menjadi 100.
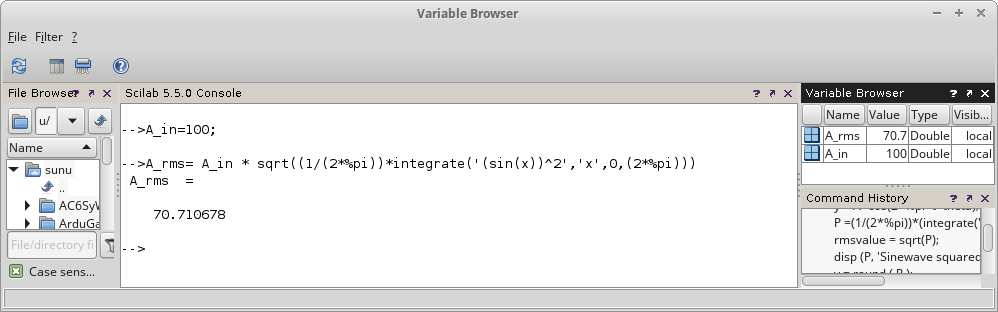 Gambar 5. Hasil perhitungan, nilai A_rms.
Gambar 5. Hasil perhitungan, nilai A_rms.
[/su_panel]
[su_panel border=”2px solid #FF6473″ shadow=”1px 2px 2px #D95562″ radius=”10″]
function [coef1,A_rms]=hitungRMS(A_in)
coef1=sqrt((1/(2*%pi))*integrate('(sin(x))^2','x',0,(2*%pi)))
A_rms=coef1*A_in
endfunction
Contoh salah:
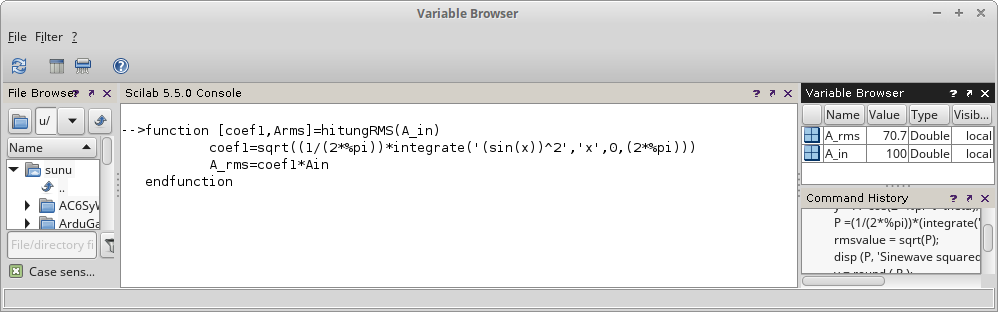 Gambar 6.
Gambar 6.
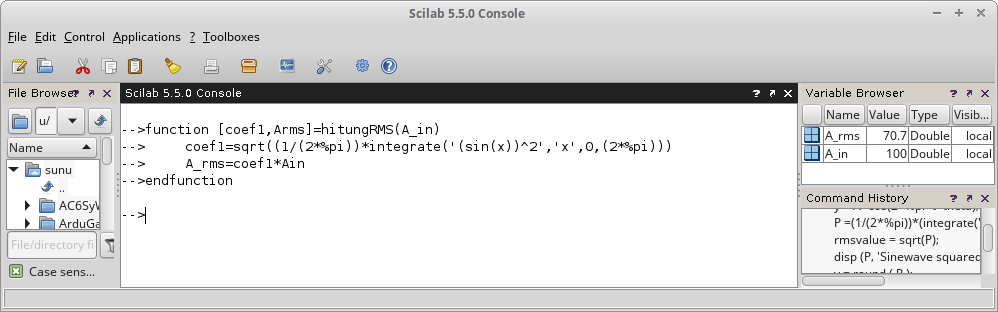 Gambar 7.
Gambar 7.
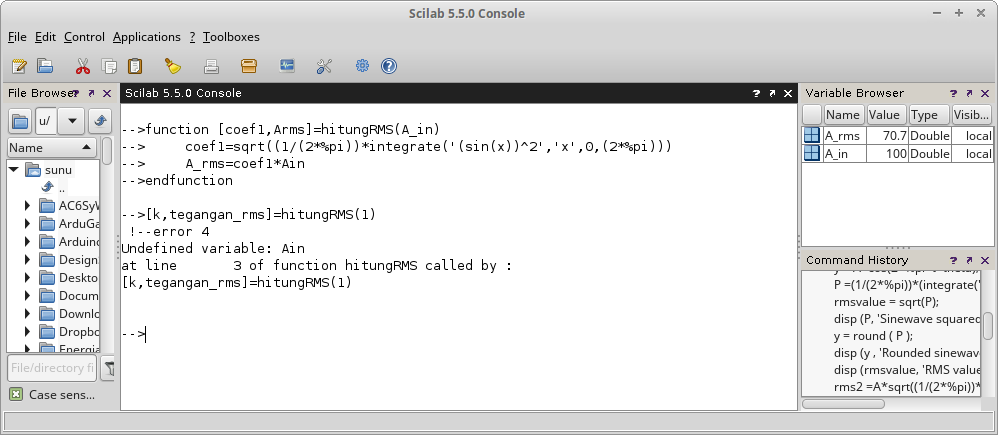 Gambar 8.
Gambar 8.
Perhatikan penyebab sehingga Scilab menampilkan pesan kesalahan pada Gambar 8.
Contoh benar:
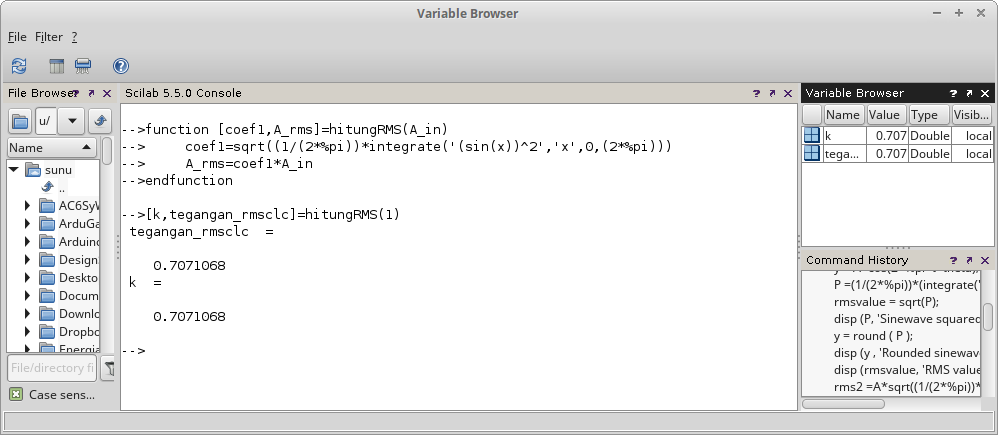 Gambar 9. Penampilan hasil perhitungan dalam matrix.
Gambar 9. Penampilan hasil perhitungan dalam matrix.
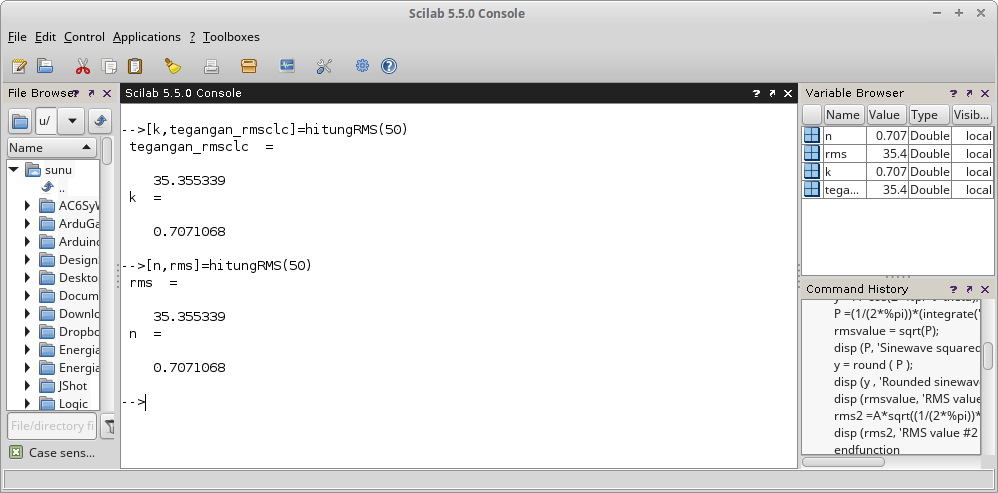 Gambar 10. Penamaan matrix pada pemanggilan fungsi.
Gambar 10. Penamaan matrix pada pemanggilan fungsi.
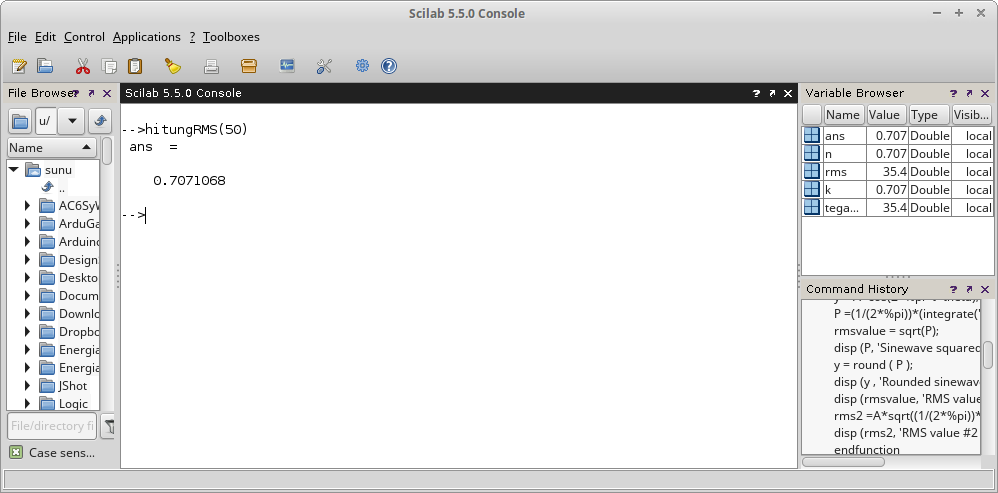 Gambar 11. Pemanggilan fungsi tanpa menyediakan matrix untuk hasil.
Gambar 11. Pemanggilan fungsi tanpa menyediakan matrix untuk hasil.
[/su_panel]
[su_panel border=”2px solid #65E6FF” shadow=”1px 2px 2px #65E6FF” radius=”10″]
Penggunaan fungsi linspace dan mean.
function Arms=hitungRMSv2(Ain,divr)
x=linspace(0,2*%pi,divr)
y=sin(x)
Arms=Ain*sqrt(mean(y.^2))
endfunction
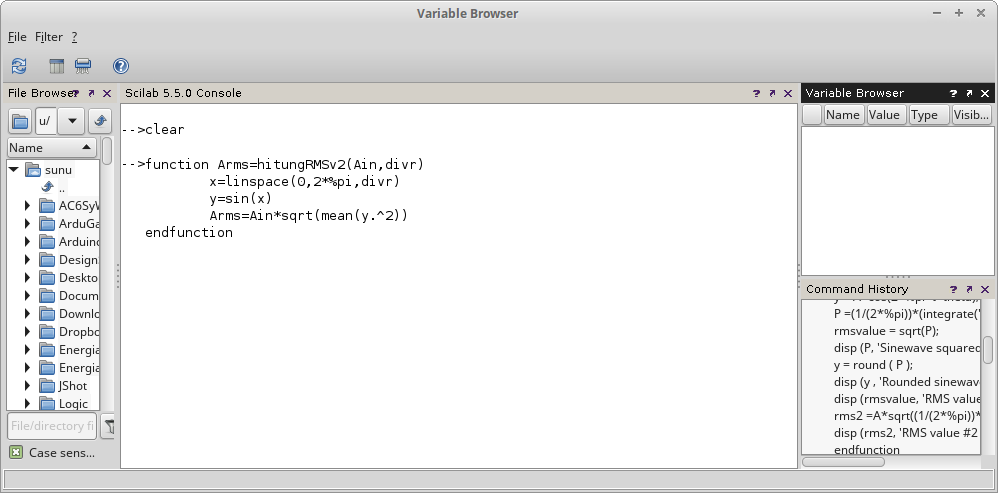 Gambar 12.
Gambar 12.
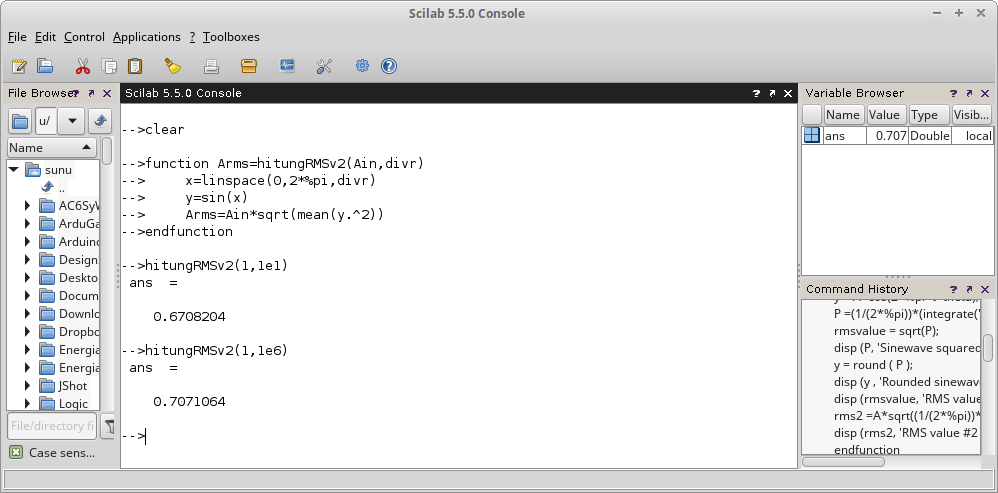 Gambar 13.
Gambar 13.
[/su_panel]
[su_panel border=”2px solid #A46D00″ shadow=”1px 2px 2px #A46D00″ radius=”10″]
Fungsi disp.
function Arms=hitungRMSv2(Ain,divr)
x=linspace(0,2*%pi,divr)
y=sin(x)
Arms=Ain*sqrt(mean(y.^2))
disp (Arms, 'Nilai RMS dari Amplitudo yang anda masukkan')
endfunction
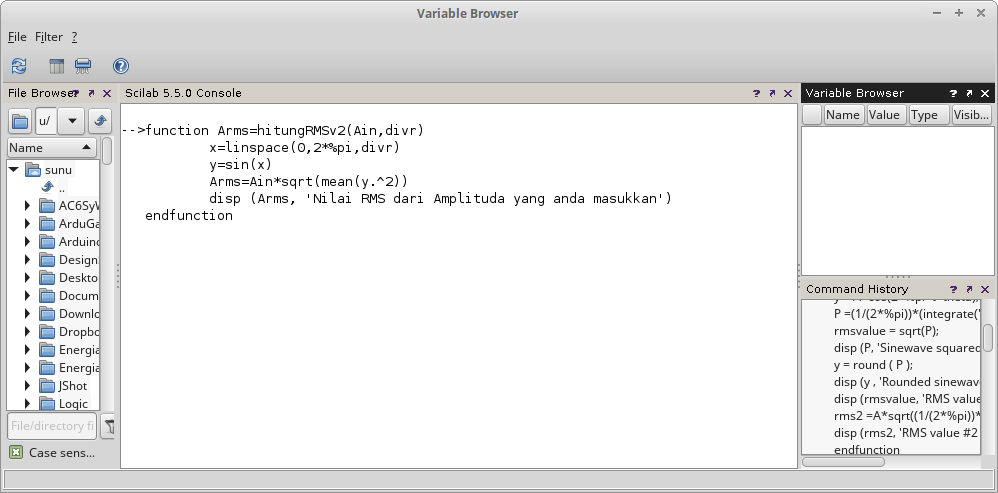 Gambar 14.
Gambar 14.
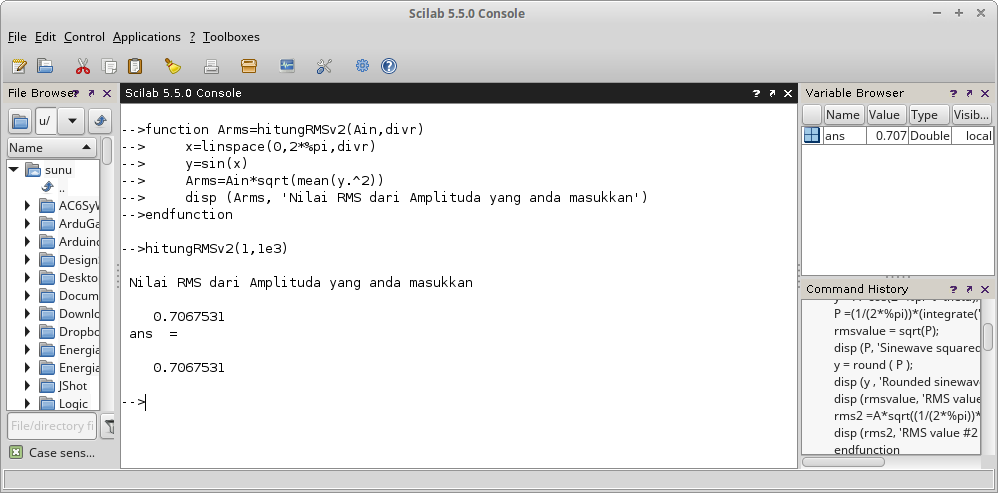 Gambar 15.
Gambar 15.
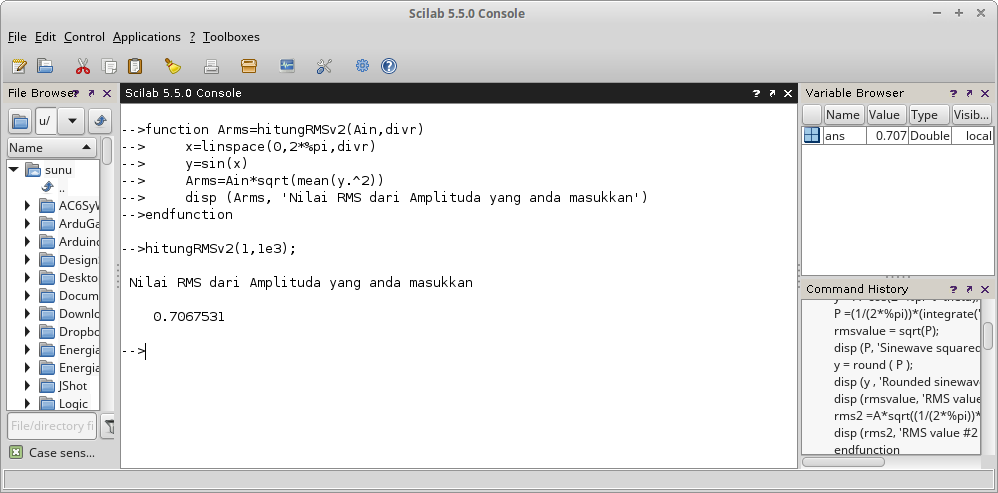 Gambar 16.
Gambar 16.
[/su_panel]
[su_panel border=”2px solid #D1FF8C” shadow=”1px 2px 2px #D1FF8C” radius=”10″]
clear; clc; function y = f(x), y = x + 1, endfunction
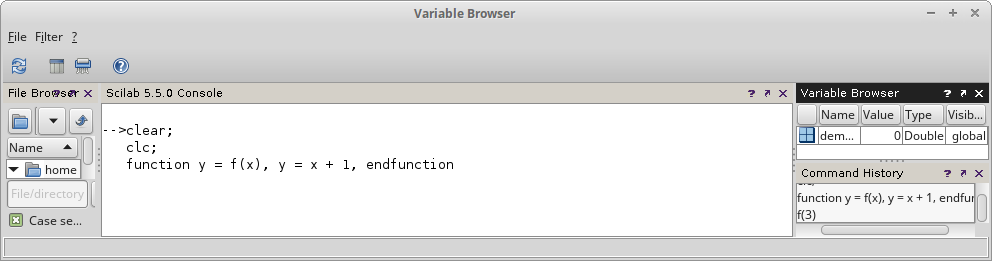 Gambar 17.
Gambar 17.
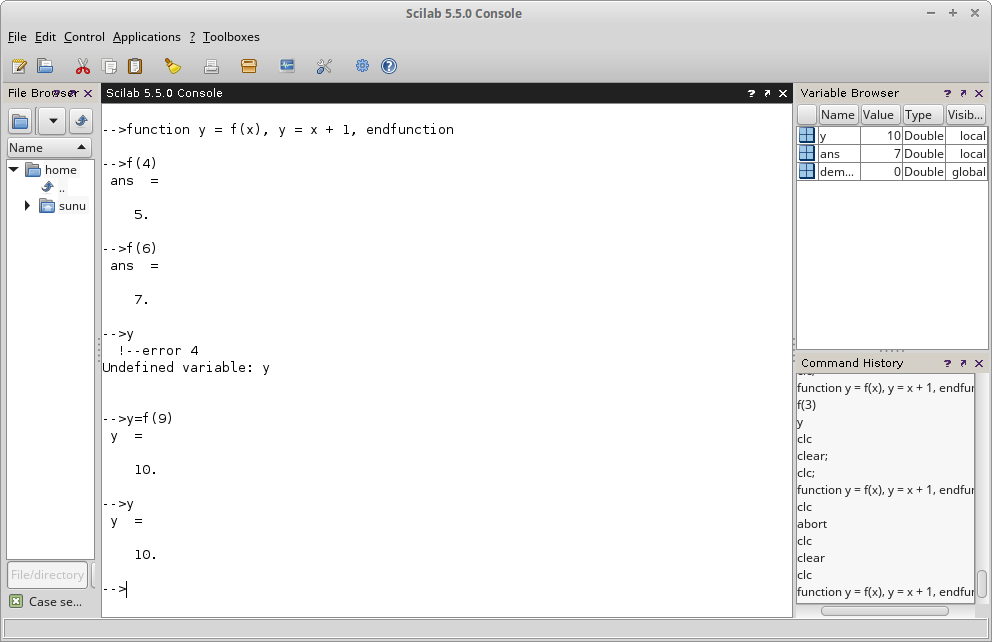 Gambar 18.
Gambar 18.
clear; clc; function j = d(w), j = w + 1, endfunction
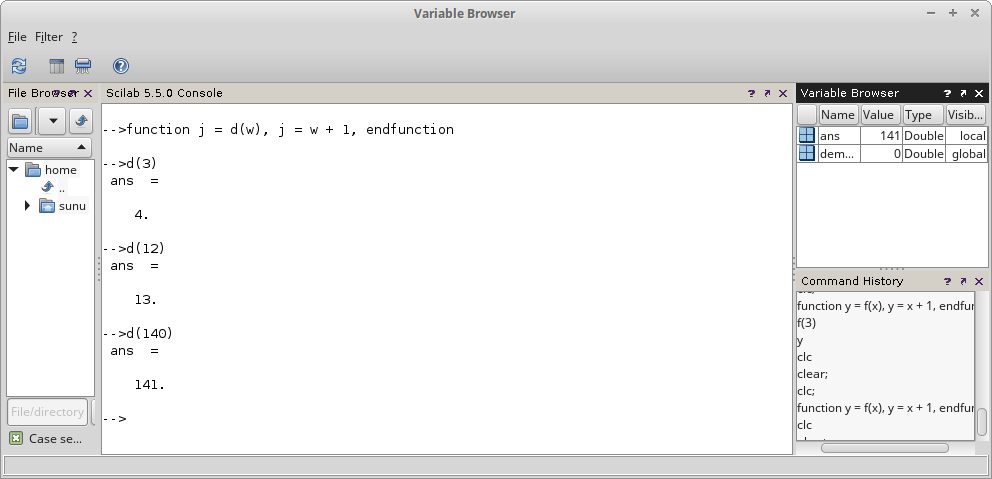 Gambar 19.
Gambar 19.
clear; clc; function j = d(w), j = w + 1, endfunction A1=d(3)^2 A2=d(4)^2 A3=d(5)^2
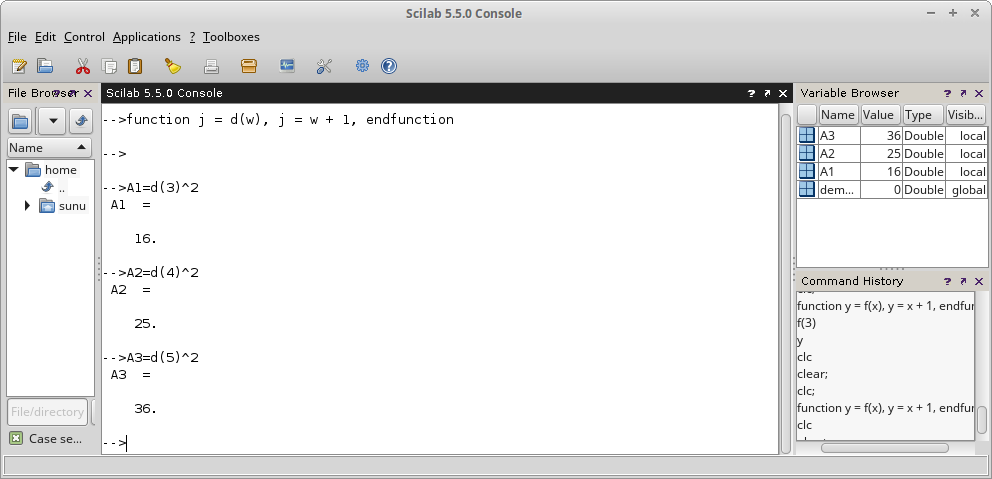 Gambar 20.
Gambar 20.
clear; clc; function y = f(x), y = (sin(x))^2, endfunction rms = sqrt( (1/(2*%pi)) * intg(0, 2*%pi, f))
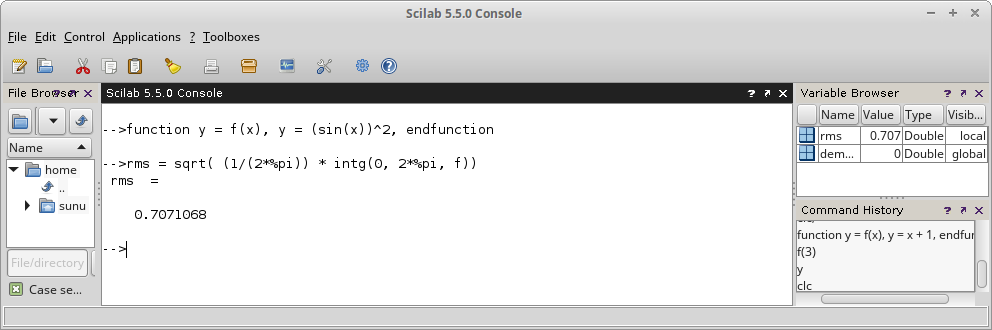 Gambar 21.
Gambar 21.
clear;
clc;
function y = f(x), y = (sin(x))^2, endfunction
rms = sqrt( (1/(2*%pi)) * intg(0, 2*%pi, f));
printf("Nilai rms adalah : " + string(rms));
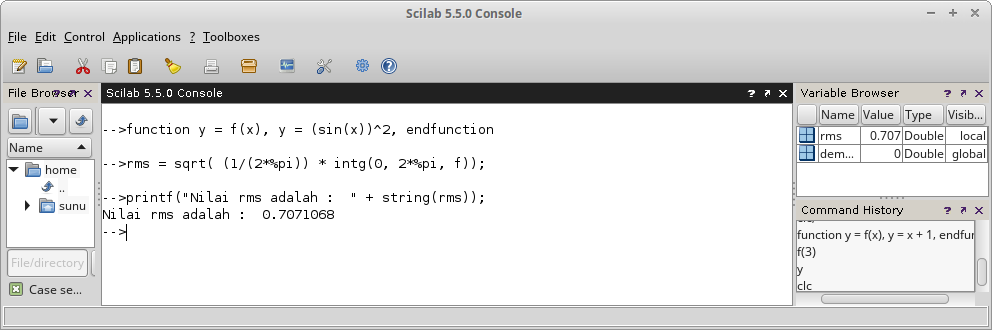 Gambar 22.
Gambar 22.
Fungsi printf.
clear;
clc;
function y = f(x)
y = (sin(x))^2
endfunction
rms = sqrt( (1/(2*%pi)) * intg(0, 2*%pi, f))
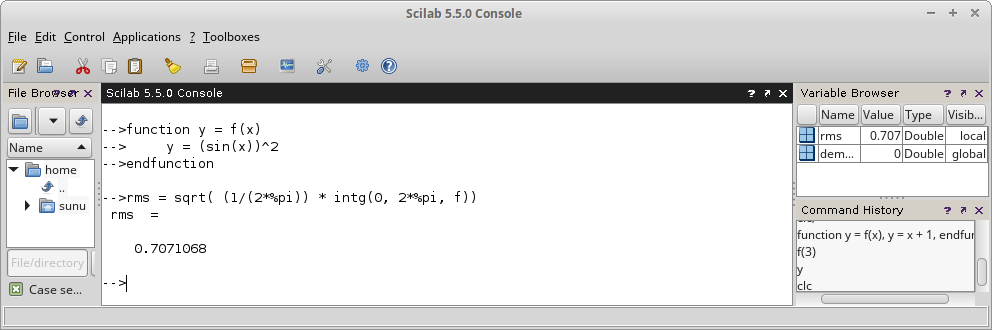 Gambar 23.
Gambar 23.
Fungsi intg.
clear;
clc;
function y = f(x)
y = (sin(x))^2
endfunction
function hitungRMS(Ain)
rmsNum = sqrt( (1/(2*%pi)) * intg(0, 2*%pi, f));
rms = Ain * rmsNum;
disp(rms,"Nilai rms dari sinyal masukan: ")
endfunction
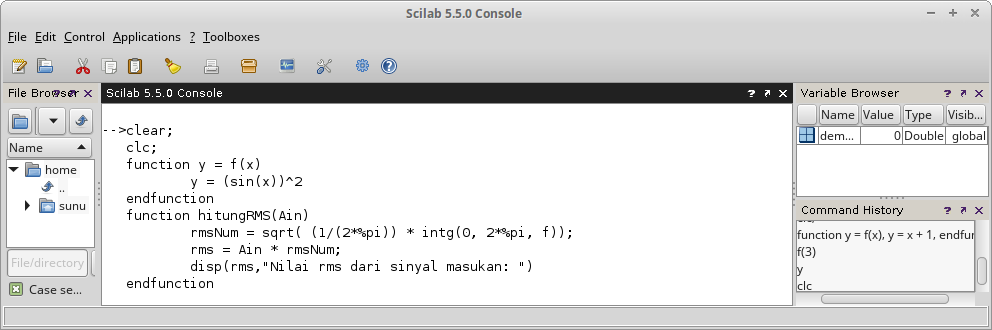 Gambar 24.
Gambar 24.
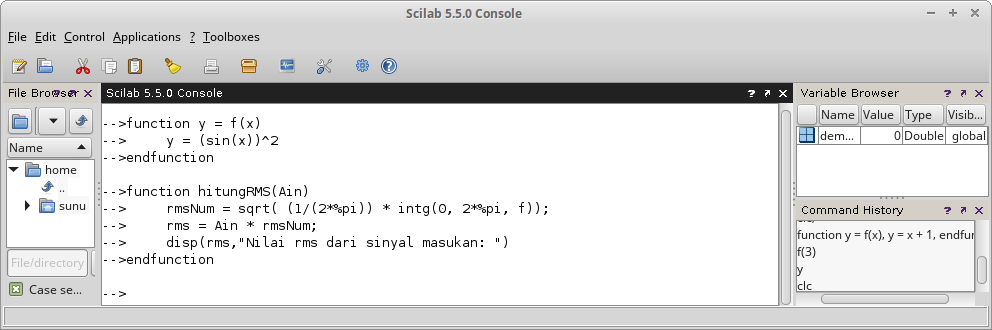 Gambar 25.
Gambar 25.
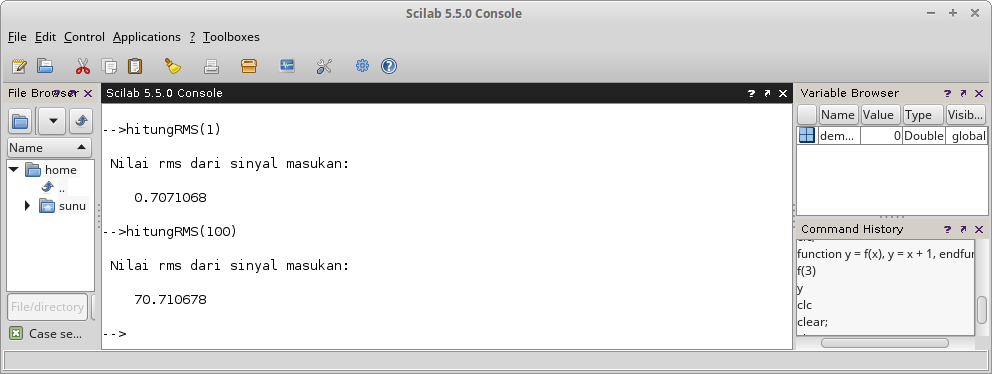 Gambar 26.
Gambar 26.
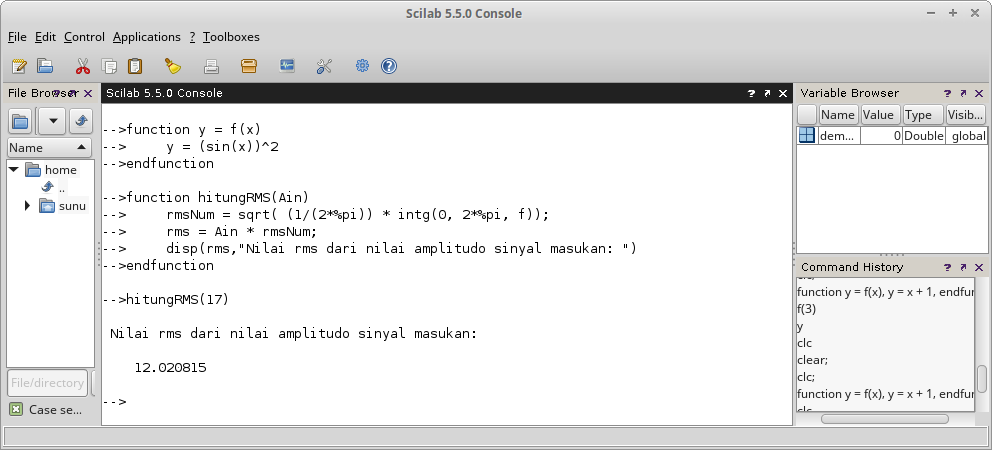 Gambar 27.
Gambar 27.
clear;
clc;
function y = f(x)
y = (sin(x))^2
endfunction
function hitungPeak(rms_in)
rmsNum = sqrt( (1/(2*%pi)) * intg(0, 2*%pi, f));
S_peak = rms_in / rmsNum;
disp(S_peak,"Nilai amplitudo dari masukan rms : ")
endfunction
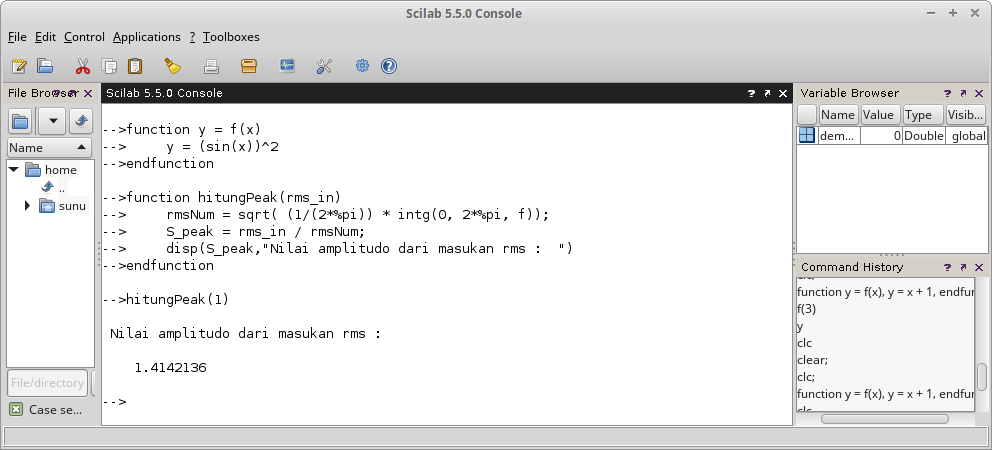 Gambar 28.
Gambar 28.
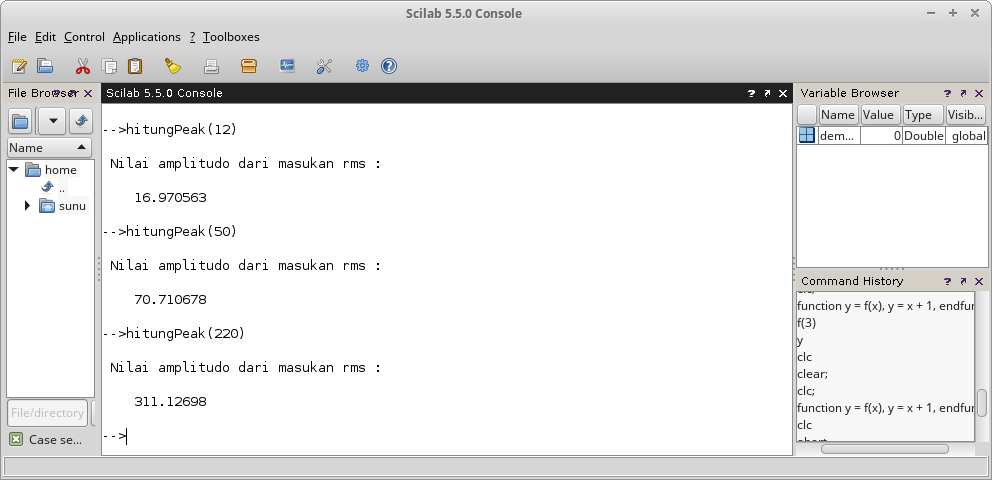 Gambar 29.
Gambar 29.
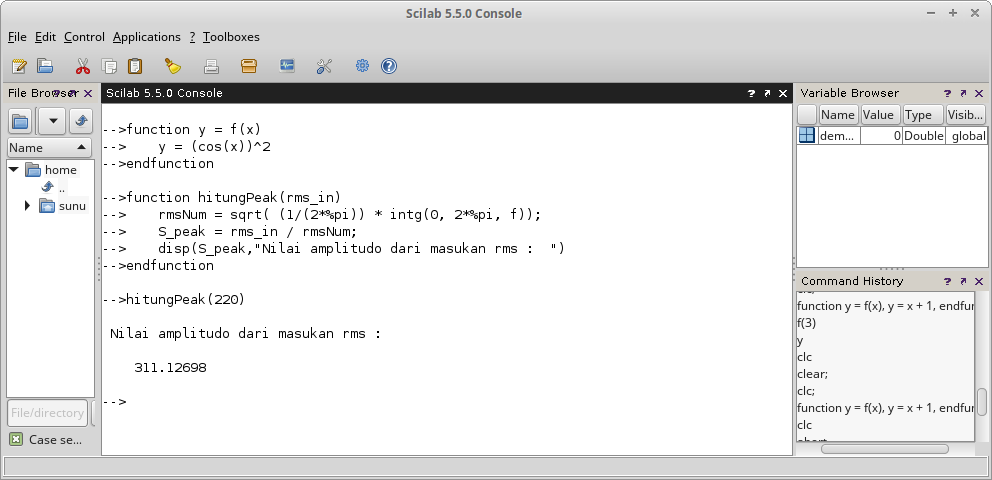 Gambar 30.
Gambar 30.
[/su_panel]
[su_panel border=”2px solid #C5BB4A” shadow=”1px 2px 2px #C5BB4A” radius=”10″]
function sunu_rms
// clear;
clc ;
A = 1;
x =0:1:10;
sig =(integrate('A^2*(sin(x))^2','x',0,2*%pi))/(2*%pi);
disp (sig, 'Kuadrat dari sinyal adalah : ');
y2 = round (sig);
disp (y2 , 'Pembulatan nilai kuadrat dari sinyal adalah:');
A_rms=sqrt(sig);
disp (A_rms , 'Nilai RMS (cara #1) dari sinyal adalah:');
A_rms=A* sqrt((integrate('(sin(x))^2','x',0,2*%pi))/(2*%pi));
disp (A_rms , 'Nilai RMS (cara #2) dari sinyal adalah:');
A_rms=sqrt((integrate('(A*(sin(x)))^2','x',0,2*%pi))/(2*%pi));
disp (A_rms , 'Nilai RMS (cara #3) dari sinyal adalah:');
A_rms=sqrt((integrate('A^2*(cos(x))^2','x',0,2*%pi))/(2*%pi));
disp (A_rms , 'Nilai RMS (cara #4) dari sinyal adalah:');
endfunction
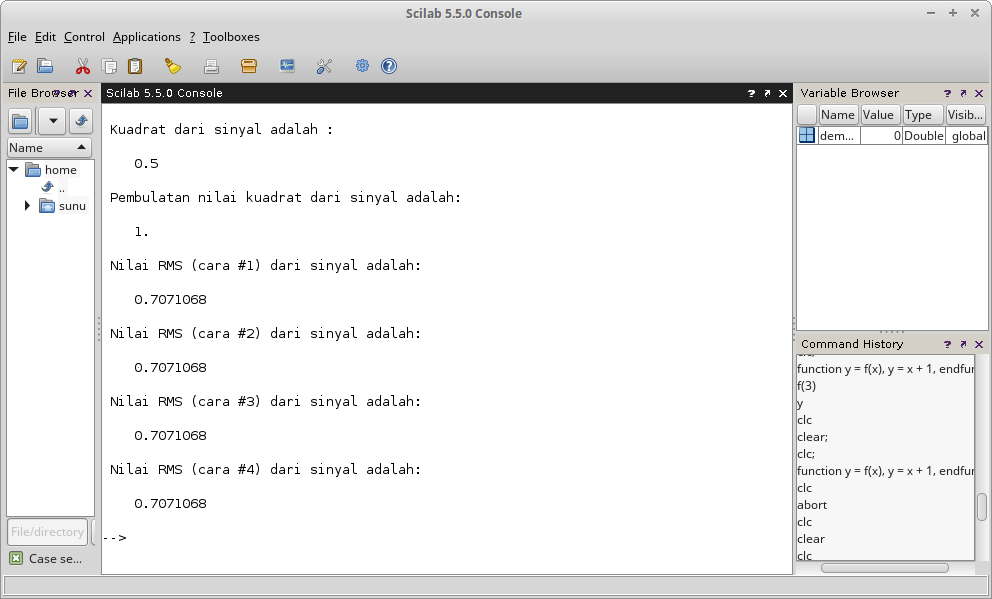 Gambar 31.
Gambar 31.
[/su_panel]
[su_panel border=”2px solid #CCFF33″ shadow=”1px 2px 2px #CCFF33″ radius=”10″]
\(y = A\times \sin \left ( x+\theta \right )\)
clear;
clc;
function plotSig(Ain,res,end)
//clc;
A = Ain;
f = 1;
theta = 0;
x = 0:res:end;
y = A*sin((x)+theta);
plot(x,y)
endfunction
plotSig(1,1e-3,2*%pi)
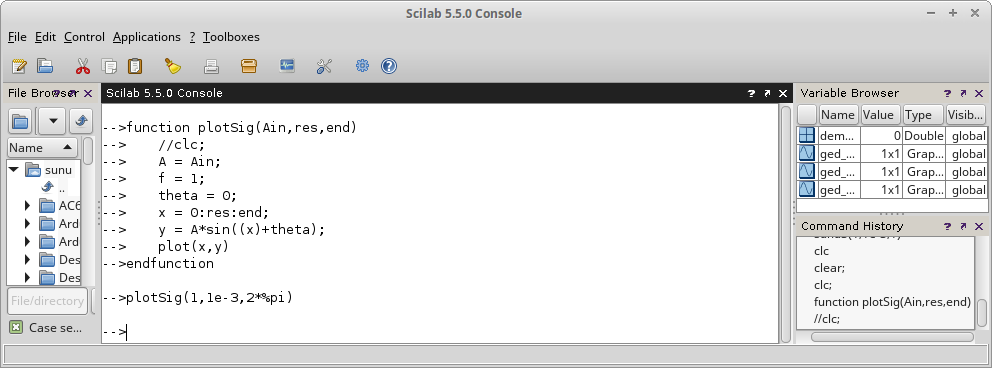 Gambar 32.
Gambar 32.
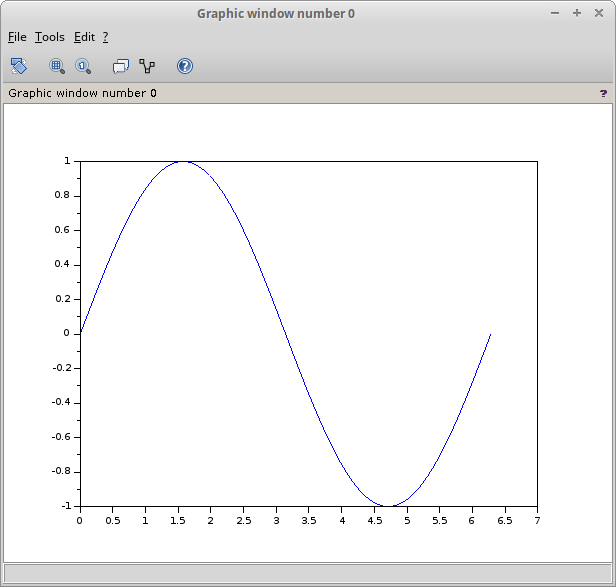 Gambar 33.
Gambar 33.
\(y = A \times \sin \left ( \left (2\times \pi \times f \times t \right ) + \theta \right )\)
clear; clc; function plotSig(Ain,res,end) //clc; A = Ain; f = 1; theta = 0; x = 0:res:end; y = A*sin((2*%pi*f*x)+theta); plot(x,y) endfunction plotSig(1,1e-3,1)
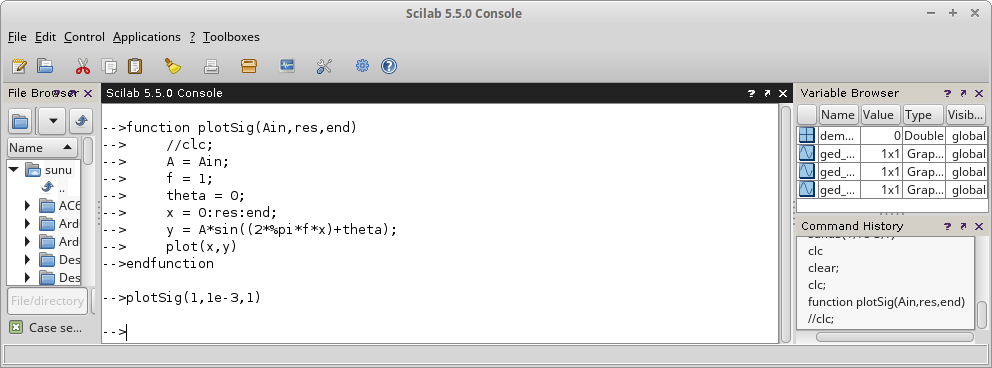 Gambar 34.
Gambar 34.
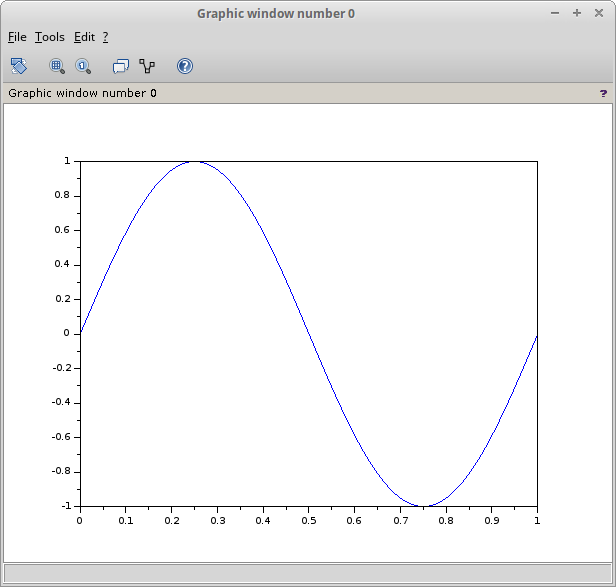 Gambar 35.
Gambar 35.
[/su_panel]
[su_panel border=”2px solid #FF3300″ shadow=”1px 2px 2px #FF3300″ radius=”10″]
clear;
clc;
function A_sesaat(Ain,t,thetaRad)
//clc;
y = Ain*sin((t)+thetaRad);
disp(y,"Nilai amplitudo")
endfunction
A_sesaat(1,1.57,0)
A_sesaat(1, (1/4)*(2*%pi) ,0)
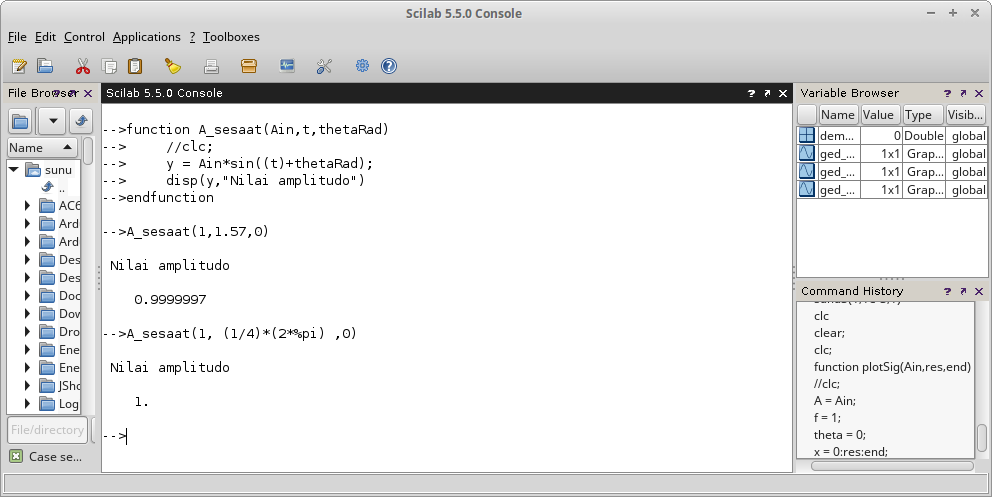 Gambar 36.
Gambar 36.
clear;
clc;
function A_sesaat(Ain,f,t,thetaRad)
//clc;
y = Ain*sin((2*%pi*f*t)+thetaRad);
disp(y,"Nilai amplitudo")
endfunction
A_sesaat(1,50,0.005,0)
A_sesaat(1,50, asin(1)/(2*%pi*50) ,0)
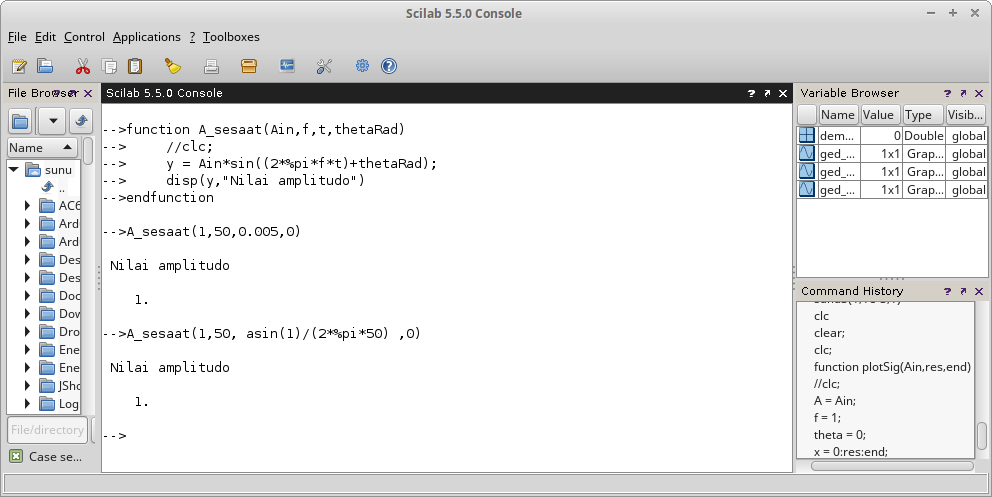 Gambar 37.
Gambar 37.
[/su_panel]
[su_panel border=”2px solid #9900FF” shadow=”1px 2px 2px #8900E5″ radius=”10″]
Contoh penggunaan fungsi intsplin.
clc t=0:1e-1:2*%pi; sqrt((1/(2*%pi))*intsplin(t,sin(t).^2)) t=0:1e-3:2*%pi; sqrt((1/(2*%pi))*intsplin(t,sin(t).^2))
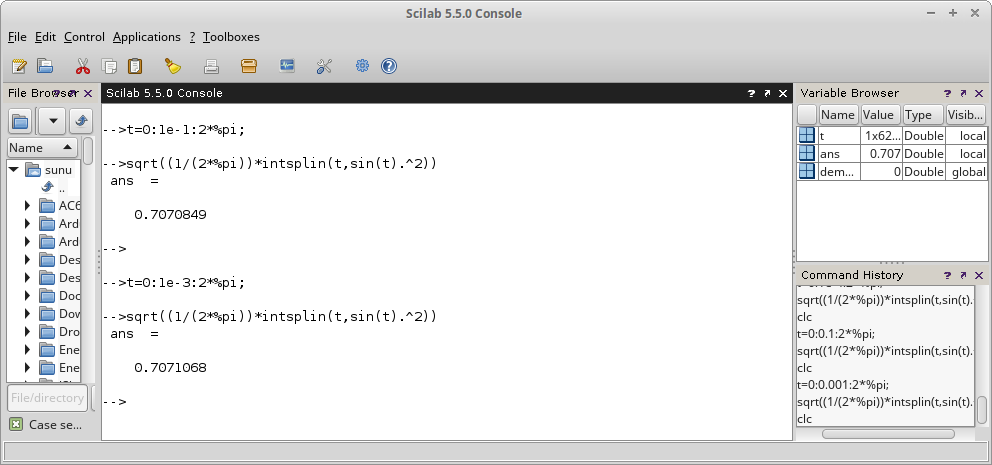 Gambar 38.
Gambar 38.
[/su_panel]
[su_panel border=”2px solid #80B3FF” shadow=”1px 2px 2px #80B3FF” radius=”10″]
Semua perhitungan yang menggunakan fungsi sin maupun cos dalam Scilab dihitung dalam radian. Sedangkan untuk mode derajat (degree) fungsi yang dipegunakan adalah sind dan cosd.
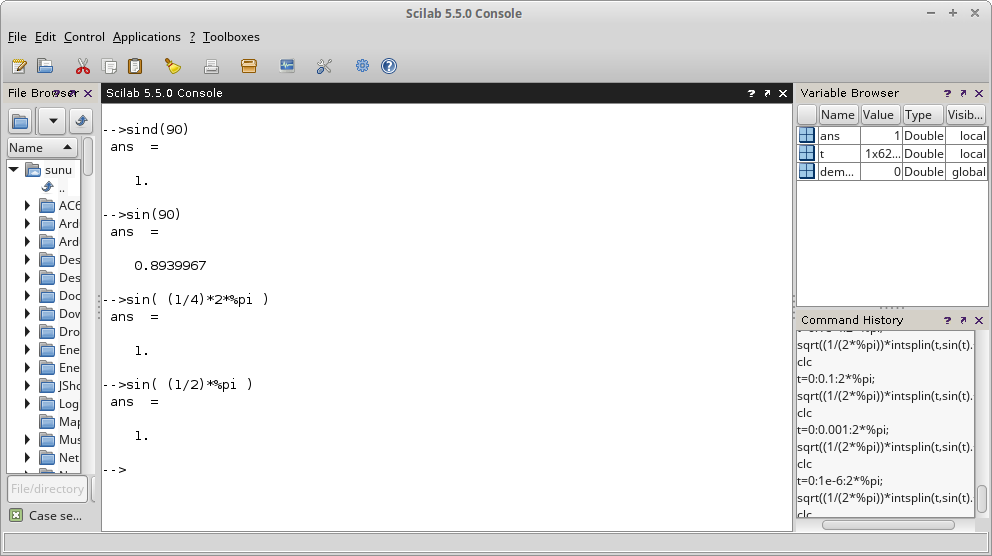 Gambar 39. [/su_panel]
Gambar 39. [/su_panel]
[su_panel border=”2px solid #FF33CC” radius=”10″]
[/su_panel]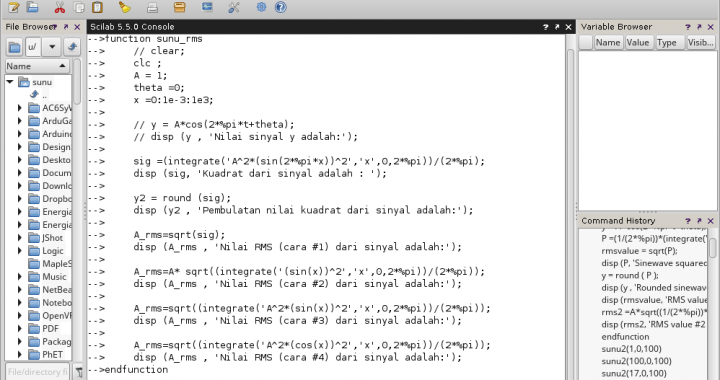


 Gambar 1.
Gambar 1.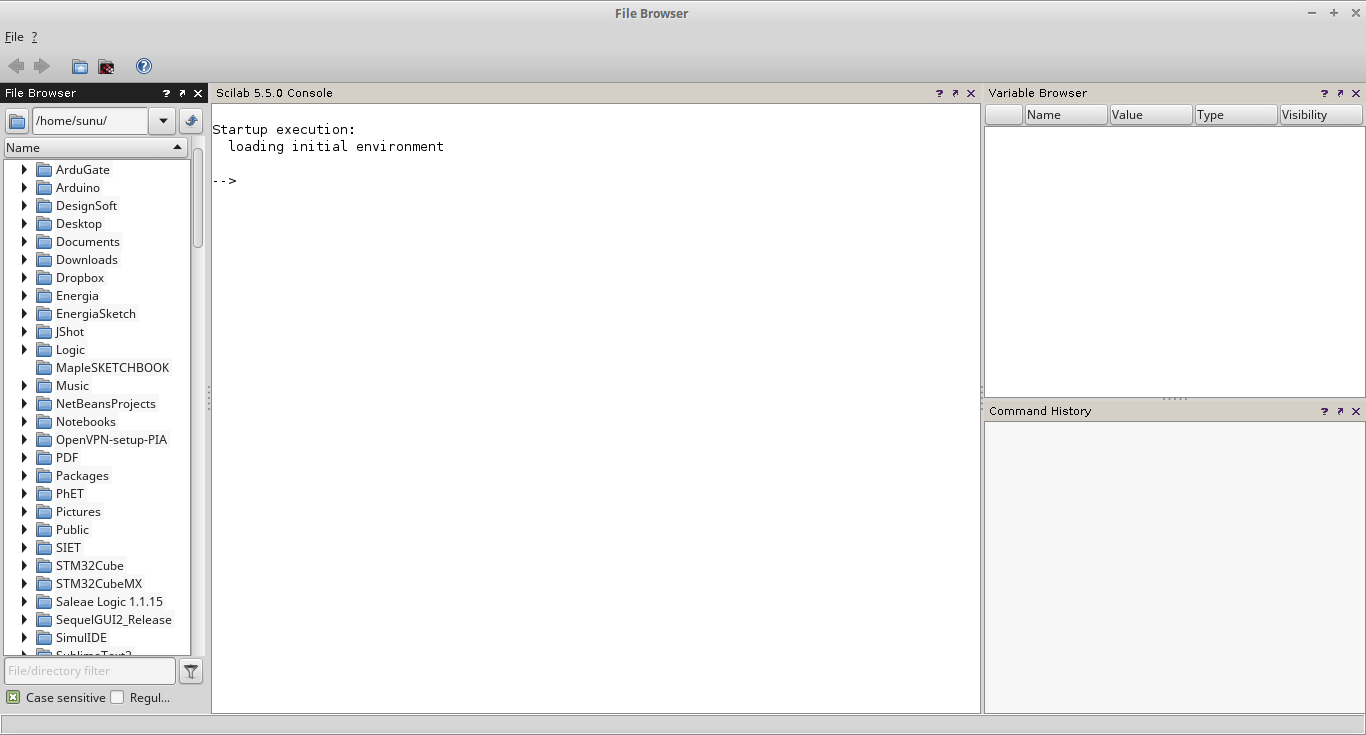 Gambar 2. Scilab (offline) di sistem GNU/Linux.
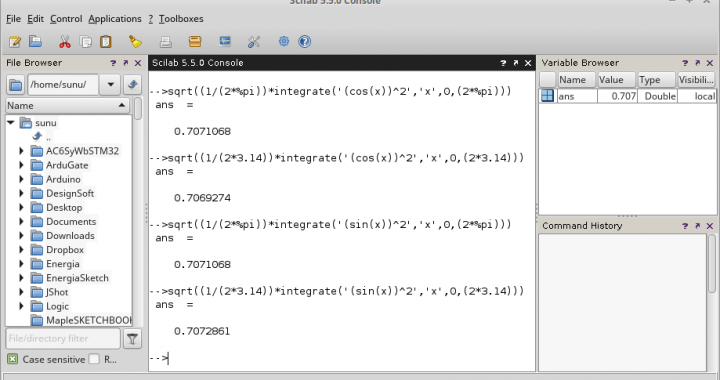
Gambar 2. Scilab (offline) di sistem GNU/Linux.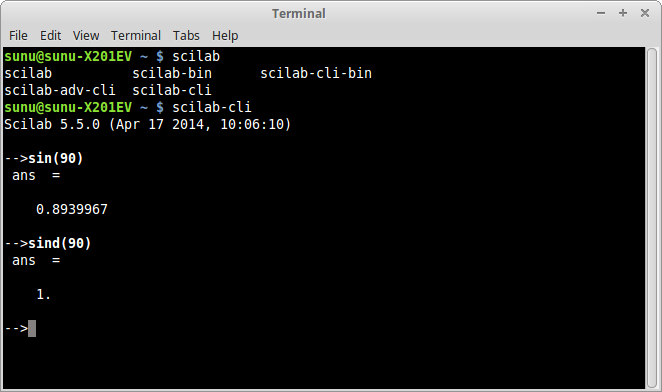 Gambar 3. Scilab-cli (offline) di sistem GNU/Linux.
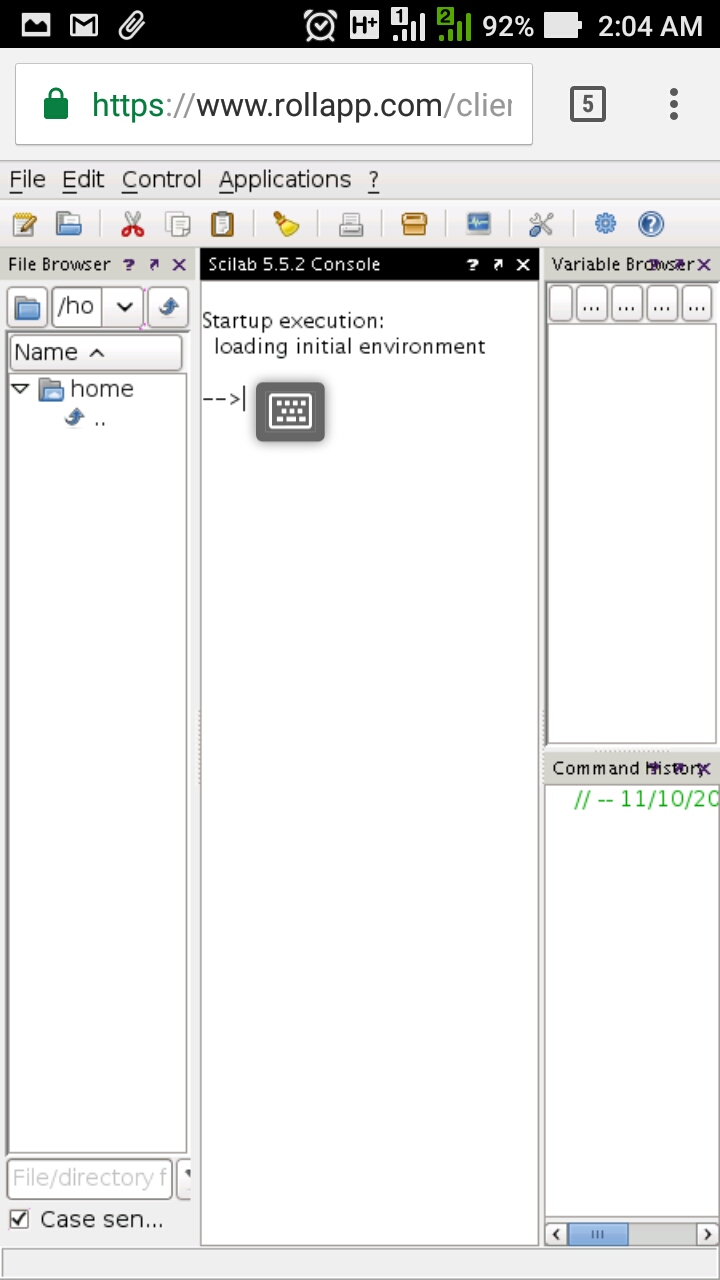
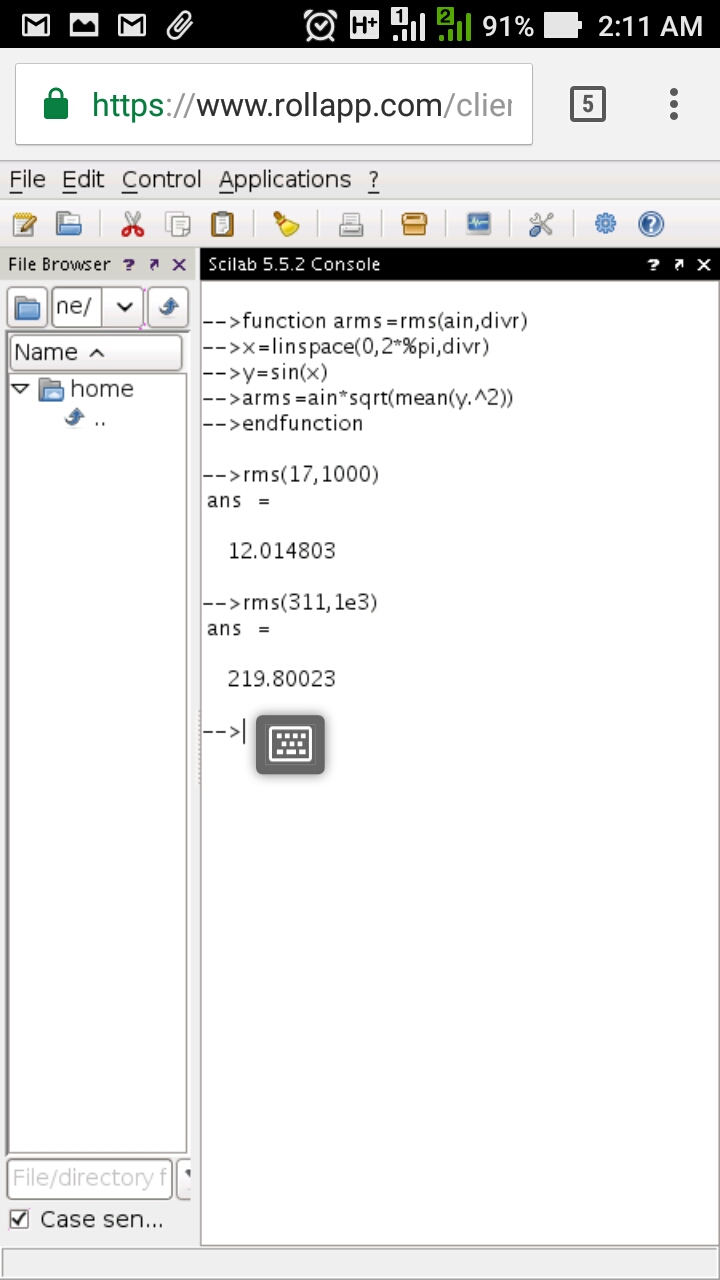
Gambar 3. Scilab-cli (offline) di sistem GNU/Linux.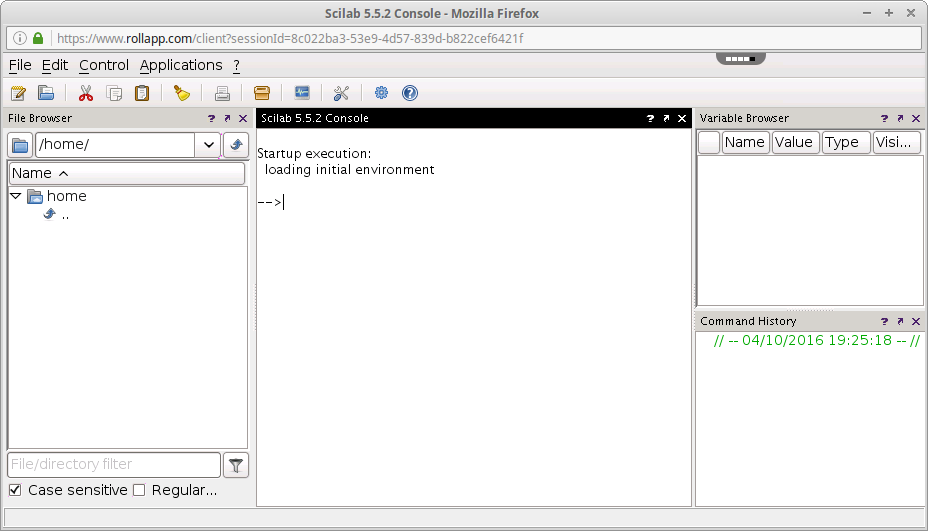 Gambar 4. Scilab (online) di rollApp.
Gambar 4. Scilab (online) di rollApp.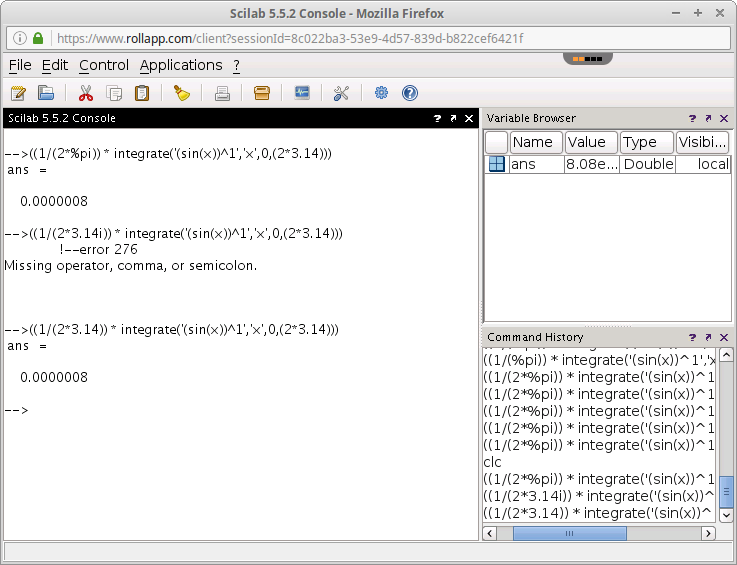 Gambar 5.
Gambar 5. Gambar 6. Perhitungan nilai rata-rata gelombang sinus.
Gambar 6. Perhitungan nilai rata-rata gelombang sinus.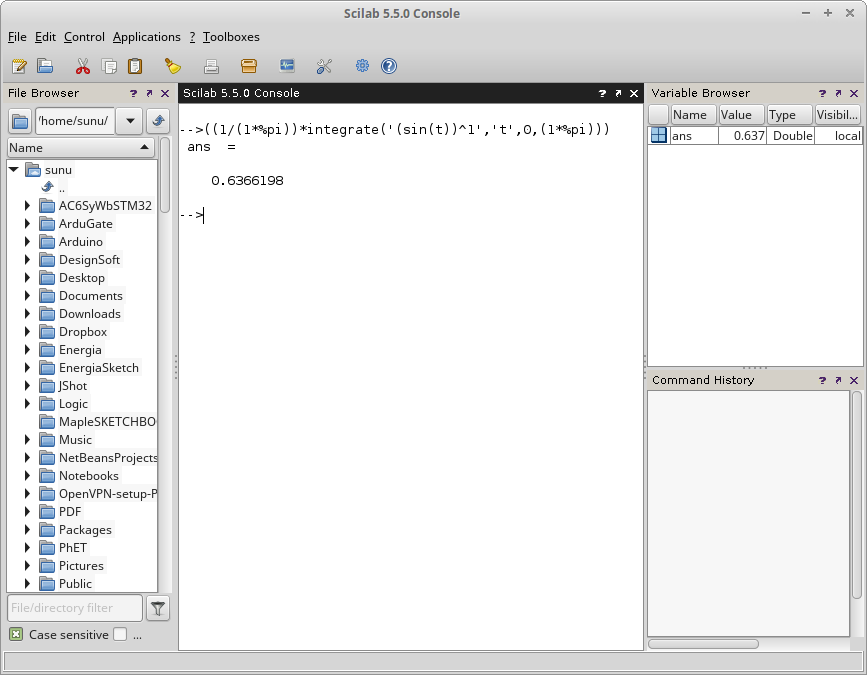 Gambar 7.
Gambar 7.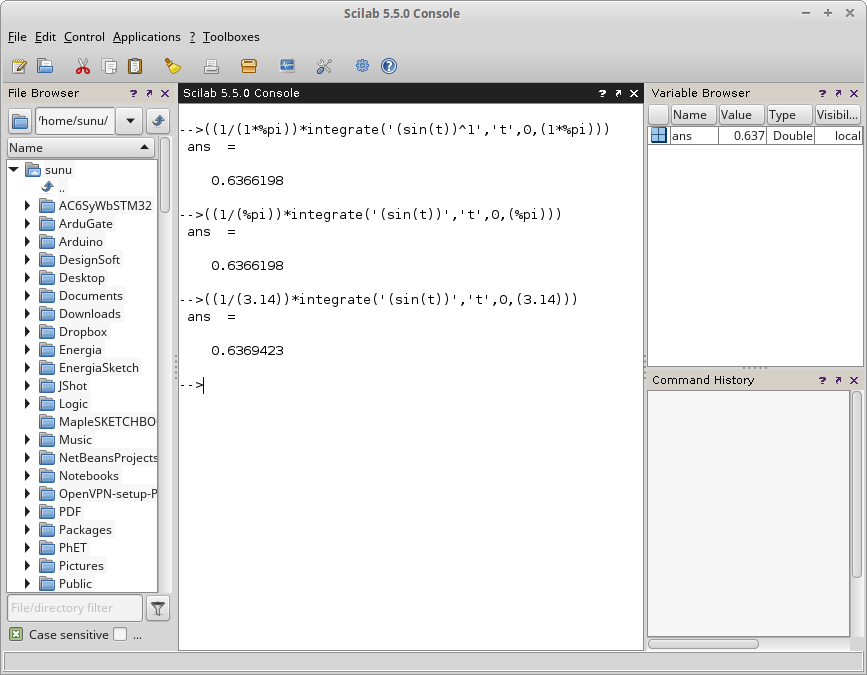 Gambar 8.
Gambar 8.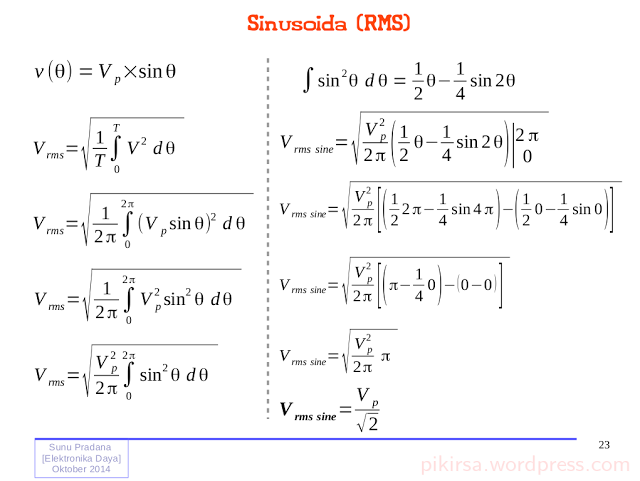 Gambar 9.
Gambar 9.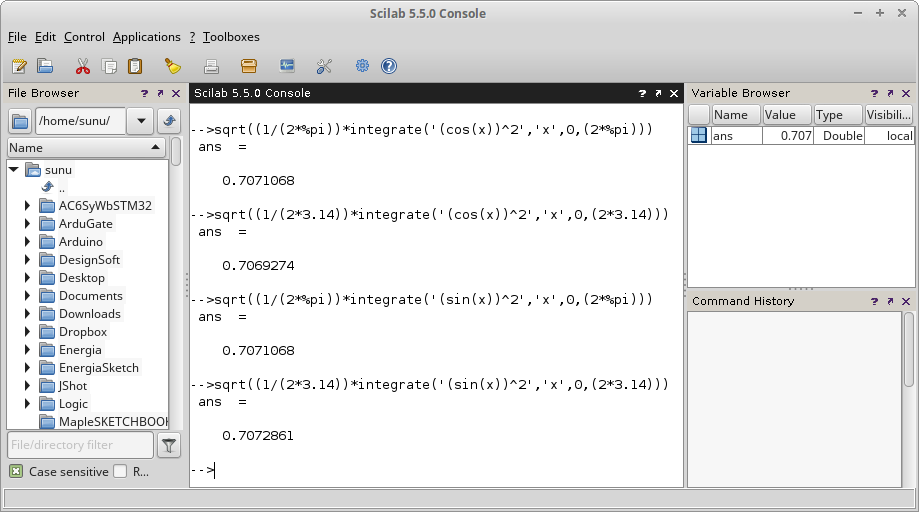 Gambar 11.
Gambar 11.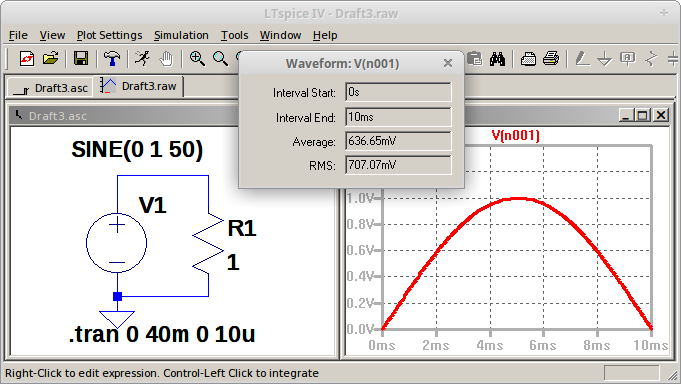 Gambar 12.
Gambar 12.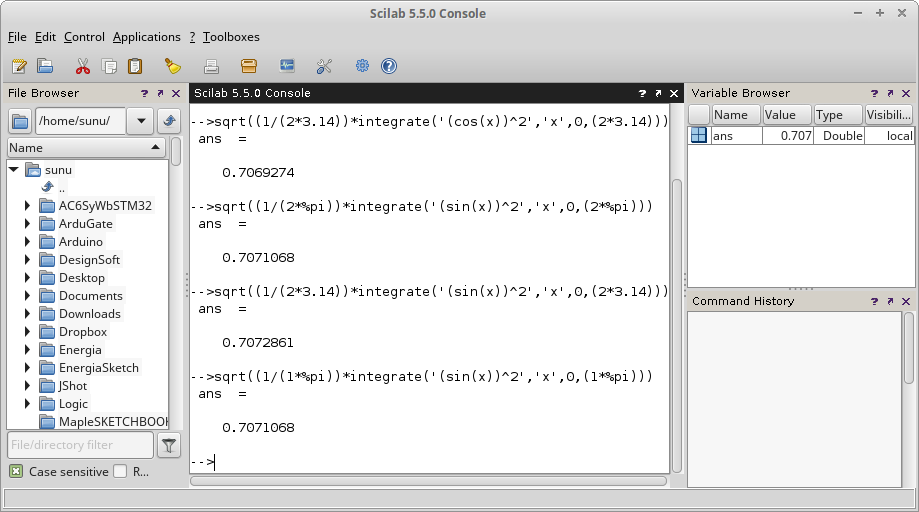 Gambar 13.
Gambar 13.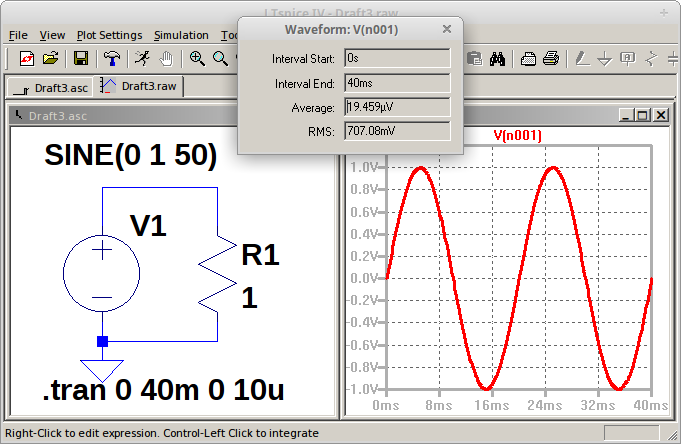 Gambar 14.
Gambar 14.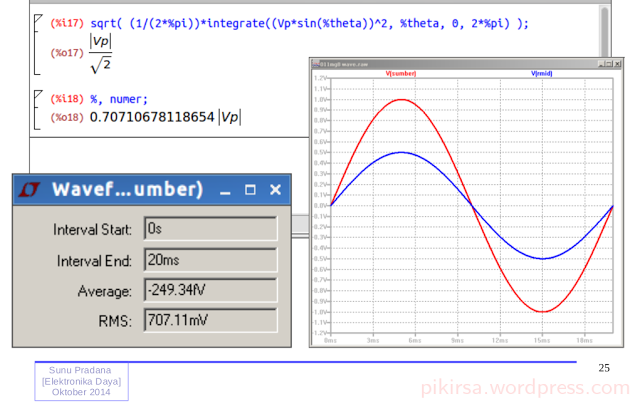 Gambar 15.
Gambar 15.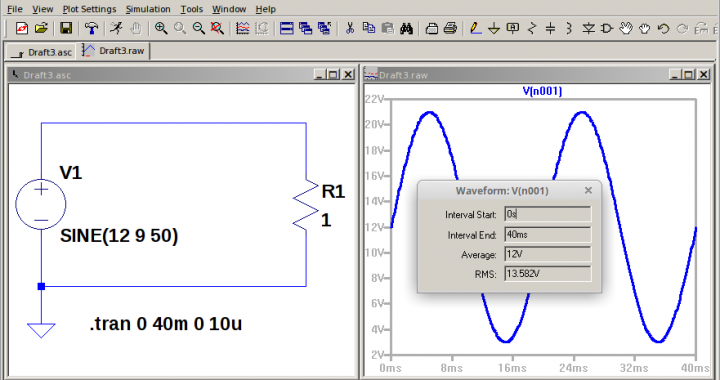
 Gambar 1.
Gambar 1.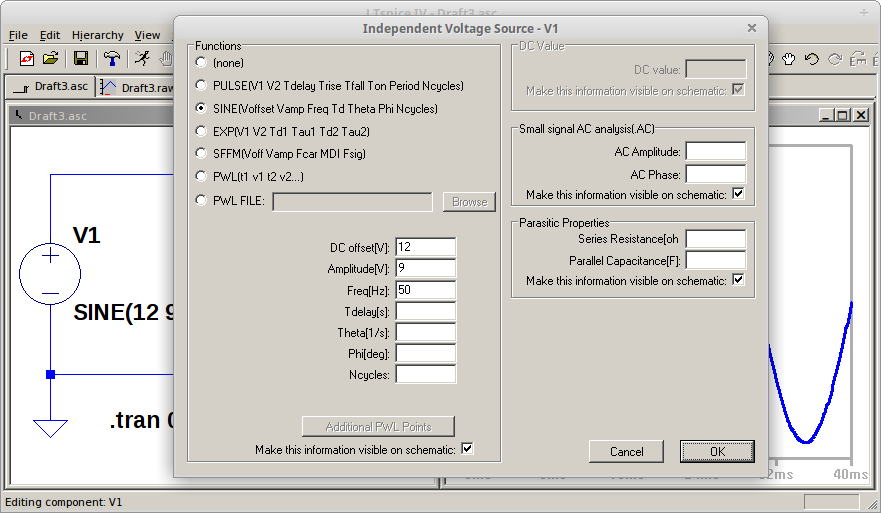 Gambar 2.
Gambar 2.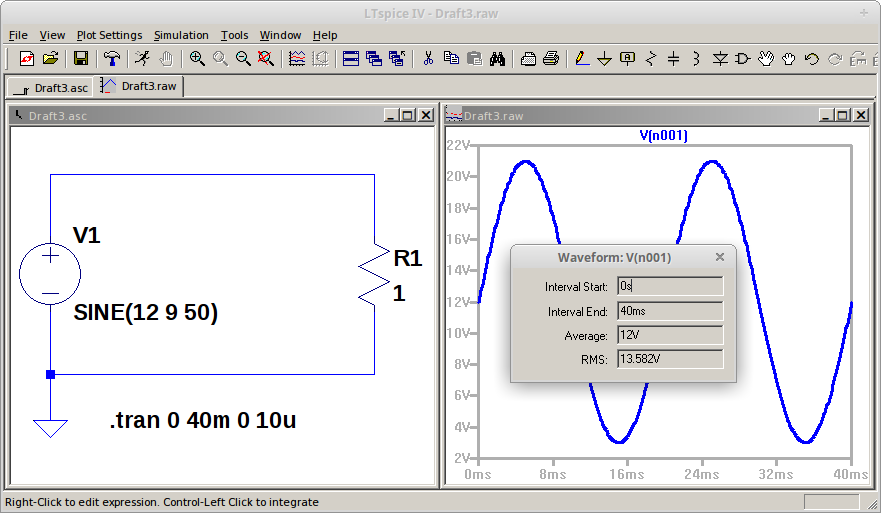 Gambar 3.
Gambar 3.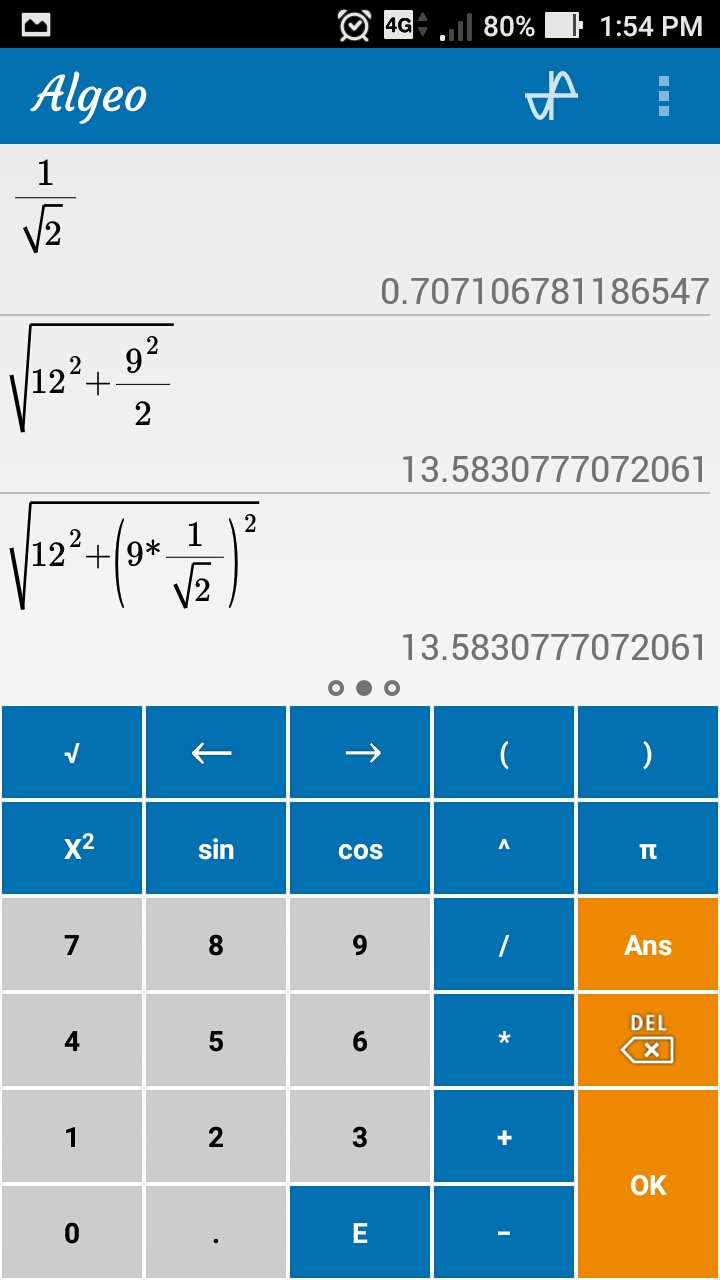
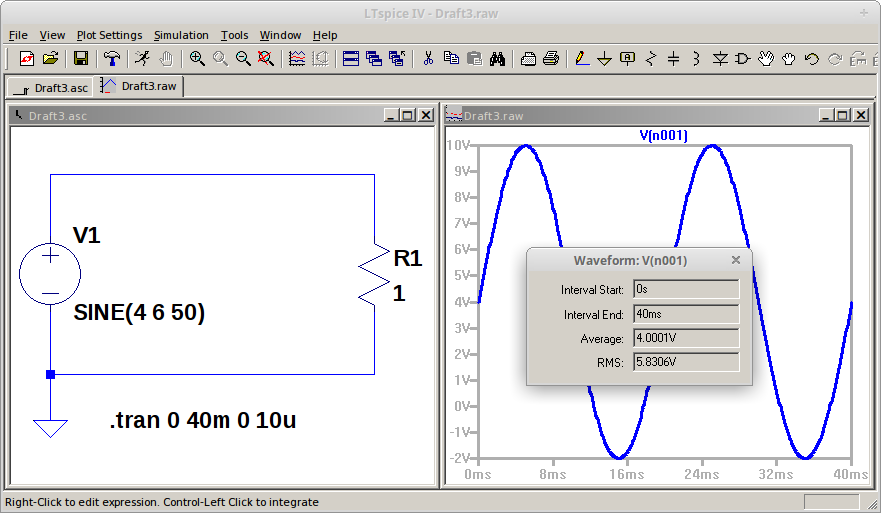 Gambar 5. Simulasi gelombang sinus dengan offset, puncak nilai positif dan negatif.
Gambar 5. Simulasi gelombang sinus dengan offset, puncak nilai positif dan negatif.





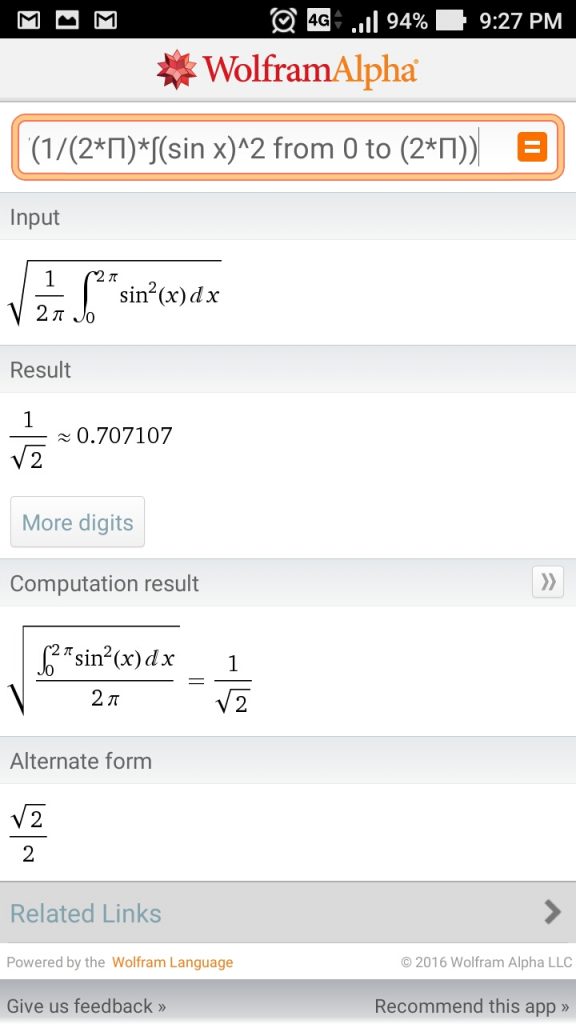
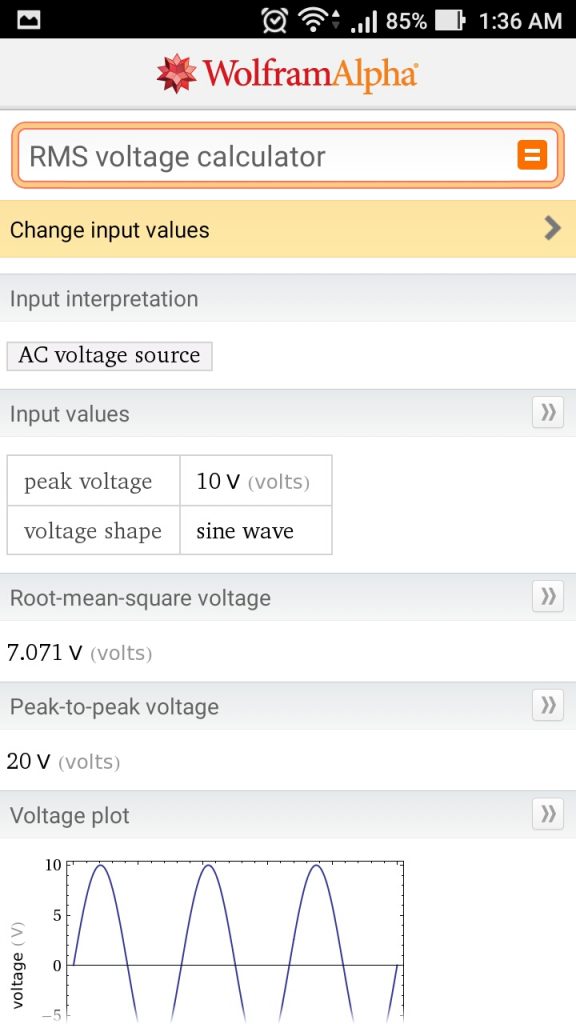
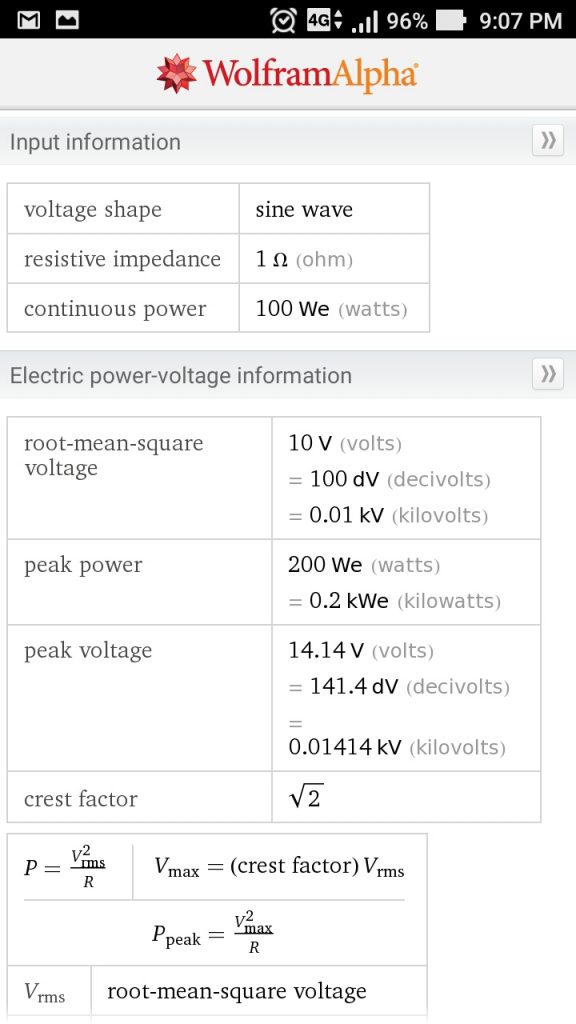

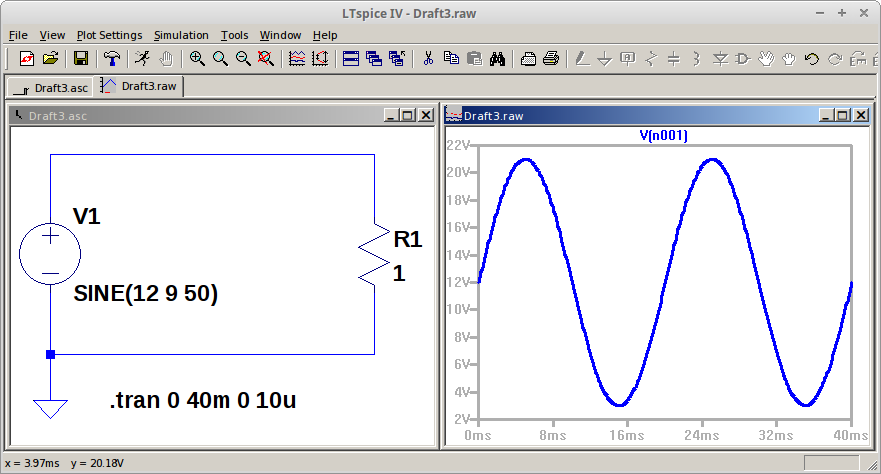
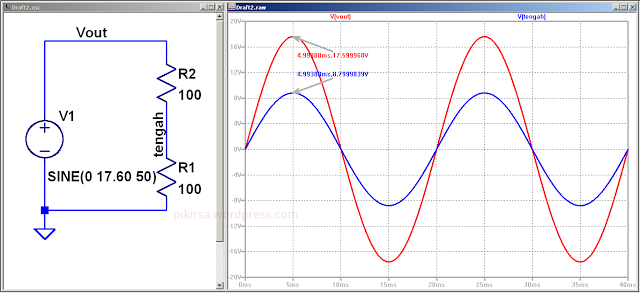 Gambar 1. Konfigurasi rangkaian percobaan
Gambar 1. Konfigurasi rangkaian percobaan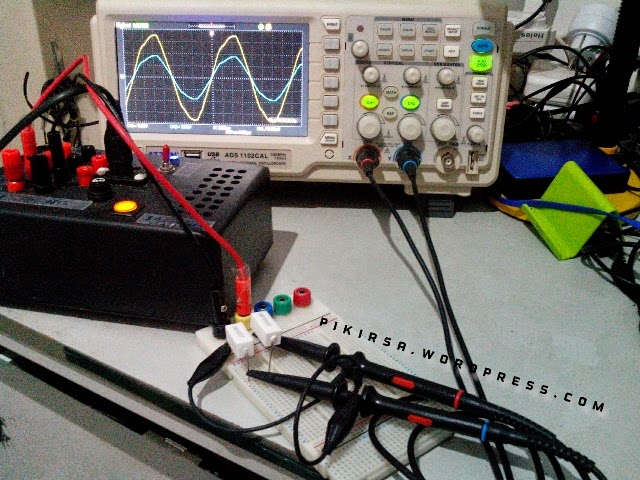 Gambar 2. Set-up uji dengan komponen.
Gambar 2. Set-up uji dengan komponen.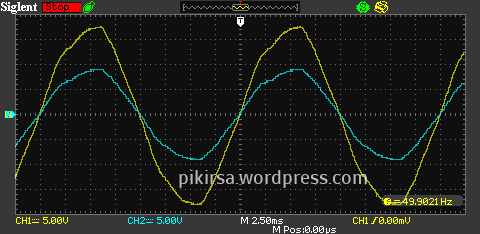 Gambar 3. Bentuk gelombang sinus pada kedua kanal menunjukkan bentuk gelombang sinus yang tidak ideal.
Gambar 3. Bentuk gelombang sinus pada kedua kanal menunjukkan bentuk gelombang sinus yang tidak ideal.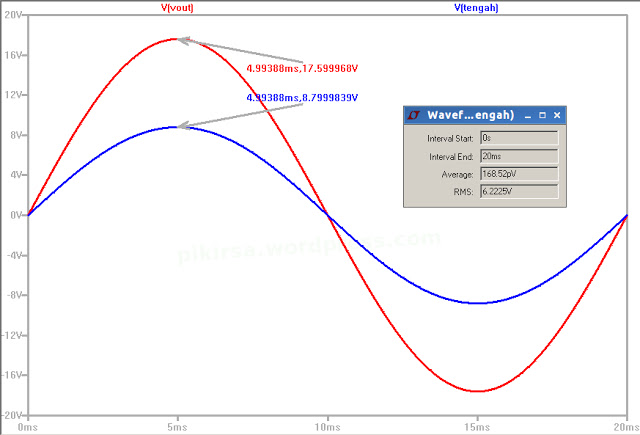 Gambar 4. Hasil simulasi rangkaian pada LTspice.
Gambar 4. Hasil simulasi rangkaian pada LTspice.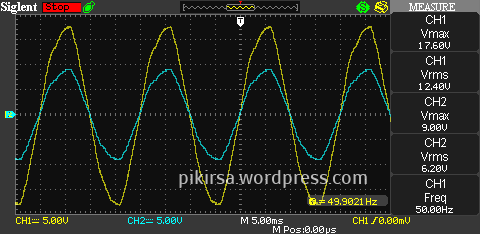 Gambar 5. Tampilan DSO dengan parameter utama gelombang di CH1 dan CH2.
Gambar 5. Tampilan DSO dengan parameter utama gelombang di CH1 dan CH2.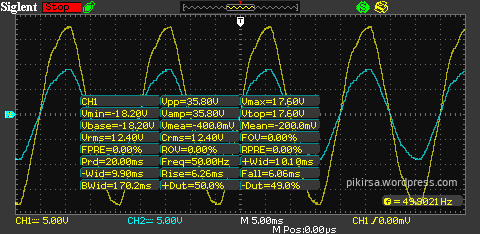 Gambar 6. Hasil pengukuran pada kanal satu (CH1) DSO pada tegangan terminal (node Vout).
Gambar 6. Hasil pengukuran pada kanal satu (CH1) DSO pada tegangan terminal (node Vout).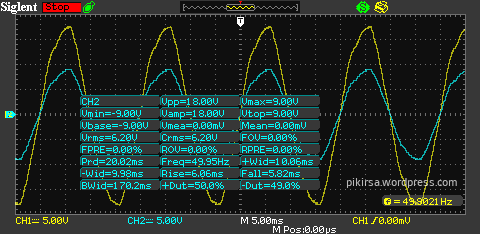 Gambar 7. Hasil pengukuran pada kanal dua (CH2) DSO pada tegangan node tengah.
Gambar 7. Hasil pengukuran pada kanal dua (CH2) DSO pada tegangan node tengah.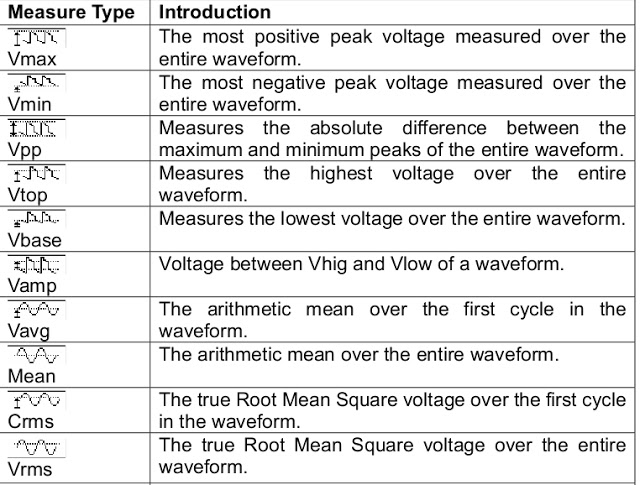 Gambar 8. Panduan istilah untuk memahami parameter hasil pengukuran DSO.
Gambar 8. Panduan istilah untuk memahami parameter hasil pengukuran DSO.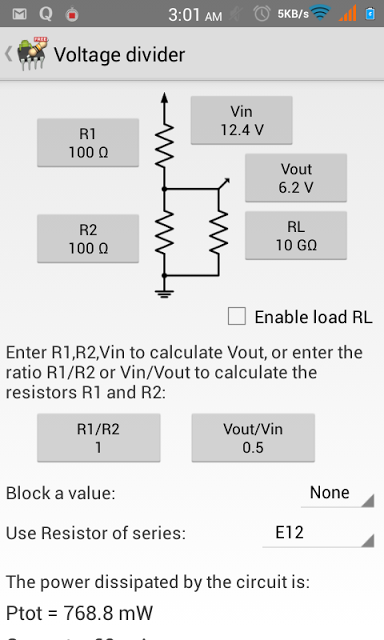 Gambar 9. Contoh pemanfaatan aplikasi Android untuk penghitungan pembagi tegangan.
Gambar 9. Contoh pemanfaatan aplikasi Android untuk penghitungan pembagi tegangan.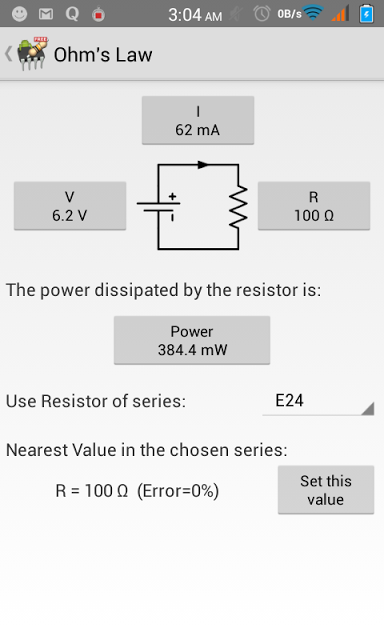 Gambar 10. Contoh penggunaan aplikasi untuk melihat hubungan berdasar hukum Ohm.
Gambar 10. Contoh penggunaan aplikasi untuk melihat hubungan berdasar hukum Ohm.