Motivasi
Pada artikel sebelumnya, telah dikumpulkan alur belajar tentang frekuensi, periode, duty cycle, dan PWM. Di artikel itu diharapkan sudah dapat terselesaikan permasalahan tentang pengukuran dan pengaturan waktu pada sinyal PWM.
Di instrumen oscilloscope hasil pengukuran rentang waktu yang berlalu ditampilkan pada sumbu horizontal. Pengaturan tampilan dilakukan dengan manipulasi pada knob time/div.
Langkah berikutnya adalah menentukan besar nilai sinyal. Bisa berupa nilai arus atau yang lebih sering adalah nilai tegangan. Di oscilloscope besar sinyal diukur pada sumbu vertikal. Pengaturan tampilan dilakukan dengan memanipulasi knob volt/div.
Dapatkah anda menghitung dan memahami nilai pengukuran dari simulasi pada Tina-TI di Gambar 1?
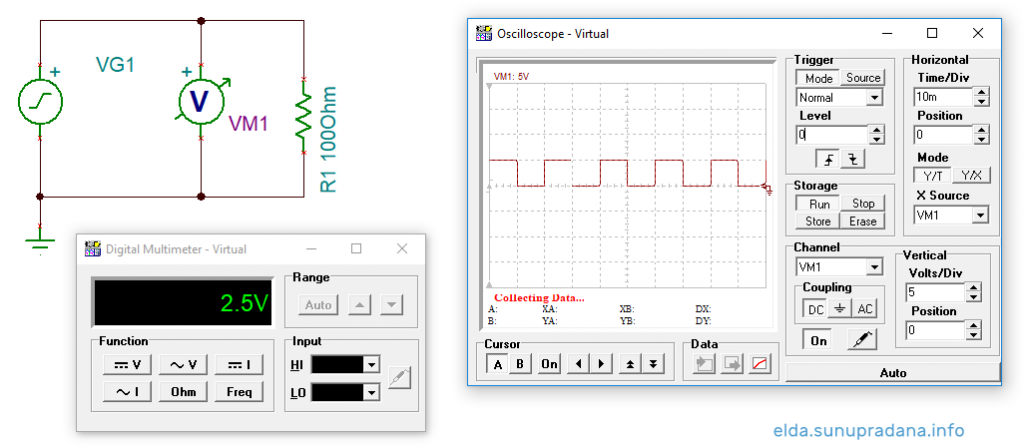
Rectangular, Square, Pulse train
Pengukuran besar sinyal tidak hanya memerlukan pengetahuan tentang besar nilai (absolut), tetapi juga memerlukan pengetahuan tentang bentuk gelombang dan polaritas.
Ada beberapa istilah yang bisa menimbulkan kebingungan, misalnya:
Rectangular wave, square wave, unidirectional waveforms, bidirectional waveforms, alernating waveforms, pulse, pulse train.
Penyebutan nama gelombang biasanya juga berdasar pada tipenya secara matematis.
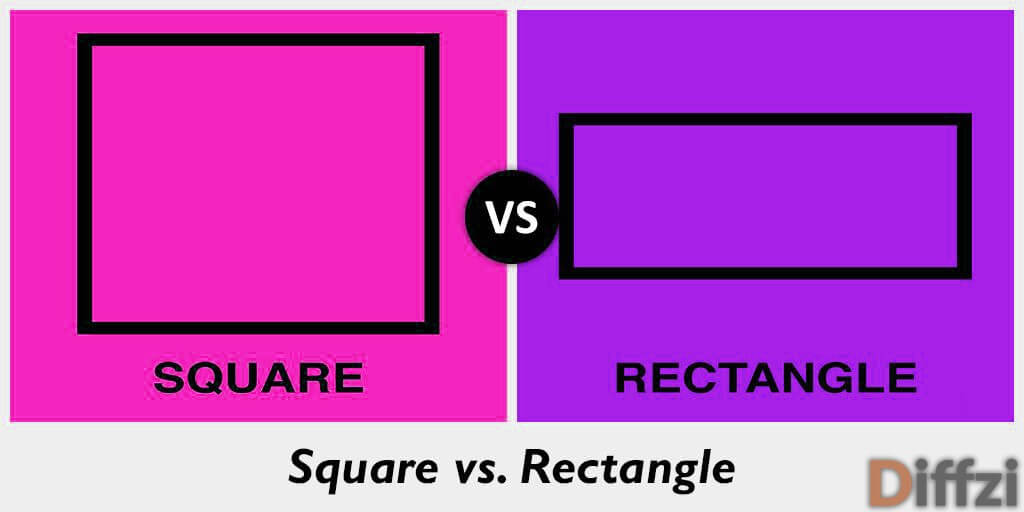
Gambar di atas ini mungkin akan dapat cepat mengingatkan kita akan perbedaan keduanya.
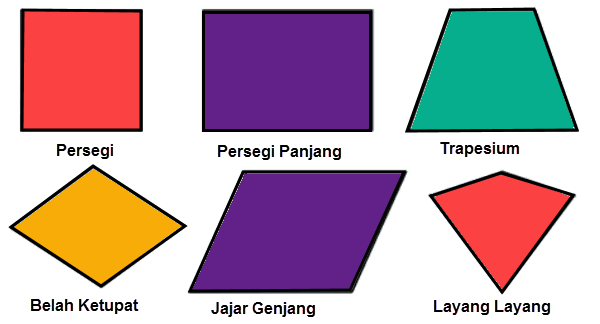
Kata rectangle dapat ditermahkan menjadi segi empat atau (yang lebih tepat) persegi panjang. Berikut ini ilustrasi yang diambil dari Wikipedia:
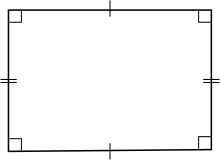
Sedangkan segi empat yang sama sisi disebut sebagai square. Biasa diterjemahkan sebagai persegi atau (yang lebih umum) bujur sangkar. Berikut adalah gambar dari Urban Dictionary:
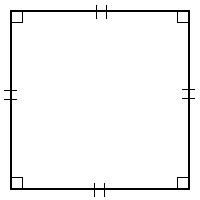
Sudahkah menjadi jelas perbedaan antara square dengan rectangle? Jika belum, lihatlah gambar yang diperoleh dari Quora berikut ini:
Dalam bahasa Indonesia, kadang-kadang beberapa penyebutan berbeda mengacu pada geometri yang sama.
Silakan baca artikel menarik dengan penjelasan rinci dari mikirbae yang salah satu gambarnya saya kutip sebagai berikut:
Juga penjelasan dan contoh soal dari situs “ukuran dan satuan“:
Istilah atau kata kotak sendiri memiliki konsekuensi adanya volume. Tetapi kata ini sering dipergunakan untuk menggambarkan sesuatu yang memiliki bentuk dua dimensi seperti persegi/bujur sangkar dan persegi panjang. Maka sering ditemui istilah ‘gelombang kotak’.
Setelah menyegarkan kembali ingatan tentang persamaan dan perbedaan antara square (persegi atau bujur sangkar) dengan rectangle (segi empat atau persegi panjang), kita bisa melanjutkan ke penerapannya pada penamaan gelombang.
Penamaan ‘gelombang kotak’ dapat menimbulkan kerancuan jika tidak diperhatikan dan dipilah dengan baik. Untuk itu setelah frekuensi dan periode dibahas di artikel sebelumnya, kali ini kita lanjutkan dulu pembahasan mengenai penamaan gelombang berdasarkan lebar pulsanya (pulse width) baru kemudian mempelajari mengenai polaritas sinyal.


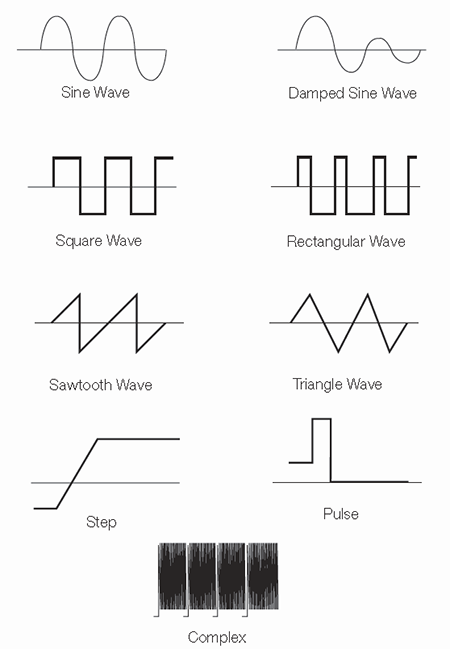
Gambar 2 yang diperoleh dari Wikipedia memperlihatkan perbandingan antara square wave dengan bentuk gelombang yang lain. Abaikan terlebih dahulu amplitudo dan polaritas gelombang. Perhatikan dulu lebar pulsanya (pulse width), perbandingan antara waktu ON (high) terhadap waktu OFF (low).
Gambar 3, yang juga diperoleh dari Wikipedia menunjukkan gelombang yang dinamakan sebagai rectangular wave atau pulse wave atau pulse train. Bisa dilihat bahwa lebar pulsa tidak lagi 50 %, meskipun bentuknya sama-sama menyerupai ‘kotak’.
Dikatakan juga bahwa square wave (gelombang persegi atau bujur sangkar) merupakan ‘kasus khusus’ dari rectangular wave. Yaitu suatu rectangular wave yang memiliki duty cycle sebesar 50 %.
Setelah memahami persamaan dan perbedaan antara square wave dengan rectangular wave berdasarkan lebar pulsa (pulse width) arau duty cycle, berikutnya kita akan melihatnya dari sisi polaritas sinyal.
Suatu sinyal (signal) dikatakan memiliki polaritas yang berbalik (alternate) jika amplitudonya berubah/berpindah dari positif ke negatif, atau sebaliknya. Bisa juga disebut sebagai bidirectional waveforms atau alernating waveforms.
Sinyal yang tidak pernah mengalami perubahan polaritas disebut sebagai unidirectional waveforms. Baik square wave maupun rectangular wave (selain square wave) dapat merupakan sinyal yang unidirectional maupun bidirectional/alternating/bipolar.
Gambar 4 diperoleh dari situs produsen instrumen elektronik Tektronix. Pada gambar itu baik square wave maupun rectangular wave merupakan alternating wave/bidirectional wave/bipolar. Berbeda dengan Gambar 3 yang menunjukkan rectangular wave yang unipolar.
Pemahaman ini penting karena kadang-kadang ditemui keterangan/gambar yang hanya menyampaikan kombinasi yang tidak lengkap. Misalnya pada Gambar 5 berikut ini yang diperoleh dari situs yang sangat bagus dalam membahas ilmu elektrikal milik James Irvine. Pada tabel di Gambar 5 di bawah ini square wave yang ditampilkan merupkan gelombang yang alternating wave/bipolar wave/bidirectional wave. Sedangkan rectangular wave yang ditampilkan adalah unidirectional wave. Yaitu gelombang yang nilainya positif saat high, dan akan bernilai 0 saat low.
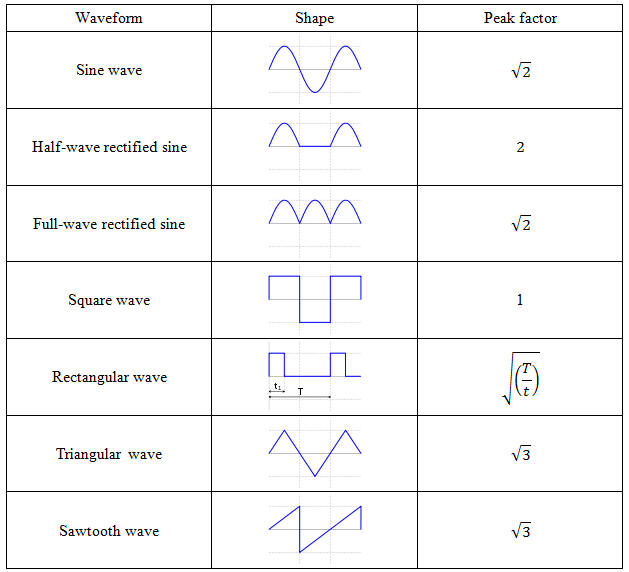
Unidirection Rectangular Wave
Untuk memudahkan pembahasan, kita mengikuti filosofi bahwa sebaiknya kita belajar dengan sesuatu yang sederhana terlebih dahulu. Setelah bentuk yang sederhana dipahami barulah secara bertahap kita dapat menambah kompleksitas bahan belajar. Untuk itu, dalam belajar melakukan perhitungan amplitudo gelombang kotak (square wave/rectangular wave), kita sebaiknya mulai dari tipe unidirectional wave. Sinyal yang akan dihitung hanya berada dalam satu polaritas saja yaitu wilayah positif. Pada keadaan terendahnya sinyal ini akan bernilai 0 (nol) volt atau 0 (nol) ampere.
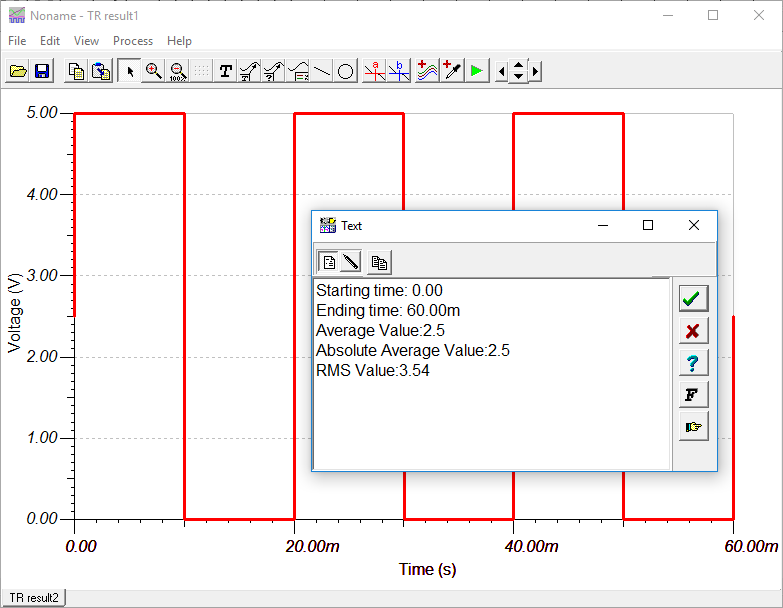
Dapatkah anda menghitung nilai average (rata-rata) dan rms pada Gambar 6, yang merupakan hasil simulasi dengan Tina-TI, di atas?
Gelombang pada Gambar 6 adalah square wave, yaitu sinyal PWM rectangular wave yang memilki duty cycle sebesar 50 %. Lebar pulsa, pulse width atau positive pulse width sebesar 10 ms. Periode untuk satu siklus penuh adalah 20 ms. Tegangan maksimum pada saat ON (high) adalah 5 V, sedangkan tegangan minimum saat OFF (low) adalah sebesar 0 V.
Persamaan berikut dipakai untuk mencari nilai rata-rata (average):
Untuk sinyal pada Gambar 6, perhitungan akan seperti ini:
Untuk mencari nilai rms (root-mean-square) dari gelombang kotak persegi (square wave) dapat dipakai persamaan berikut:
Untuk sinyal pada Gambar 6, akan didapat hasil:
Kedua perhitungan itu sebenarnya sama, tetapi berbeda cara dalam menyatakan pemisahan nilai desimal. Yang satu menggunakan ‘koma’ dengan tanda koma (,) sedang yang lain menggunakan tanda titik (.) untuk ‘koma’ (pemisah nilai desimal).

Pada Gambar 7, dapat dilihat gelombang kotak yang merupakan rectangular wave. Yaitu pulse train dari PWM yang duty cycle-nya tidak bernilai 50 %. Nilai pulse width (pulse active time) sebesar 5 ms, sedangkan nilai negative pulse width sebesar 15 ms, sehingga nilai periode sebesar 20 ms.
Pada bentuk sinyal seperti ini, nilai rata-rata (misalnya tegangan rata-rata) dapat dihitung dengan persamaan berikut:
Untuk Gambar 7, hasil perhitungan akan seperti ini:
Anda mungkin memperhatikan bahwa sekalipun hasilnya berbeda, tetapi persamaan untuk mencari nilai rata-rata pada Gambar 7 sama dengan persamaan rata-rata pada Gambar 6. Bedanya pada square wave nilai positive pulse width selalu setengah dari besar nilai periode.
Untuk mencari nilai rms pada rectangular wave seperti pada Gambar 7 dipergunakan persamaan berikut:
Persamaan ini juga dapat dipergunakan pada unidirectionial square wave karena gelombang itu merupakan kasus khusus dari unidirectional rectangular wave.
Hasil perhitungan untuk Gambar 7 akan seperti ini:
Bidirection Rectangular Wave
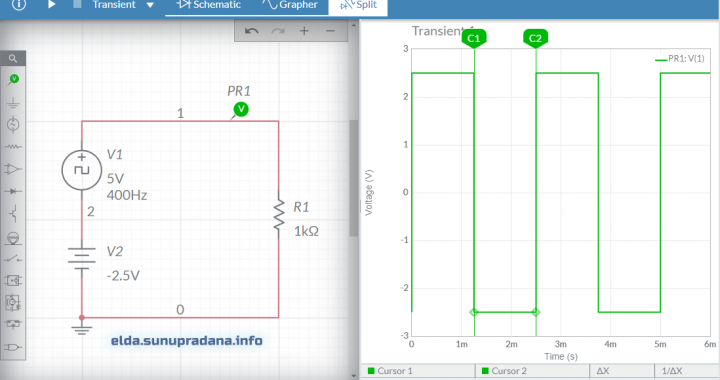
Pada percobaan dasar di laboratorium elektronika daya, umumnya yang dipergunakan adalah unidirectionial wave. Tetapi kadang-kadang kita akan menemui gelombang yang bipolar, memiliki nilai positif dan negatif. Seperti simulasi dengan Multisim Live pada Gambar 8 berikut ini.
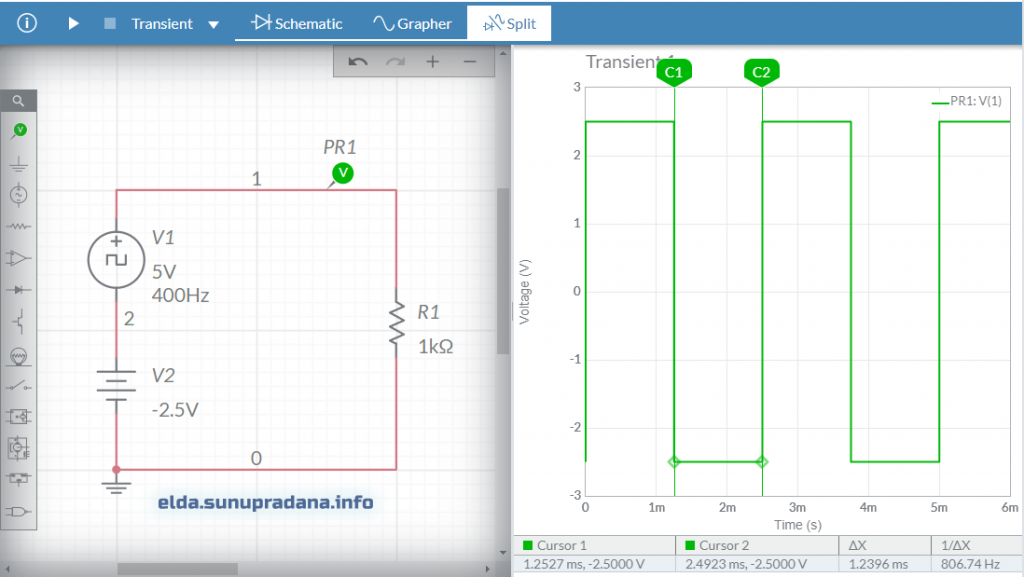
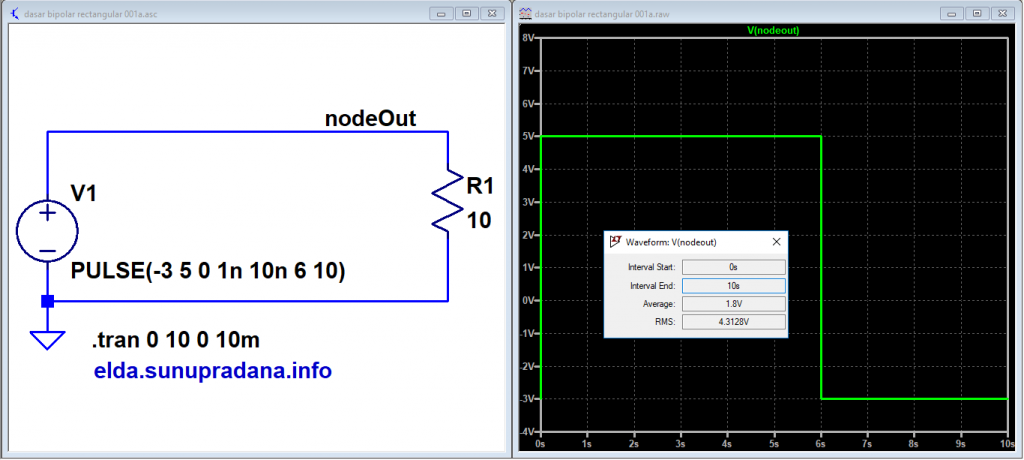

Untuk mempermudah belajar kita akan mencari contoh yang mudah untuk dipahami. Saya menemukan contoh yang bagus untuk dijadikan bahan belajar untuk menentukan nilai rata-rata bipolar/bidirectional rectangular wave. Gambar 9 adalah visualisasi dengan simulasi LTspice dari contoh perhitungan yang saya capture dan tampilkan pada Gambar 10. Kuncinya adalah perthitungan integral (jumlah) dari keseluruhan nilai amplitudo sinyal (misalnya tegangan) untuk seluruh rentang periode dibagi dengan periode. Pada kedua gambar dapat dilihat bahwa nilai rata-rata sama dengan 1,8 V.
Untuk mencari nilai rms pada Gambar 9 di atas (klik Gambar 9 untuk memperbesar tampilan), maka diperlukan persamaan sebagai berikut:
Pada contoh Gambar 9 hasil perhitungannya akan sama dengan hasil simulasi, yaitu:
Bagaimana dengan rectangular wave yang memiliki postur simetris seperti pada Gambar 8 di atas? Kita dapat melakukan simulasi kembali dengan LTspice seperti pada Gambar 11.
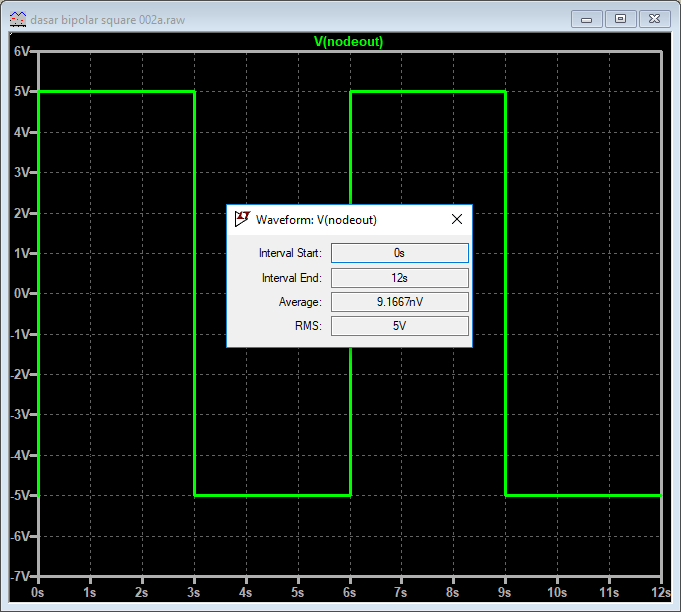
Hasil simulasi LTspice pada Gambar 11 dapat dibandingkan dengan perhitungan manual. Perhitungan untuk nilai rata-rata dapat menggunakan persamaan yang sama seperti pada Gambar 10. Baik hasil perhitungan maupun penalaran sederhana akan menghasilkan nilai yang sama, yaitu 0 (nol). Luas wilayah positif sama persis dengan luas wilayah negatif, karena itu nilai rata-ratanya sama dengan nol.
Adapun hasil pada Gambar 11 yaitu 9,1667 nV merupakan ketidakidealan yang dapat diabaikan dan diartikan sama dengan nol untuk gelombang ideal. Pengukuran pada sistem fisik juga akan memberikan nilai yang hampir selalu tidak ideal. Baik karena bentuk sinyal/gelombangnya ataupun karena akurasi & resolusi sistem alat ukurnya.
Pada Gambar 11 di atas pula bisa kita lihat nilai rms yaitu sebesar 5 V. Memang untuk bidirectional square wave/bipolar pulse waveform seperti itu, nilai rms selalu sama dengan nilai puncaknya.
Jika tertarik untuk lebih lanjut mempelajari tentang perhitungan rectangular wave/square wave baik yang unidirectional maupun yang alternating / bipolar / bidirectional, dapat membaca dua artikel berikut:
- How to derive the rms value of pulse and square waveforms
- RMS of A Square Pulse Train – John Dunn, Consultant, Ambertec, P.E., P.C.
TEXT:
- Square [Wikipedia]
- Square [Math is fun]
- Square [Britannica]
- Difference Between Square vs. Rectangle
- Rectangle [Wikipedia]
- Theorems about Quadrilaterals
- rectangle
- What is the difference between a square and a rectangle?
- Jenis dan Sifat Segiempat
- Berapa Jumlah Besaran Sudut dalam Suatu Bidang Segi Empat?
- Electropedia
- A Dictionary of Electronics and Electrical Engineering (5 ed.)
- KBBI Daring
- Frequency [Wikipedia]
- What is frequency?
- Frequency [earthguide]
- Wave Variables [Texas Gateway]
- Square pulse train [electropedia]
- Electrical Waveforms
- Square wave [Wikipedia]
- Pulse wave [Wikipedia]
- Square Wave
- Tutorial 2 – Waveforms
- How to derive the rms value of pulse and square waveforms
- RMS of A Square Pulse Train – John Dunn, Consultant, Ambertec, P.E., P.C.
- Waveform and Signal Analysis
- What is duty cycle?
- Pulse Width Modulation
- Duty cycle [Wikipedia]
- Laureate Duty Cycle & Pulse Width Modulation (PWM) Meter
- analogWrite()
- Secrets of Arduino PWM
- Arduino-PWM-Frequency
- What is a Pulse Width Modulation (PWM) Signal and What is it Used For?
- Pulse Width Modulation
- Pulse-width modulation [Wikipedia]
- Pulse Width Modulation
- PWM
- Pulse Width Modulation [Sparkfun]
- What is PWM (Pulse Width Modulation)?
- Basic – Pulse Width Modulation (Pwm)
- Introduction to Pulse Width Modulation
- PWM – Pulse Width Modulation Tutorial | CCP Module
- Pulse width modulation (PWM) components
- Pulse Width Modulation (PWM) [Comlab]
- Frequency-controlled induction motor drive systems

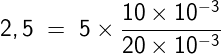
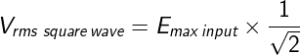
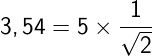
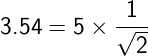


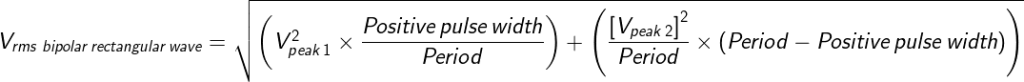

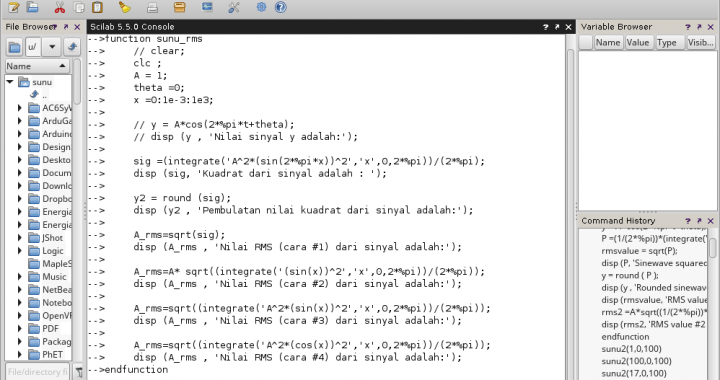
 Gambar 1.
Gambar 1.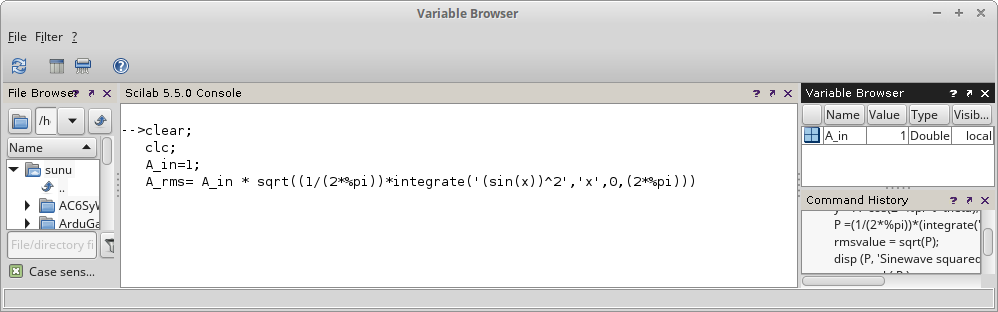 Gambar 2.
Gambar 2.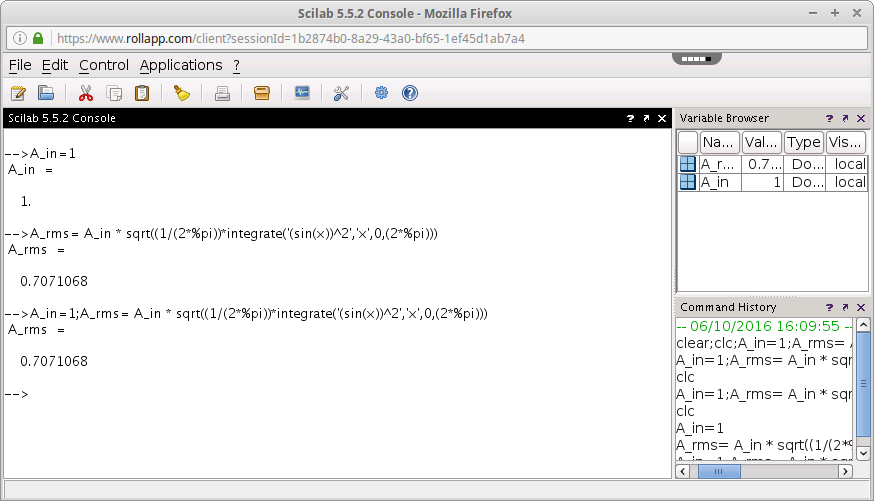 Gambar 3. Hasil perhitungan.
Gambar 3. Hasil perhitungan.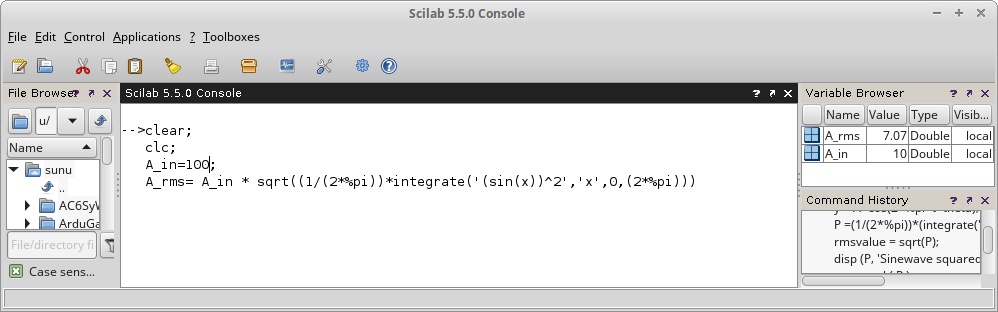 Gambar 4. Nilai A_in diganti menjadi 100.
Gambar 4. Nilai A_in diganti menjadi 100.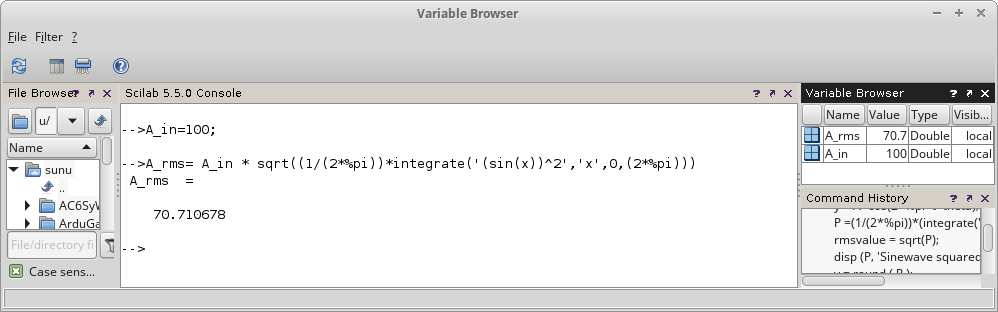 Gambar 5. Hasil perhitungan, nilai A_rms.
Gambar 5. Hasil perhitungan, nilai A_rms.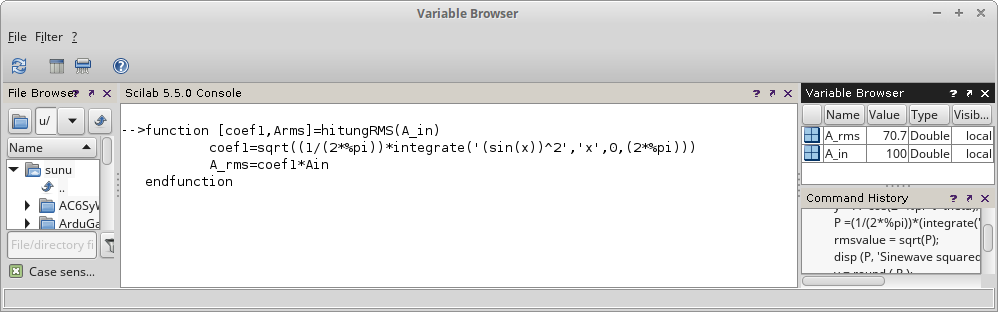 Gambar 6.
Gambar 6.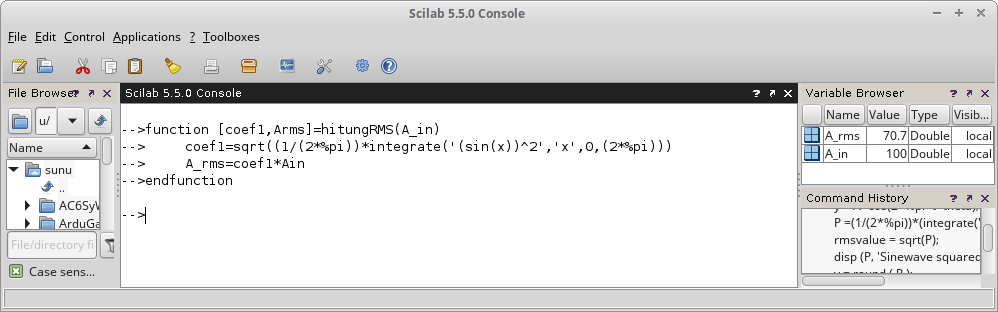 Gambar 7.
Gambar 7.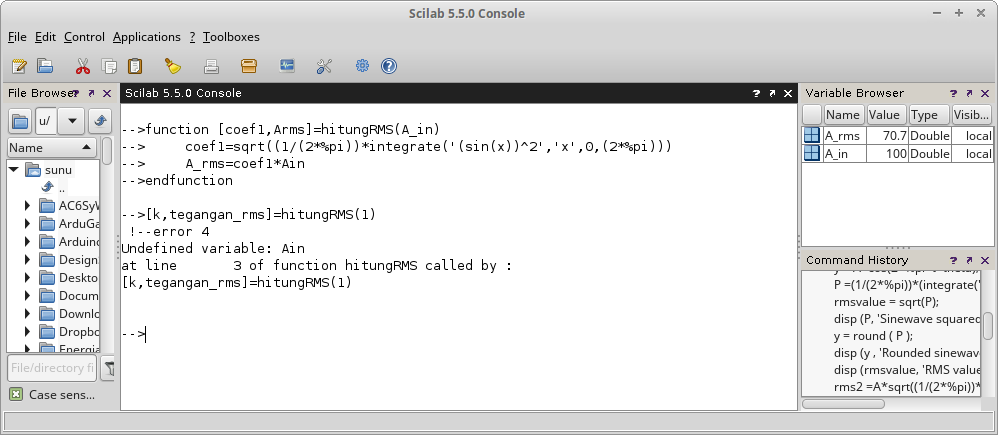 Gambar 8.
Gambar 8.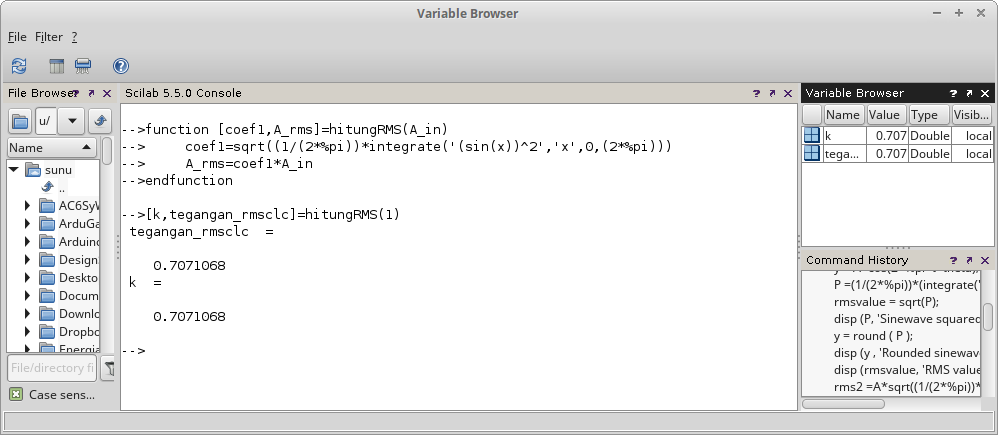 Gambar 9. Penampilan hasil perhitungan dalam
Gambar 9. Penampilan hasil perhitungan dalam 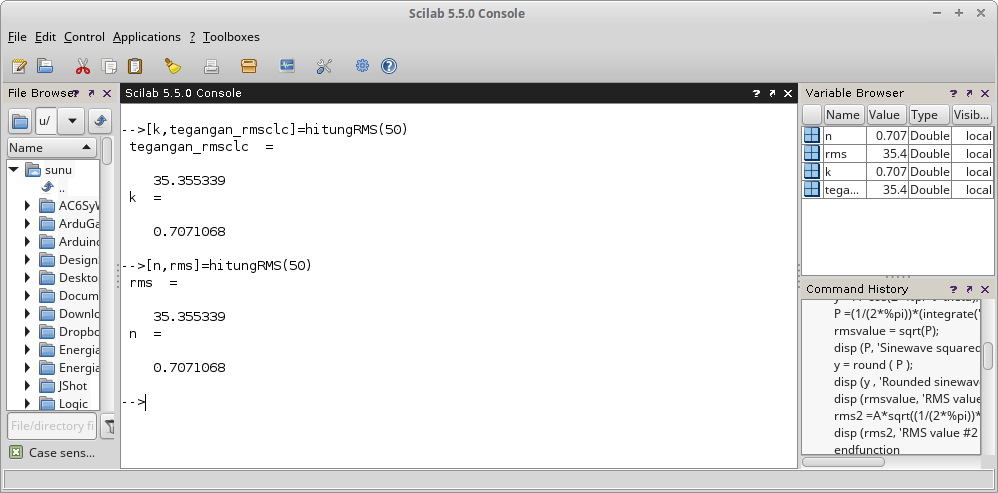 Gambar 10. Penamaan
Gambar 10. Penamaan 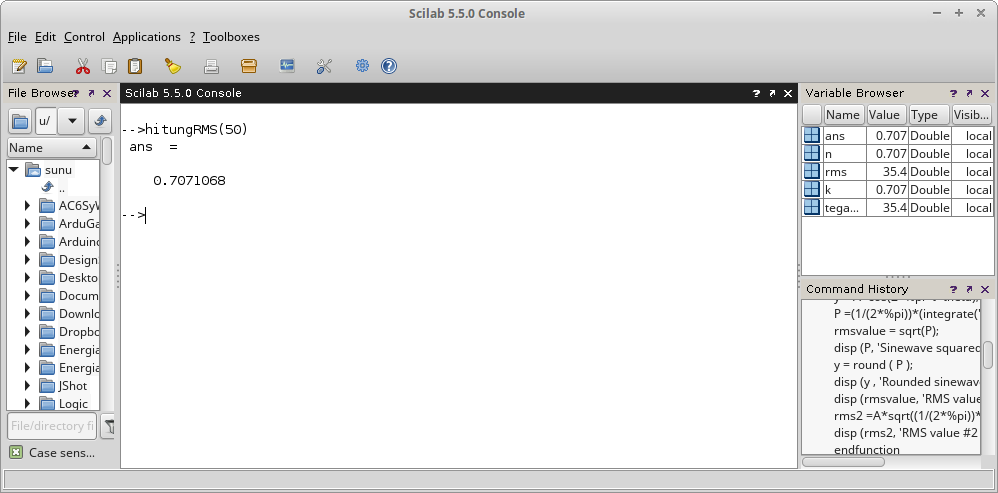 Gambar 11. Pemanggilan fungsi tanpa menyediakan
Gambar 11. Pemanggilan fungsi tanpa menyediakan 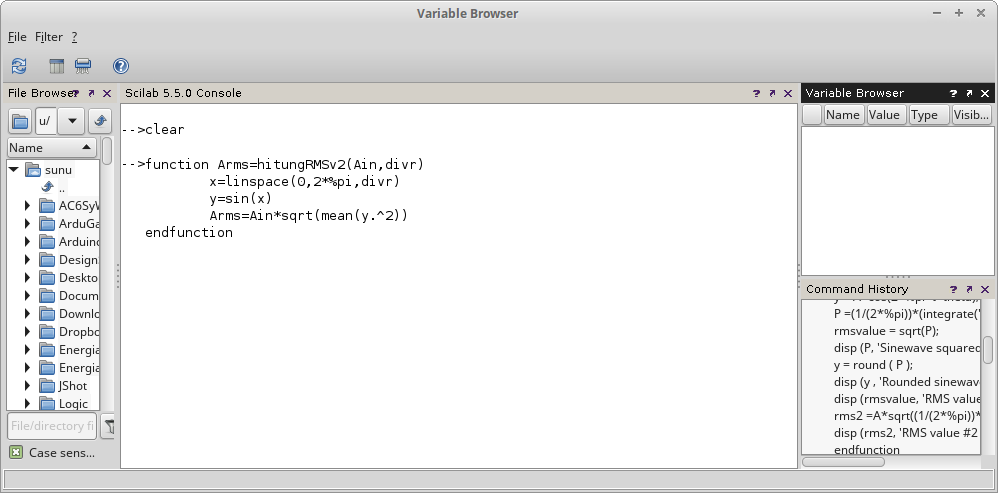 Gambar 12.
Gambar 12.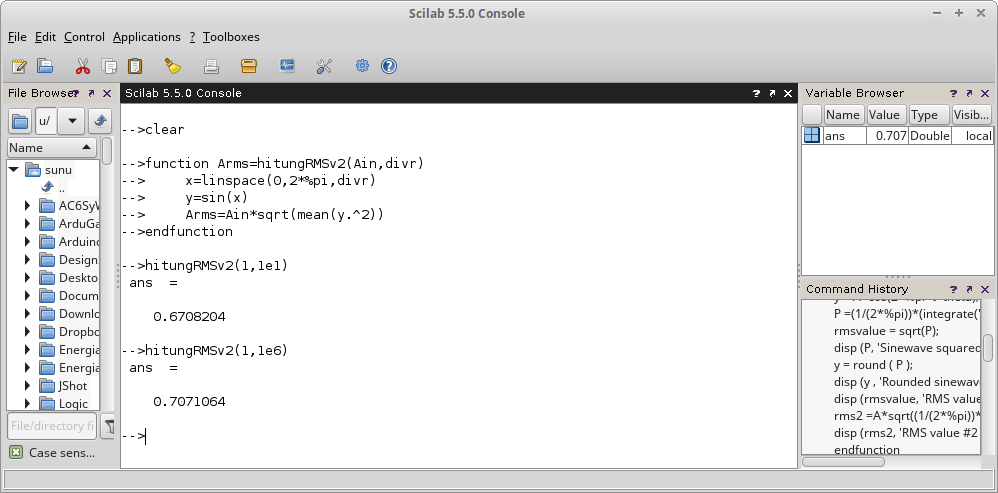 Gambar 13.
Gambar 13.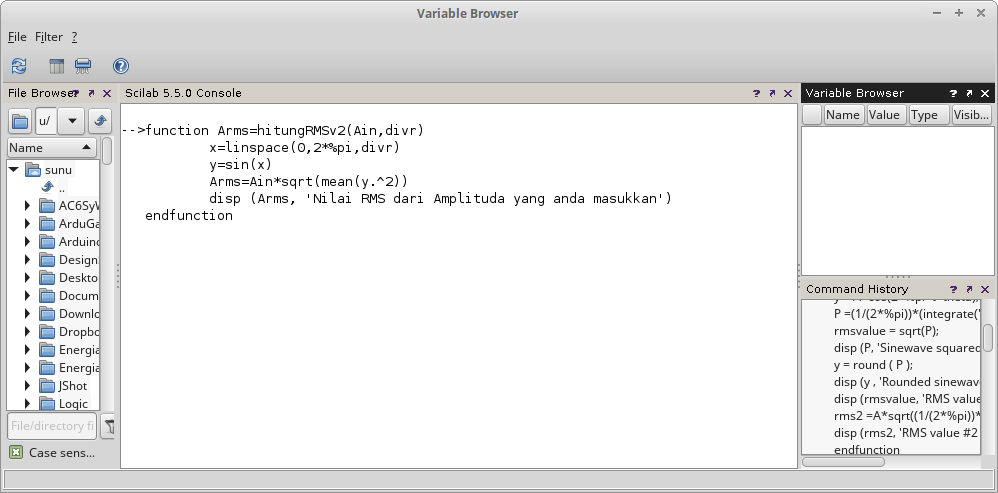 Gambar 14.
Gambar 14.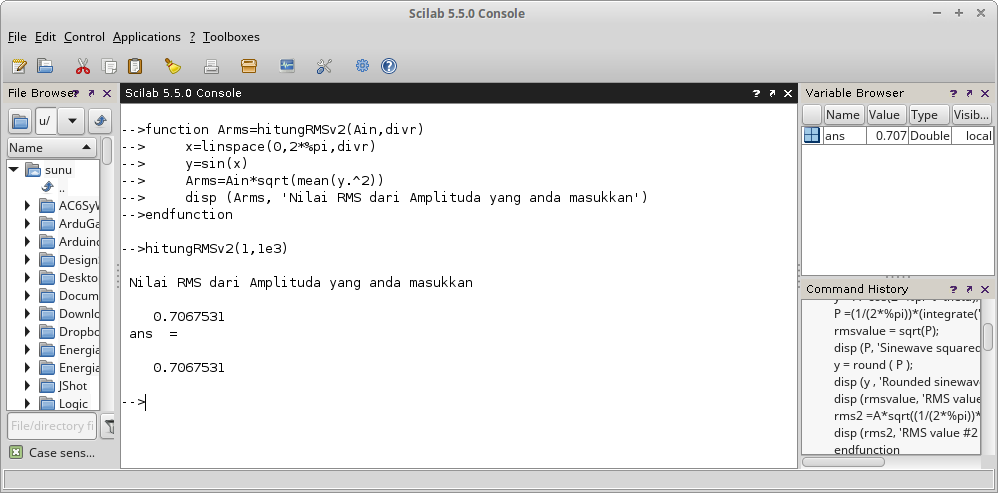 Gambar 15.
Gambar 15.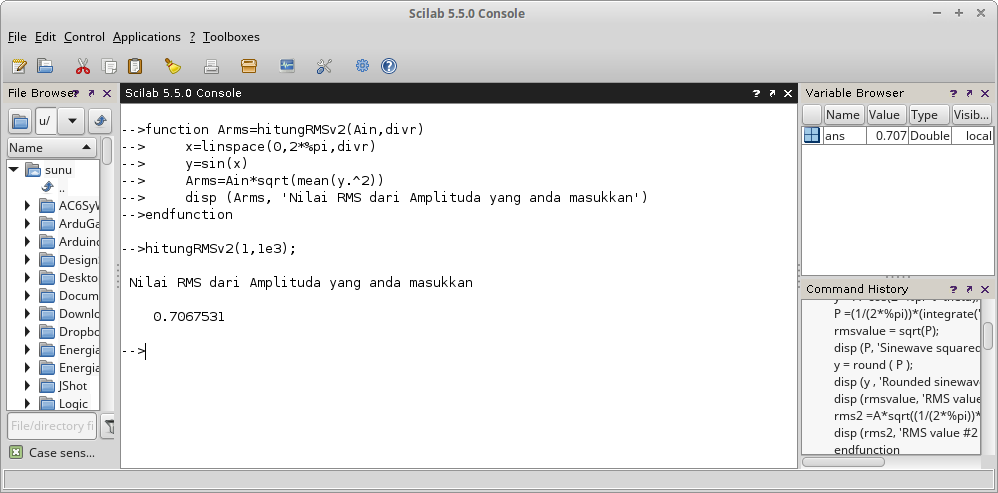 Gambar 16.
Gambar 16.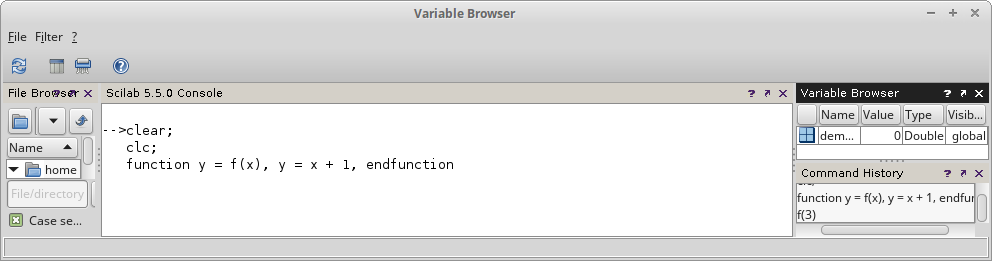 Gambar 17.
Gambar 17.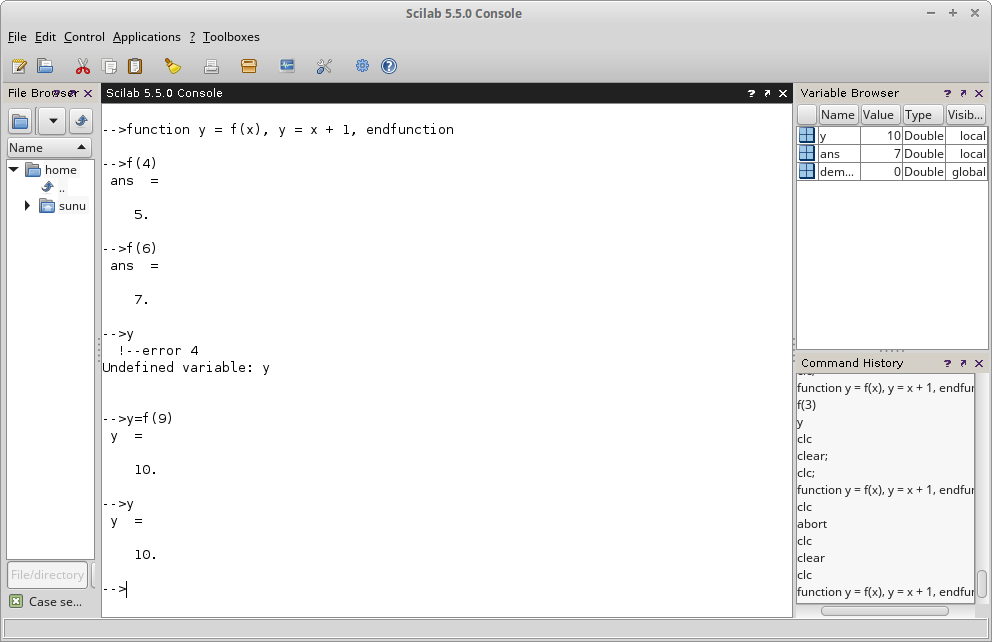 Gambar 18.
Gambar 18.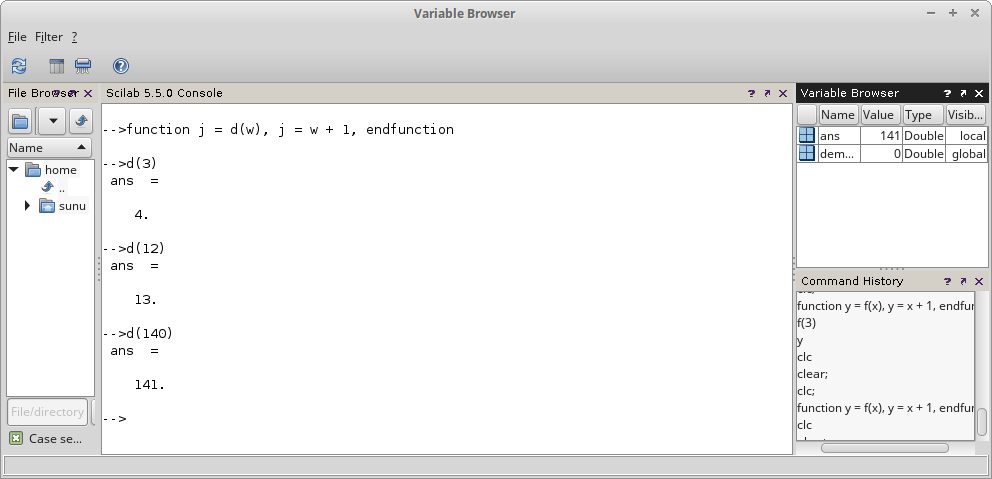 Gambar 19.
Gambar 19.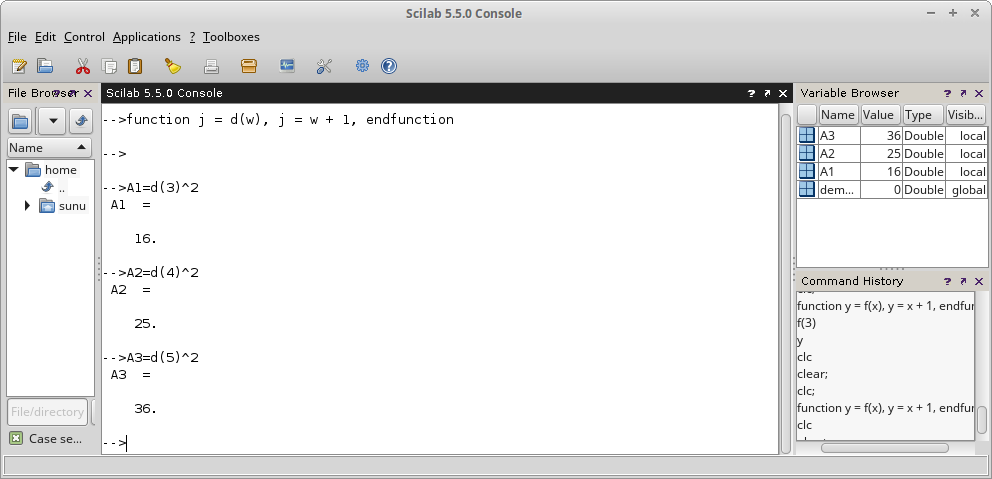 Gambar 20.
Gambar 20.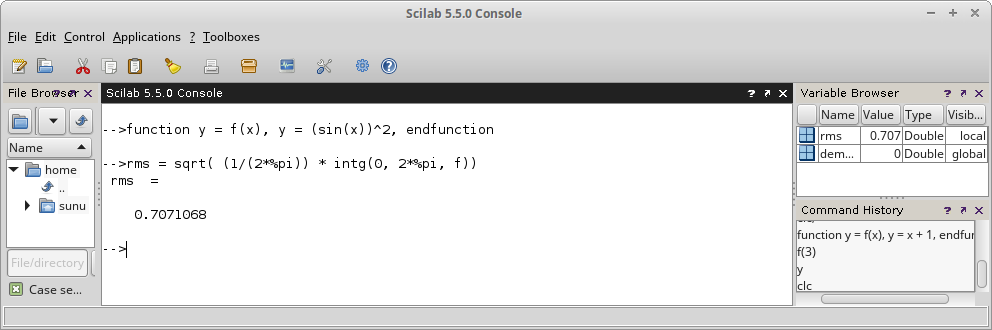 Gambar 21.
Gambar 21.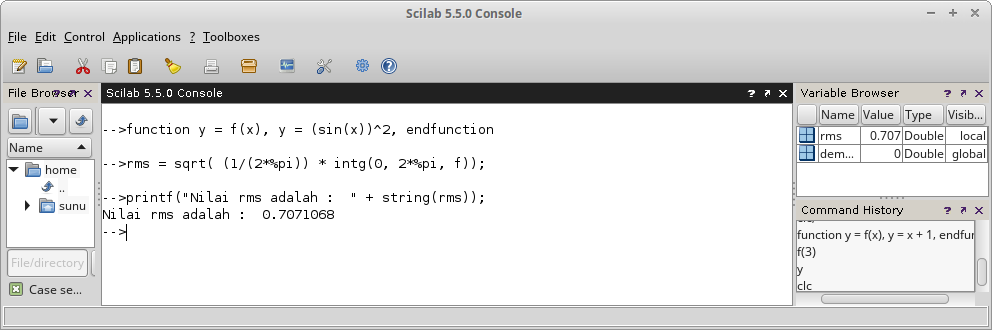 Gambar 22.
Gambar 22.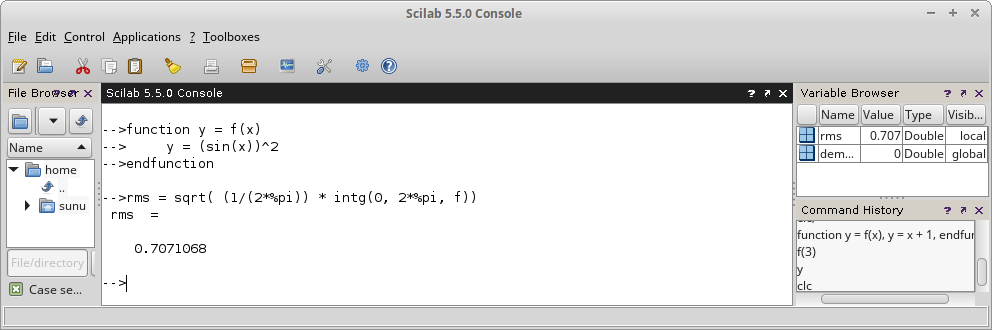 Gambar 23.
Gambar 23.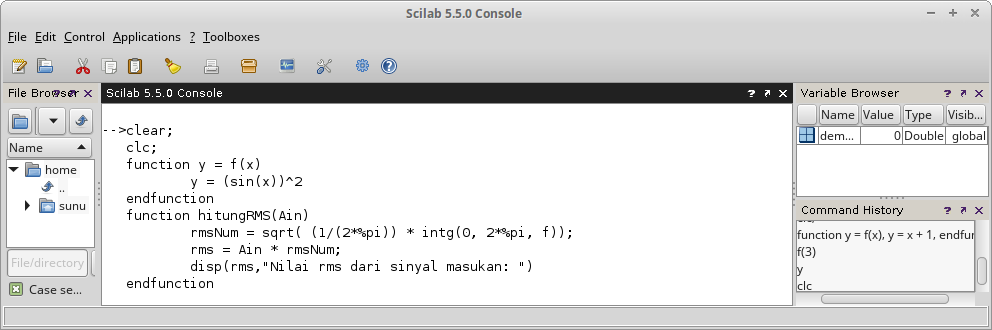 Gambar 24.
Gambar 24.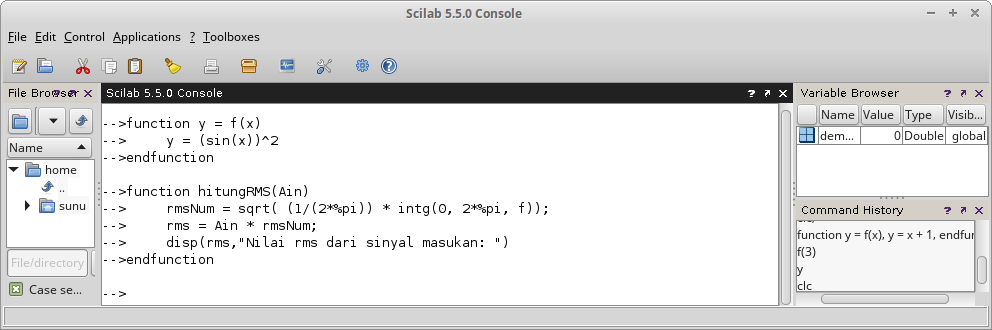 Gambar 25.
Gambar 25.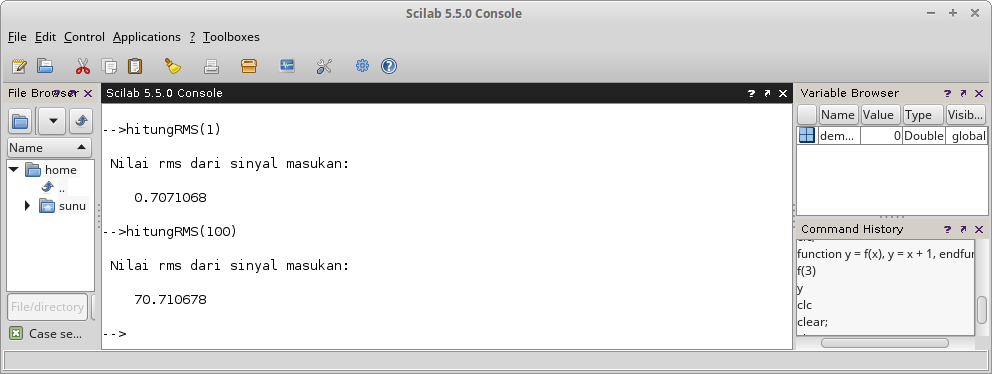 Gambar 26.
Gambar 26.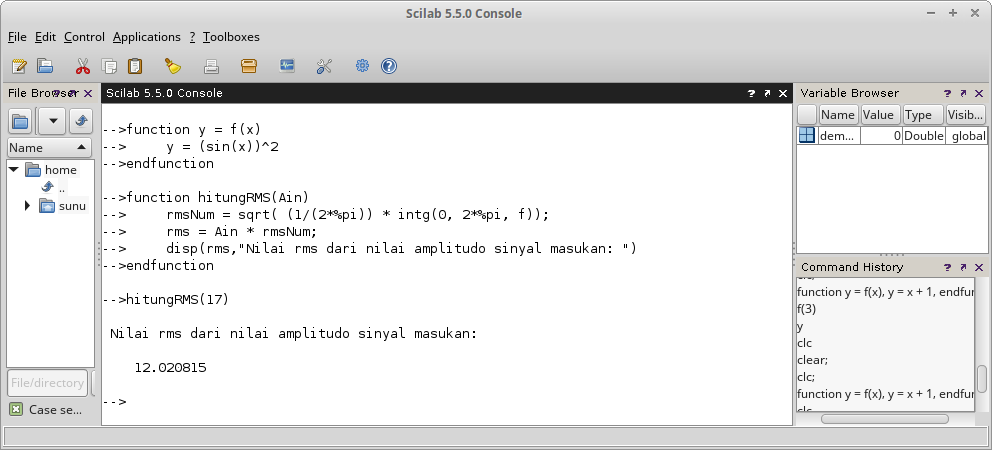 Gambar 27.
Gambar 27.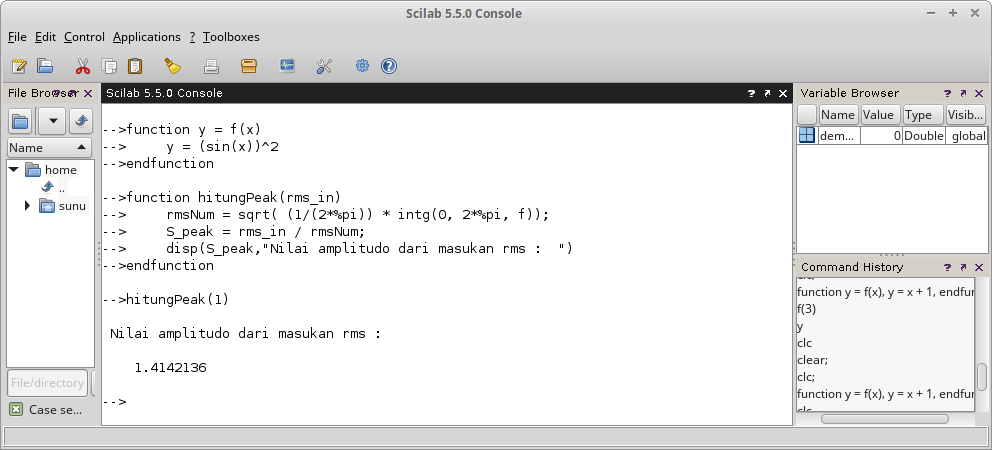 Gambar 28.
Gambar 28.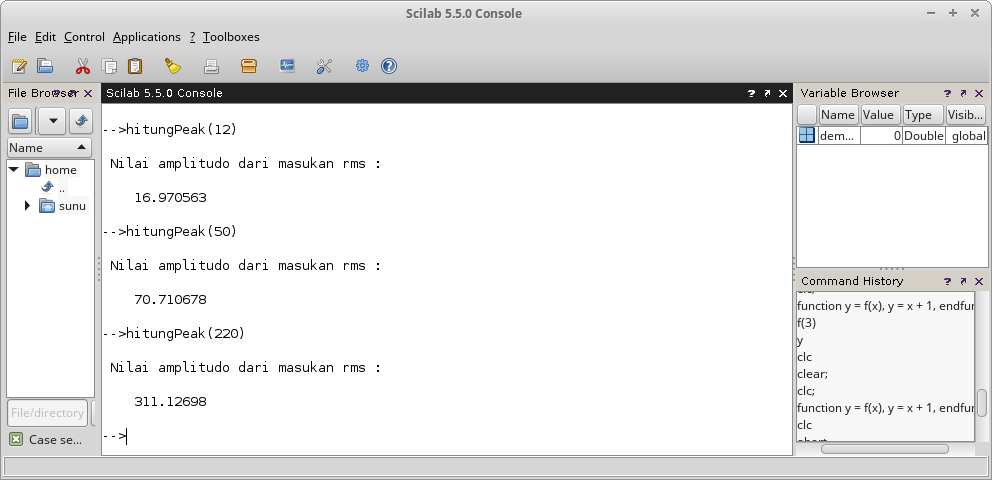 Gambar 29.
Gambar 29.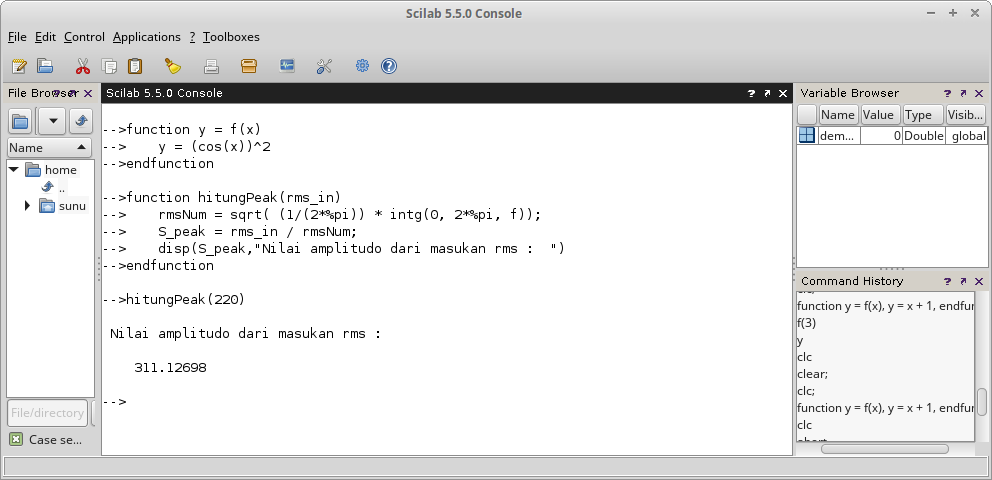 Gambar 30.
Gambar 30.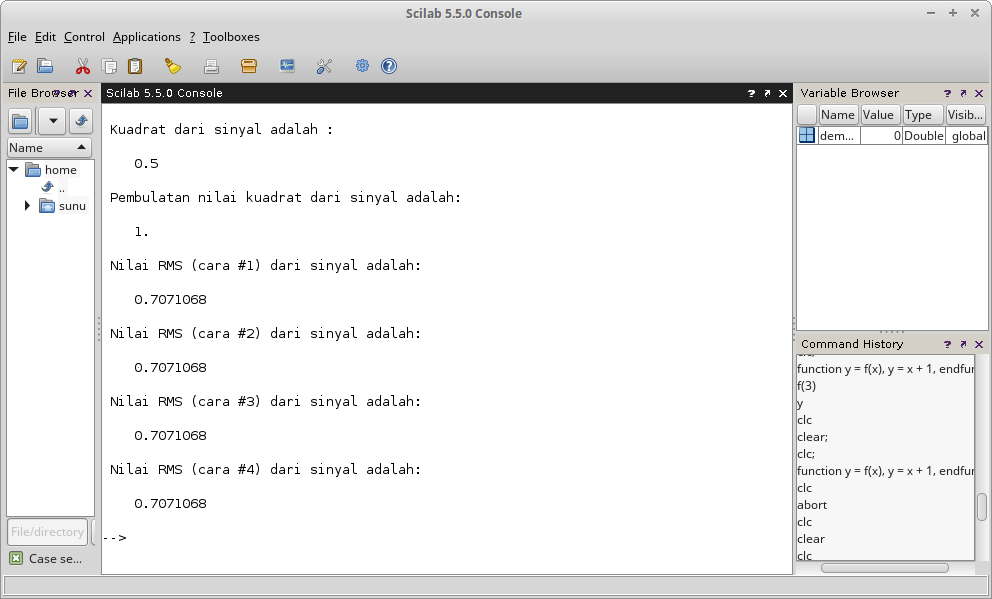 Gambar 31.
Gambar 31.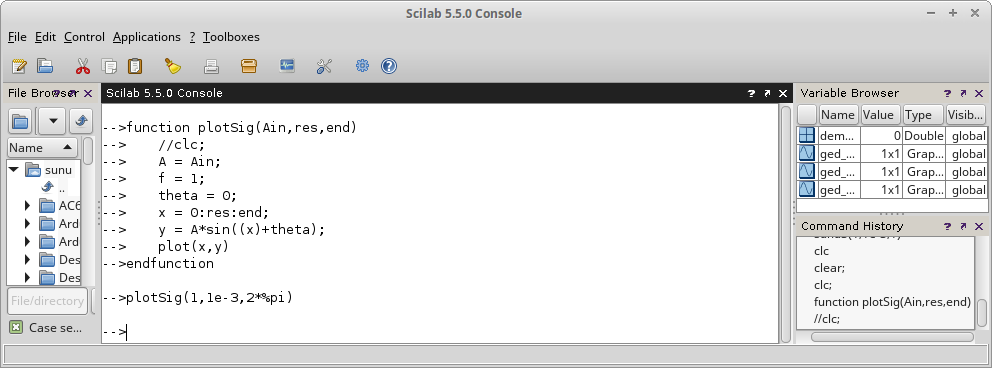 Gambar 32.
Gambar 32.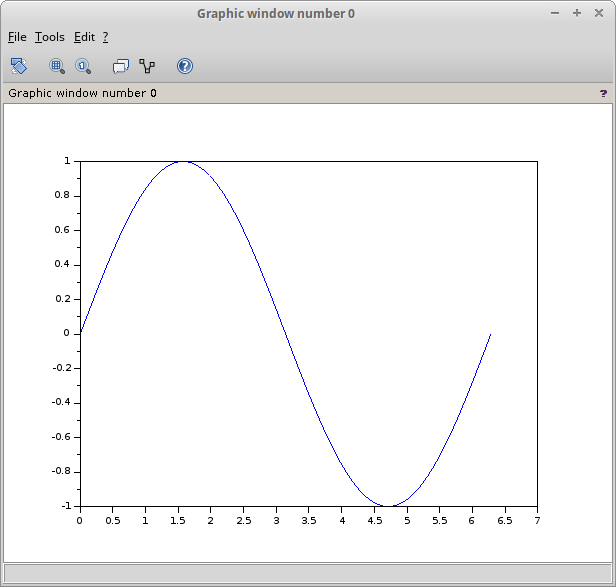 Gambar 33.
Gambar 33.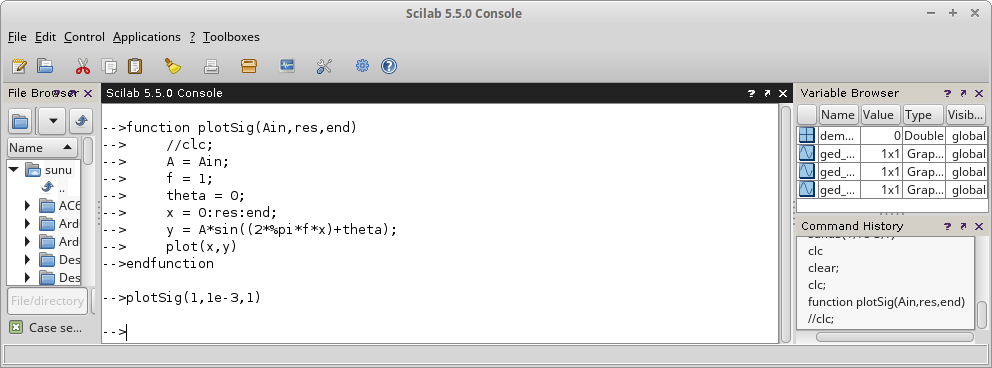 Gambar 34.
Gambar 34.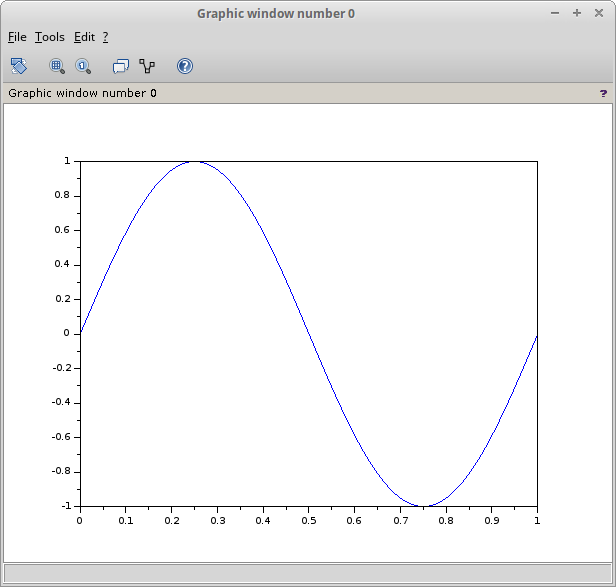 Gambar 35.
Gambar 35.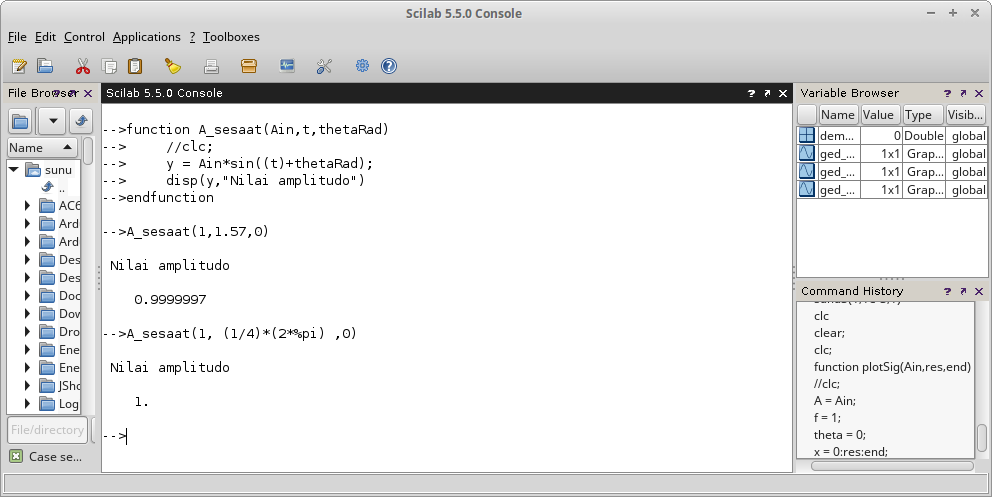 Gambar 36.
Gambar 36.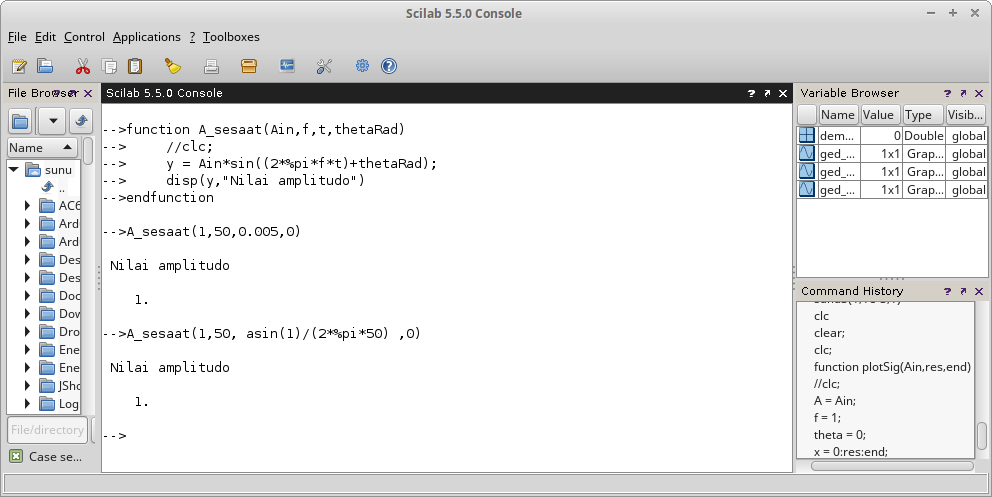 Gambar 37.
Gambar 37.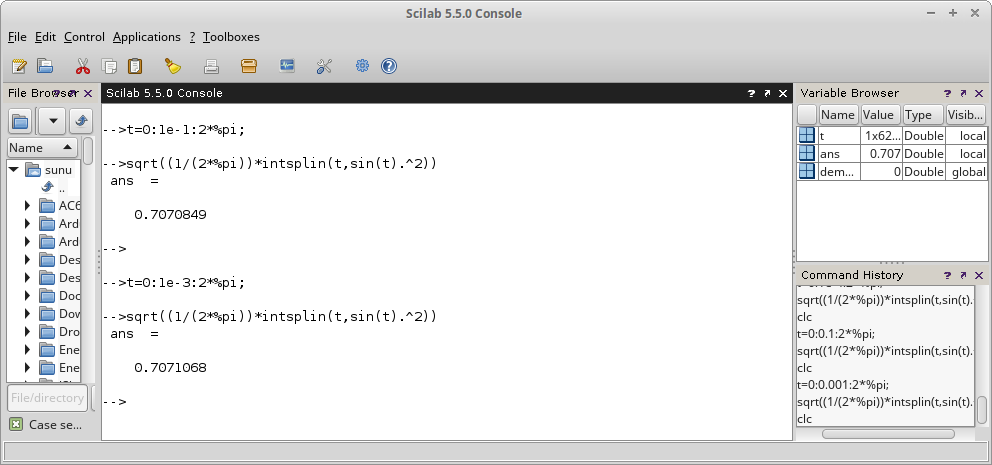 Gambar 38.
Gambar 38. Gambar 39. [/su_panel]
Gambar 39. [/su_panel]


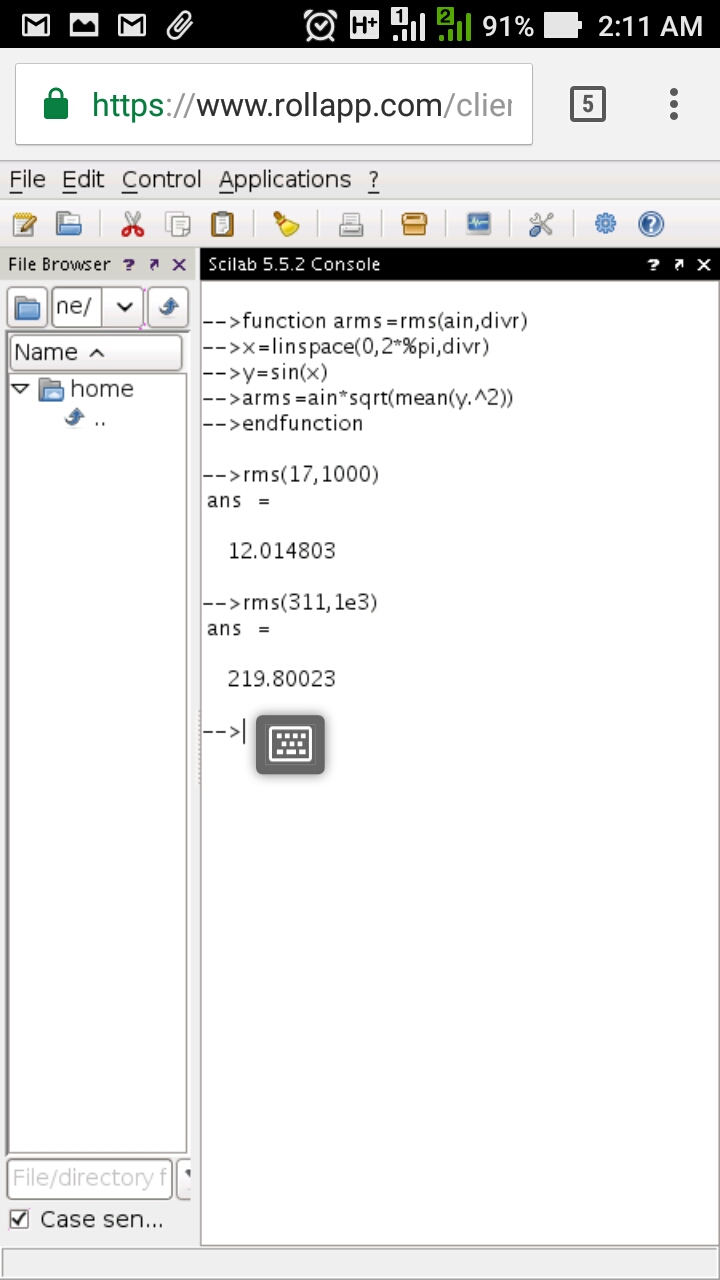





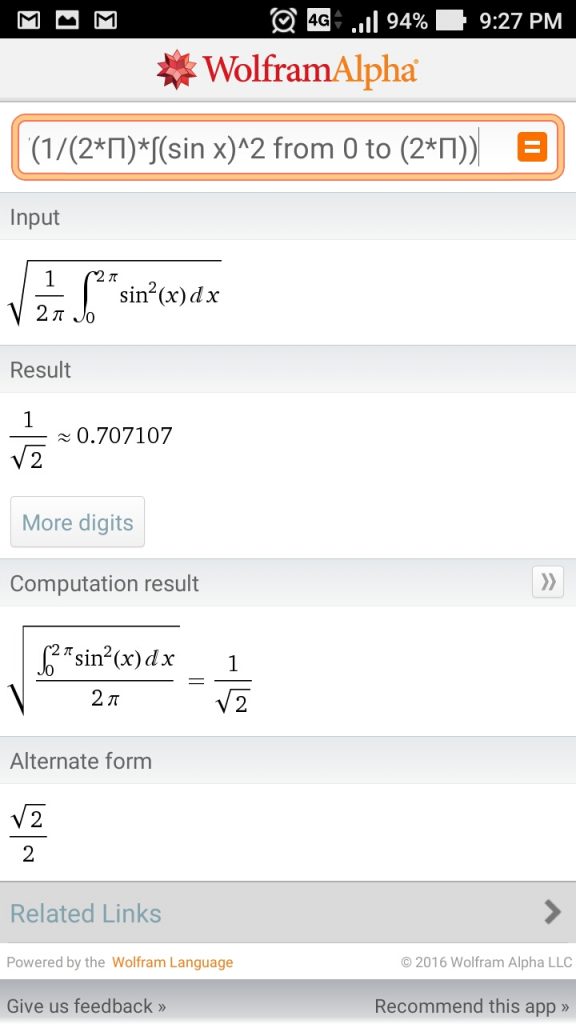
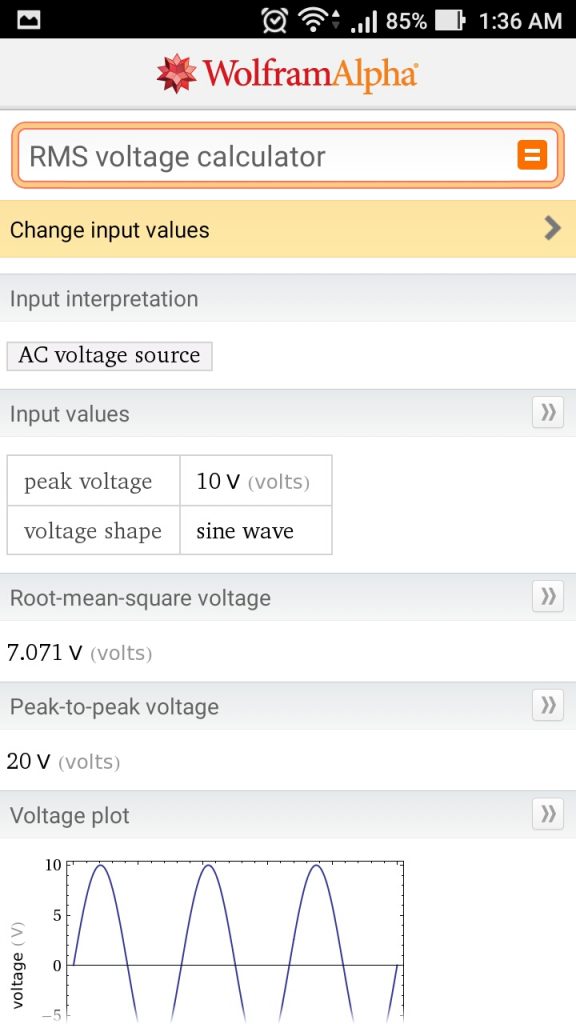
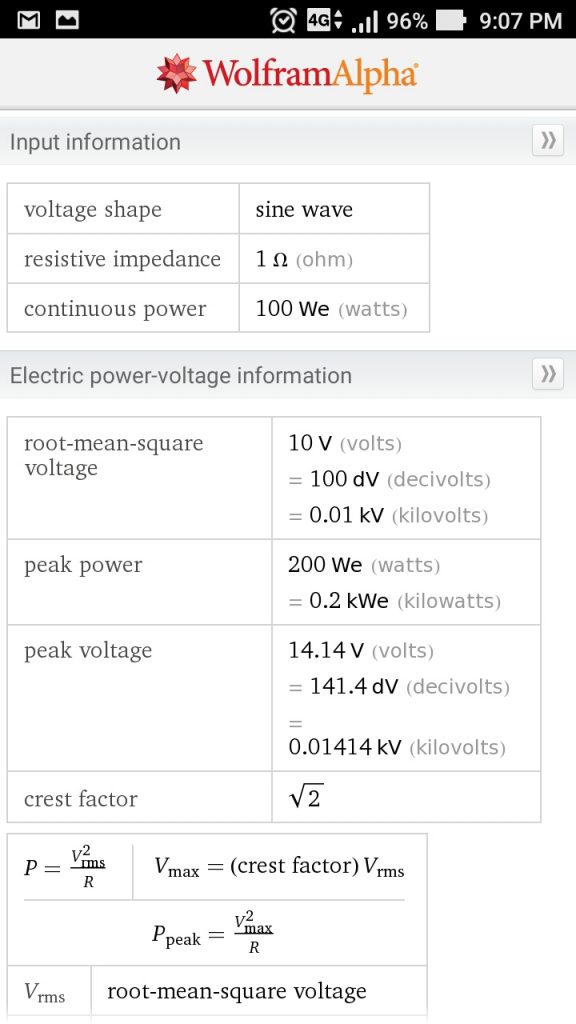
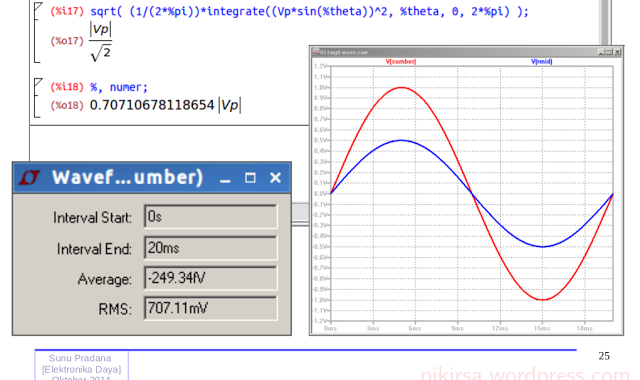

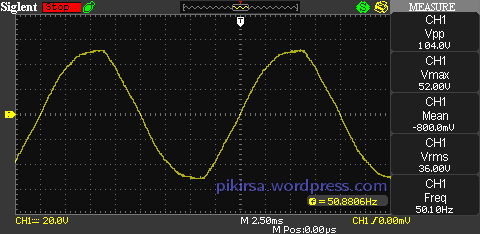 Gambar 1. Bentuk gelombang sinus tegangan A.C. memperlihatkan bentuk kurva yang tidak ideal.
Gambar 1. Bentuk gelombang sinus tegangan A.C. memperlihatkan bentuk kurva yang tidak ideal.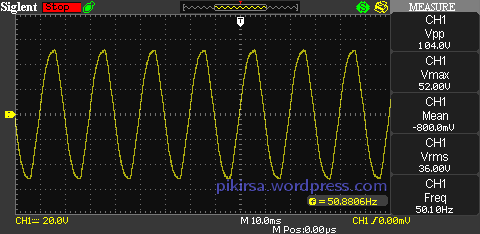 Gambar 2. Bentuk gelombang sinus tegangan A.C. dengan jumlah siklus yang lebih banyak.
Gambar 2. Bentuk gelombang sinus tegangan A.C. dengan jumlah siklus yang lebih banyak.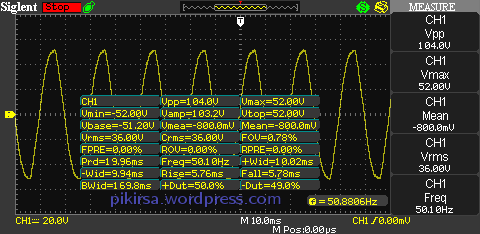 Gambar 3. Semua pengukuran numeris ditampilkan pada DSO.
Gambar 3. Semua pengukuran numeris ditampilkan pada DSO.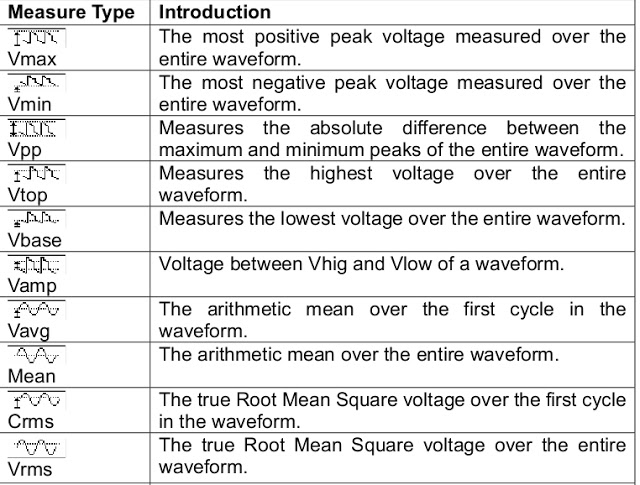 Gambar 4. Panduan untuk memahami definisi parameter pada Gambar 3.
Gambar 4. Panduan untuk memahami definisi parameter pada Gambar 3.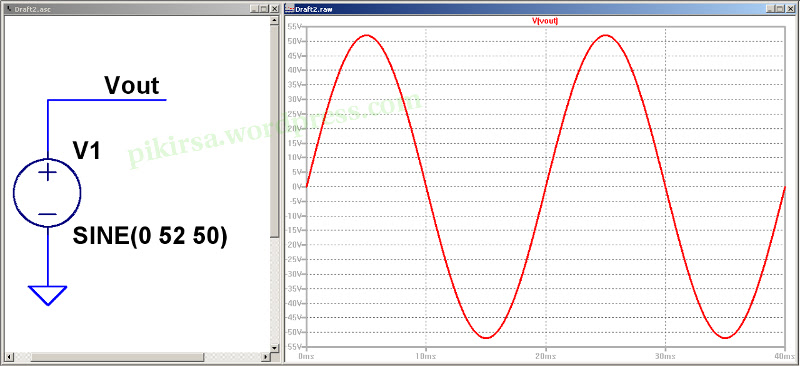 Gambar 5. Hasil simulasi dengan LTspice, Vp=52 Volt AC, frekuensi=50Hz.
Gambar 5. Hasil simulasi dengan LTspice, Vp=52 Volt AC, frekuensi=50Hz.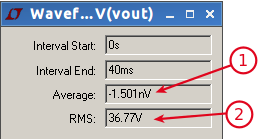 Gambar 6. Fasilitas di LTspice yang memungkinkan pengguna untuk mengetahui nilai rata-rata dan r.m.s.
Gambar 6. Fasilitas di LTspice yang memungkinkan pengguna untuk mengetahui nilai rata-rata dan r.m.s. Gambar 7. Dasar perhitungan nilai rata-rata gelombang sinus ideal.
Gambar 7. Dasar perhitungan nilai rata-rata gelombang sinus ideal. Gambar 8. Perhitungan untuk memperoleh nilai rata-rata setengah gelombang yang mewakili satu gelombang penuh.
Gambar 8. Perhitungan untuk memperoleh nilai rata-rata setengah gelombang yang mewakili satu gelombang penuh.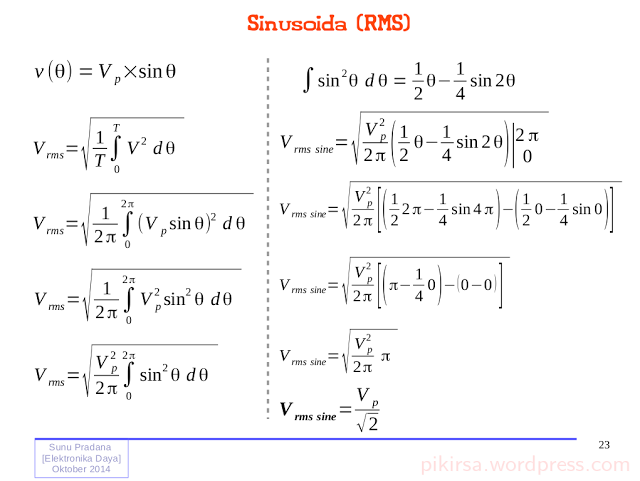 Gambar 9. Penyelesaian perhitungan integrasi untuk mendapatkan nilai RMS dari gelombang sinus satu siklus.
Gambar 9. Penyelesaian perhitungan integrasi untuk mendapatkan nilai RMS dari gelombang sinus satu siklus.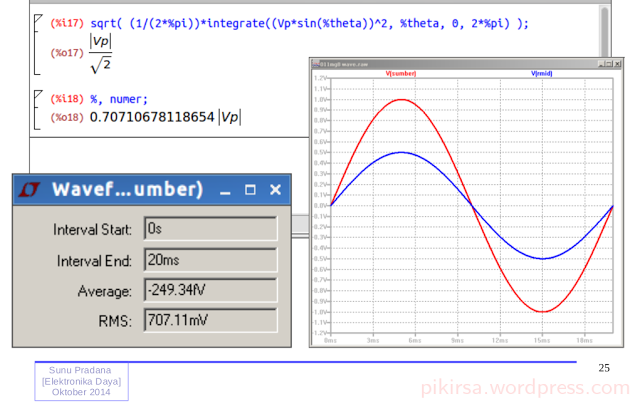 Gambar 11. Nilai RMS dengan contoh tegangan simulasi 1 V, normalisasi.
Gambar 11. Nilai RMS dengan contoh tegangan simulasi 1 V, normalisasi. Gambar 12. Contoh perhitungan pembuktian dengan kalkulator Algeo.
Gambar 12. Contoh perhitungan pembuktian dengan kalkulator Algeo. Gambar 13. Perhitungan nilai rata-rata untuk setengah gelombang dengan kalkulator biasa.
Gambar 13. Perhitungan nilai rata-rata untuk setengah gelombang dengan kalkulator biasa. Gambar 14. Perhitungan untuk nilai RMS gelombang sinus dengan hasil fraction.
Gambar 14. Perhitungan untuk nilai RMS gelombang sinus dengan hasil fraction. Gambar 15. Perhitungan nilai RMS untuk gelombang sinus dengan hasil desimal.
Gambar 15. Perhitungan nilai RMS untuk gelombang sinus dengan hasil desimal.