Salah satu bagian materi dari mata kuliah Elektronika Daya II adalah pelajaran mengenai buck converter. Dimulai dari penggambaran konverter ini secara umum, kemudian beberapa contoh simulasi rangkaian dasar buck converter. Lalu salah satu contoh implementasi IC pengendali komersial yang memiliki simulasi yang relatif mudah dipelajari, yaitu LT1074 dengan simulator LTspice. Beberapa cara pengujian konverter telah disampaikan di artikel tersebut. Di artikel berikutnya disampaikan bagaimana simulasi dapat dilakukan untuk memahami cara kerja dasar dari IC LM2596. Saat artikel ini ditulis, papan buck converter yang mempergunakan LM2596 jauh lebih banyak dijual di situs online lokal daripada IC LT1074. IC lain yang juga banyak dipergunakan adalah MP2307 yang sudah dibahas di artikel sebelum ini.
Di artikel ini akan disampaikan mengenai IC yang juga banyak dipakai di papan penurun tegangan yang banyak dijual di Indonesia, yaitu XL4005, XL4015 dan XL4016. Berbeda dengan LT1074, LM2596, dan MP2307, sampai hari ini saya belum menemukan simulator atau simulasi untuk ketiga IC XL**** dari XLSEMI tersebut. Sekalipun ada keterbatasan, di artikel ini akan coba fokus ke salah satu fitur kemudahan penggunakan IC semacam ini (yang juga mirip dengan sejumlah IC yang dibahas sebelumnya). Fitur itu adalah mengenai bagaimana rangkaian resistor pembagi tegangan sederhana dipakai sebagai sensor untuk menentukan nilai tegangan keluaran.
Untuk masing-masing datasheet dapat dilihat di web site komponen, tetapi secara ringkas dapat ditampilkan di sini:
- XL4005: 5A 300KHz 32V Buck DC to DC Converter. [cadangan link]
- XL4015: 5A 180KHz 36V Buck DC to DC Converter. [cadangan link]
- XL4016: 12A 180KHz 40V Buck DC to DC Converter. [cadangan link]
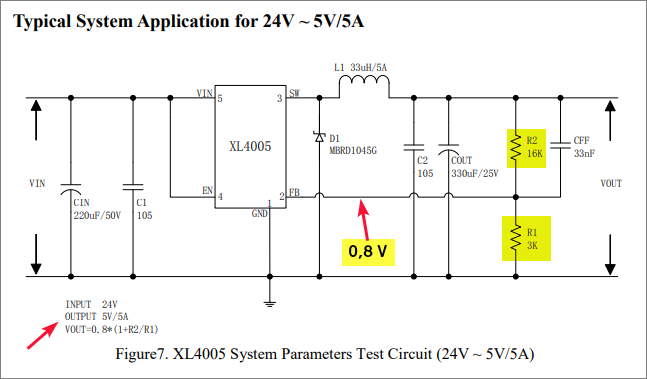 Gambar 1.
Gambar 1.
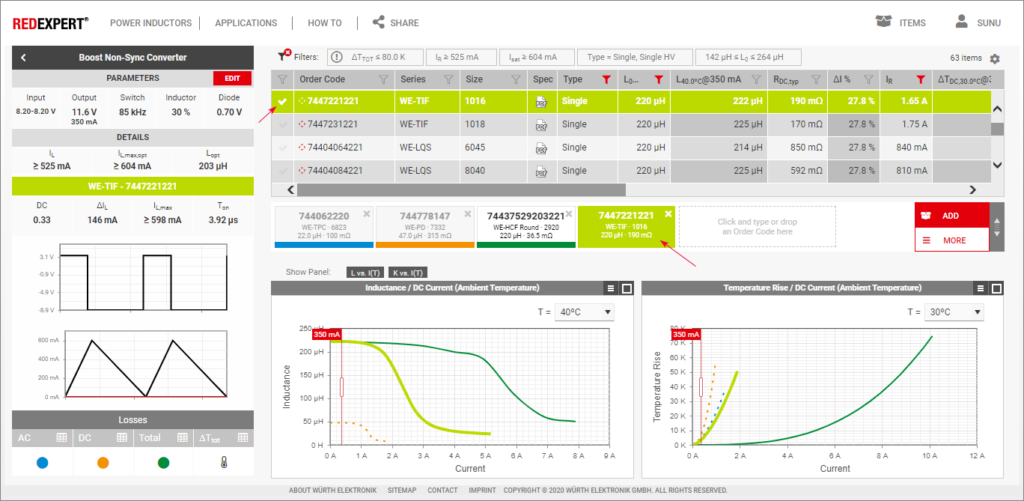
Gambar 1 adalah contoh salah satu bentuk penggunaan IC XL4005 yang umum (typical) ini bisa menjadi semacam template bagi keperluan sejenis. Di sini semua resistor yang dipergunakan adalah yang bertipe tetap dan bukan potensiometer. Dengan pembagi tegangan R1 dan R2, saat nilai tegangan keluaran bernilai 5 V maka di node FB akan ada tegangan sebesar 0,8 V (0,789 V). Dengan kata lain, kita bisa menentukan nilai tegangan yang diturunkan di sisi keluaran berdasarkan persamaan (lihat panah).
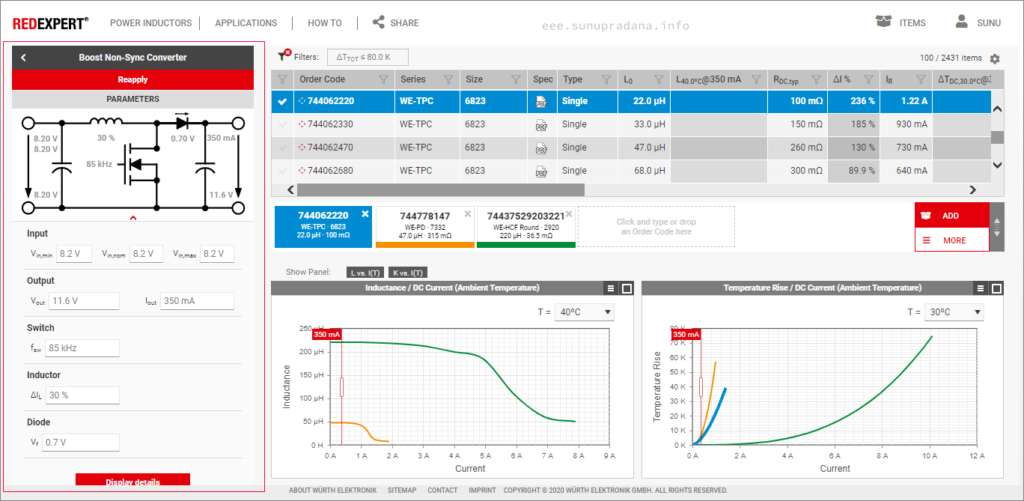
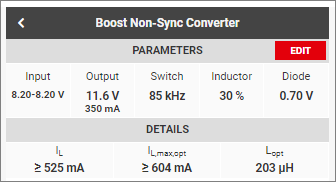
Perhitungan bisa dilakukan manual, dengan kalkulator elektronik, atau dengan perangkat lain yang sesuai. Sebagai contoh adalah fasilitas perhitungan online di Gambar 2.
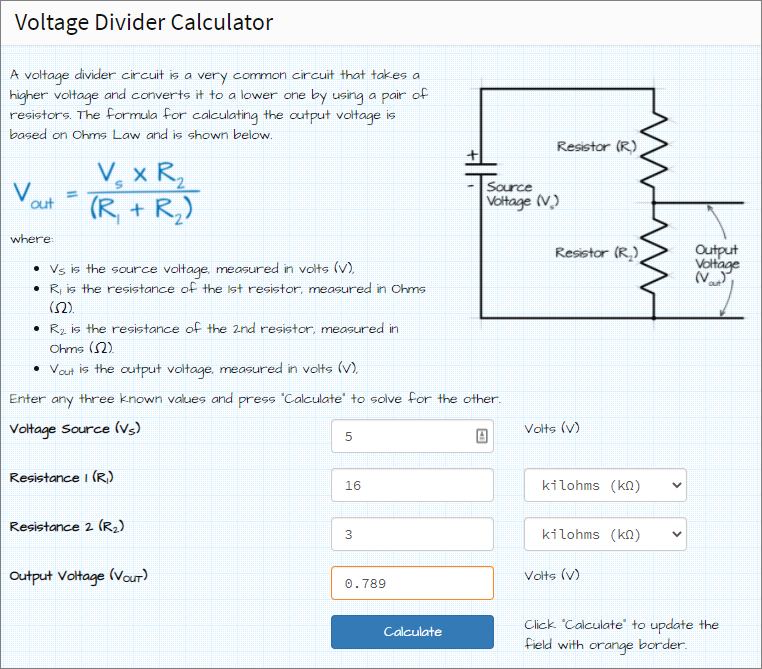 Gambar 2.
Gambar 2.
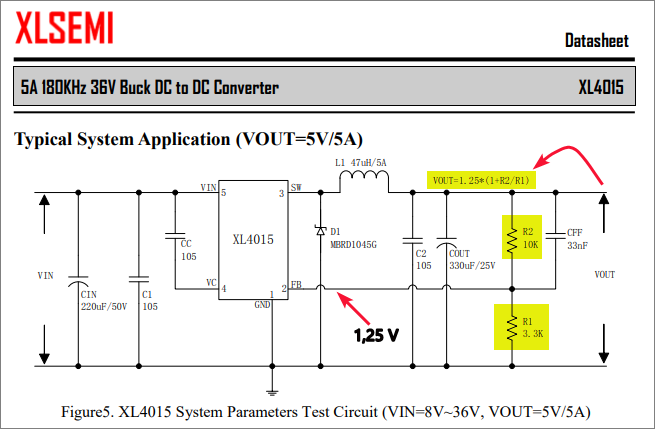 Gambar 3. Contoh rangkaian XL4015.
Gambar 3. Contoh rangkaian XL4015.
Nilai feedback threshold voltage untuk XL4015 adalah 1,25 V, sebagaimana terlihat pada Gambar 3.
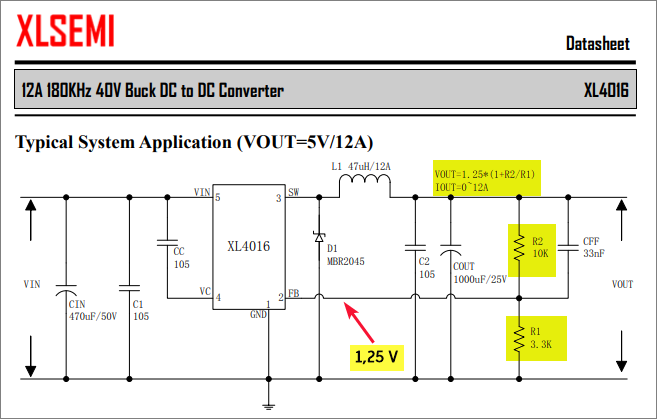 Gambar 4. Contoh rangkaian XL4016.
Gambar 4. Contoh rangkaian XL4016.
Dari ketiga gambar contoh konfigurasi rangkaian ini bisa dilihat peran penting resistor pembagi tegangan sebagai sensor. Bahkan seandainya pun produsen papan sistem mempergunakan potensiometer. Semoga ini bisa jadi salah satu inspirasi belajar. Bahwa hal yang sederhana tetapi sesungguhnya fundamental itu akan sangat mungkin tetap terus terpakai di sistem yang lebih kompleks. Dengan begitu pelajaran yang sepintas sederhana tidak baik untuk dianggap remeh, hanya karena pelajar belum cukup punya pengetahuan atau wawasan manfaat yang dipelajari di kemudian hari.
PCB
 Gambar 5. Contoh papan buck converter demgam XL4005 dari Sunrom.
Gambar 5. Contoh papan buck converter demgam XL4005 dari Sunrom.
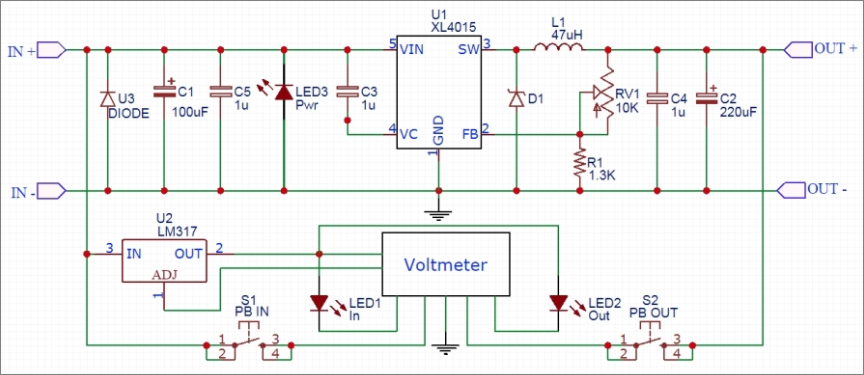 Gambar 6. Skematik rangkaian penurun tegangan dengan XL4015 (link).
Gambar 6. Skematik rangkaian penurun tegangan dengan XL4015 (link).
 Gambar 7. Contoh papan buck converter dengan XL4015 (link).
Gambar 7. Contoh papan buck converter dengan XL4015 (link).
Gambar 6 adalah salah salah satu bentuk rangkaian penurun tegangan yang mempergunakaan IC XL4015. Skema ini diwujudkan dalam bentuk papan komersial di Gambar 7.
Di Gambar 6 terdapat satu IC catu daya linier, yaitu LM317. Ini adalah satu contoh di antara cukup banyak contoh bagaimana sistem catu daya linier digunakan bersama dalam satu sistem dengan catu daya tersakelar (switching). Karena itu di dalam perkuliahan elektronika daya, kedua jenis catu daya dipelajari karena masih diperlukan hingga sampai saat ini.
 Gambar 8. [Sumber: link]
Gambar 8. [Sumber: link]
Gambar 8 adalah papan buck converter yang harganya lebih murah dari papan pada Gambar 7. Salah satu contoh penerapan dari papan penurun tegangan di Gambar 8 diperlihatkan di Gambar 9. Keterangan lebih lanjut bisa dibaca di situs aslinya.
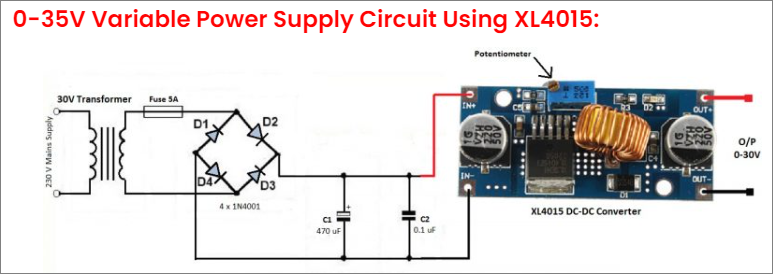 Gambar 9. [Sumber: link]
Gambar 9. [Sumber: link]
 Gambar 10. [Sumber: link]
Gambar 10. [Sumber: link]
Gambar 11. [Sumber: link]
 Gambar 12. [Sumber: link]
Gambar 12. [Sumber: link]
Gambar 10 adalah desain dasar rangkaian XL4015 dengan kemampuan pembatasan nilai tegangan dan arus. Gambar 11 dan Gambar 12 adalah perwujudan dari skema dasar di Gambar 10. Menarik untuk dilihat bahwa bahkan untuk catu daya tersakelar terdapat kebutuhan untuk masih mempergunakan komonen catu daya linier, yaitu 78L05 untuk memberi tegangan ke komponen LM358 dan sebagai bagian untuk referensi tegangan. Keterangan lebih lanjut dapat dibaca di halaman artikel sumber.
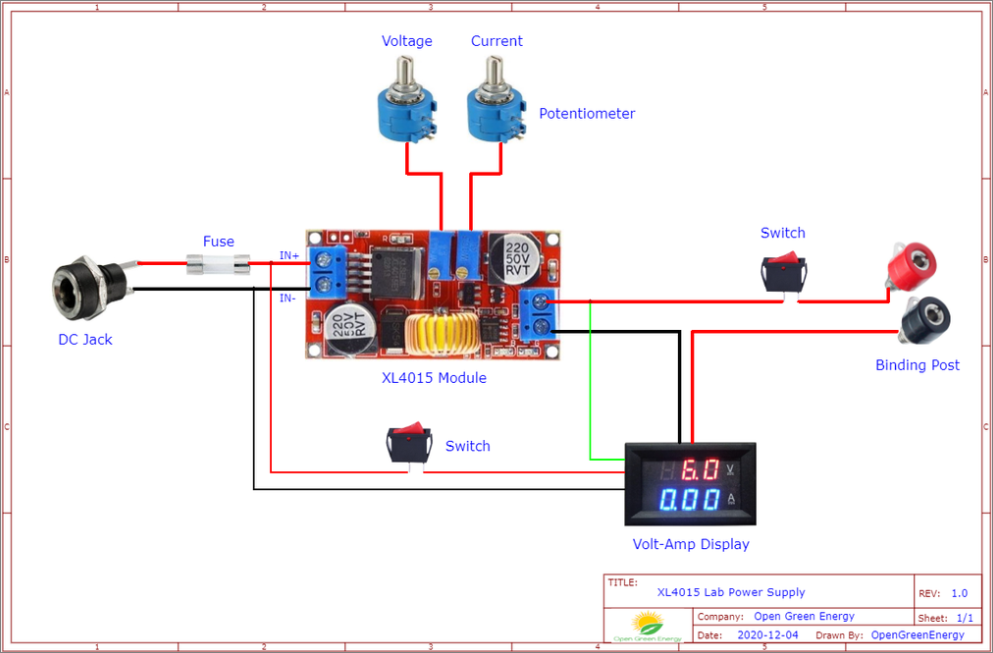 Gambar 13. Rangkaian XL4015 untuk catu daya.
Gambar 13. Rangkaian XL4015 untuk catu daya.
 Gambar 14. Contoh pemanfaatan buck converter XL4015.
Gambar 14. Contoh pemanfaatan buck converter XL4015.
Gambar 13 dan Gambar 14 adalah contoh bagaimana rangkaian XL4015 dapat dipergunakan sebagai catu daya sederhana untuk laboratorium.

Gambar 15. Contoh papan buck converter dengan IC XL4016.
 Gambar 16. Contoh papan buck converter dengan IC XL4016.
Gambar 16. Contoh papan buck converter dengan IC XL4016.
Gambar 15 dan Gambar 16 adalah contoh papan sistem penurun tegangan dengan kemampuan yang lebih besar. Semakin besar panas yang dihasilkan maka diperlukan keping pendingin yang lebih besar. Sekalipun catu daya tersakelar secara umum lebih efisien untuk daripada catu daya linier yang sekelas, tetapi tetap saja menghasilkan panas yang perlu diatasi.
Unjuk kerja dan pengujian
Gambar 17. Cuplikan screenshot gambar tabel masukan dan keluaran rangkaian XL4015.
Gambar 18. Gambar tangkapan riak di keluaran XL4015.
Untuk pengujian dalam bentuk video, dapat disaksikan langsung melalui playlist di YouTube.

 Gambar 1.
Gambar 1.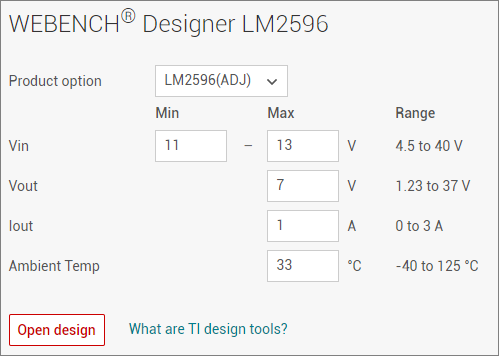 Gambar 2.
Gambar 2.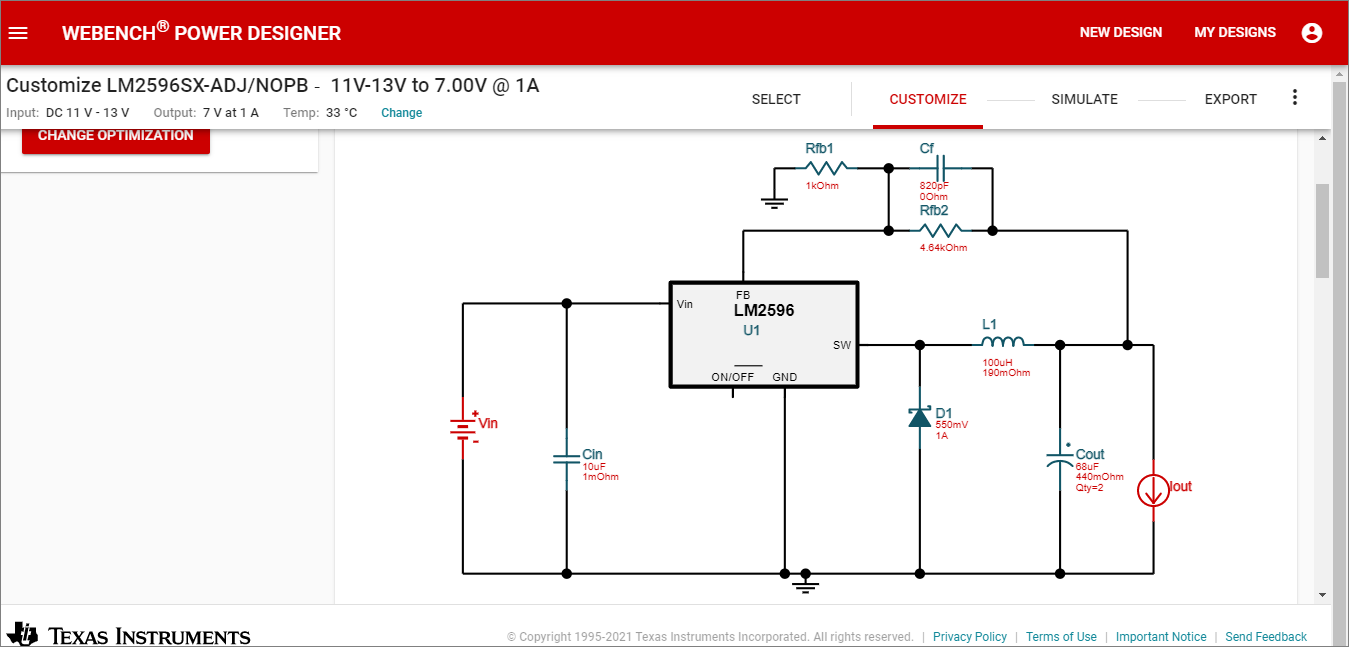 Gambar 3.
Gambar 3.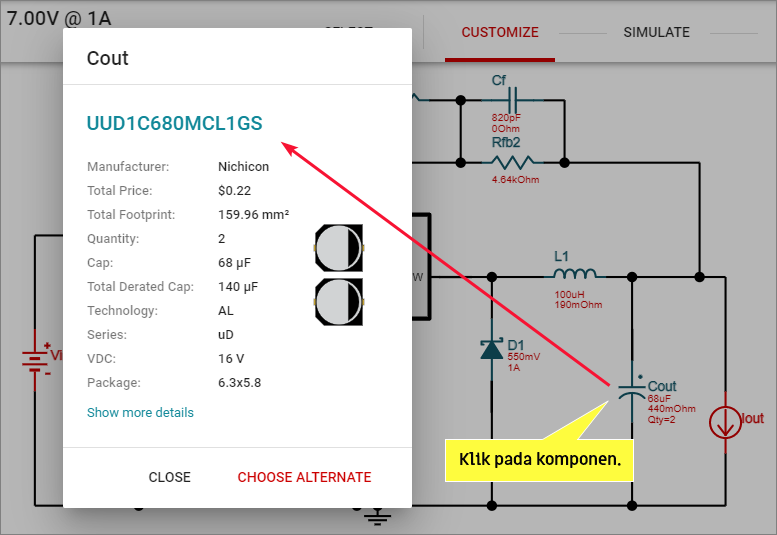 Gambar 4.
Gambar 4.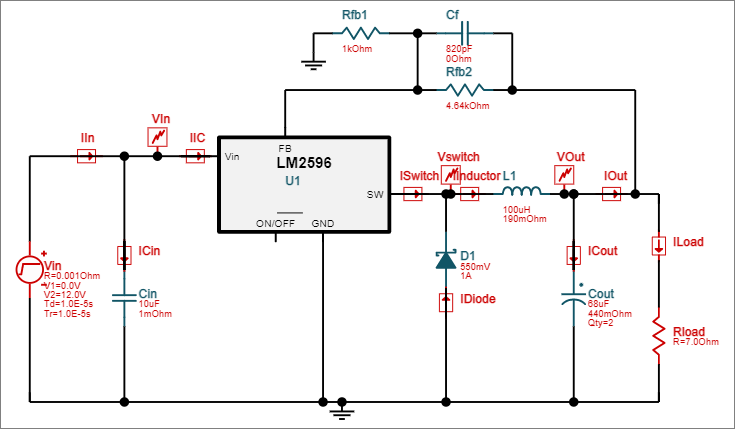 Gambar 5. Pilihan simulasi untuk kondisi startup.
Gambar 5. Pilihan simulasi untuk kondisi startup.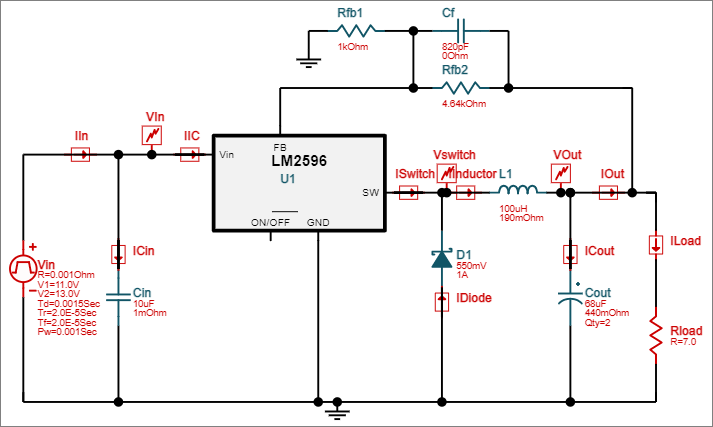 Gambar 6. Pilihan simulasi untuk kondisi input transient.
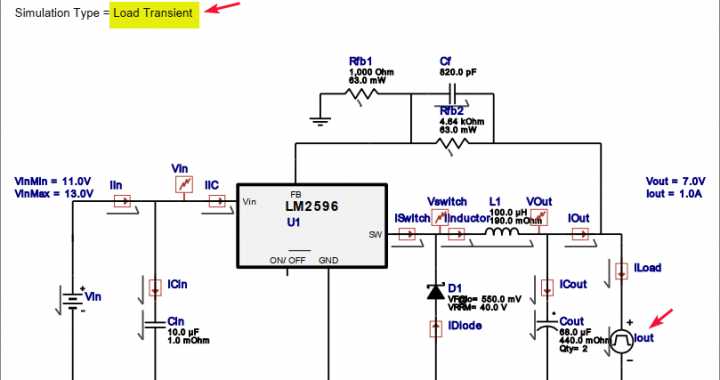
Gambar 6. Pilihan simulasi untuk kondisi input transient.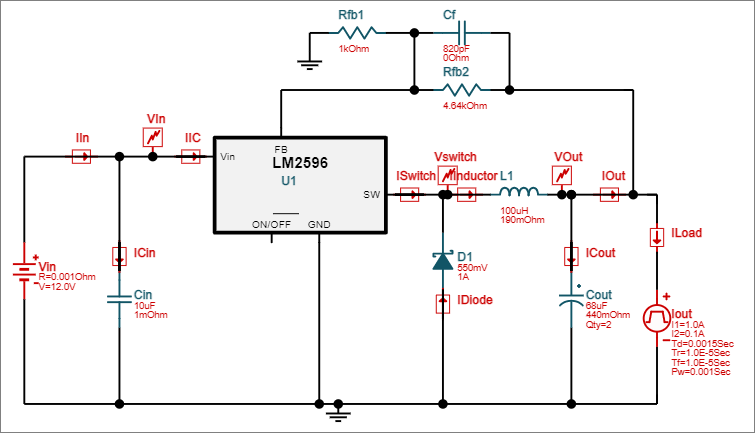 Gambar 7. Pilihan simulasi untuk kondisi load transient.
Gambar 7. Pilihan simulasi untuk kondisi load transient.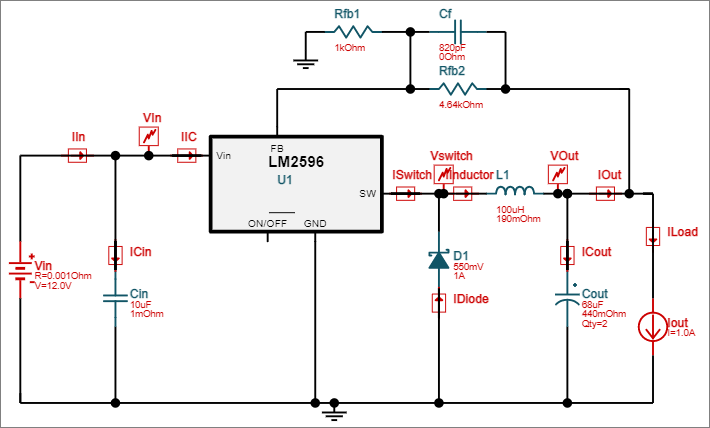 Gambar 8. Pilihan simulasi untuk kondisi steady state.
Gambar 8. Pilihan simulasi untuk kondisi steady state.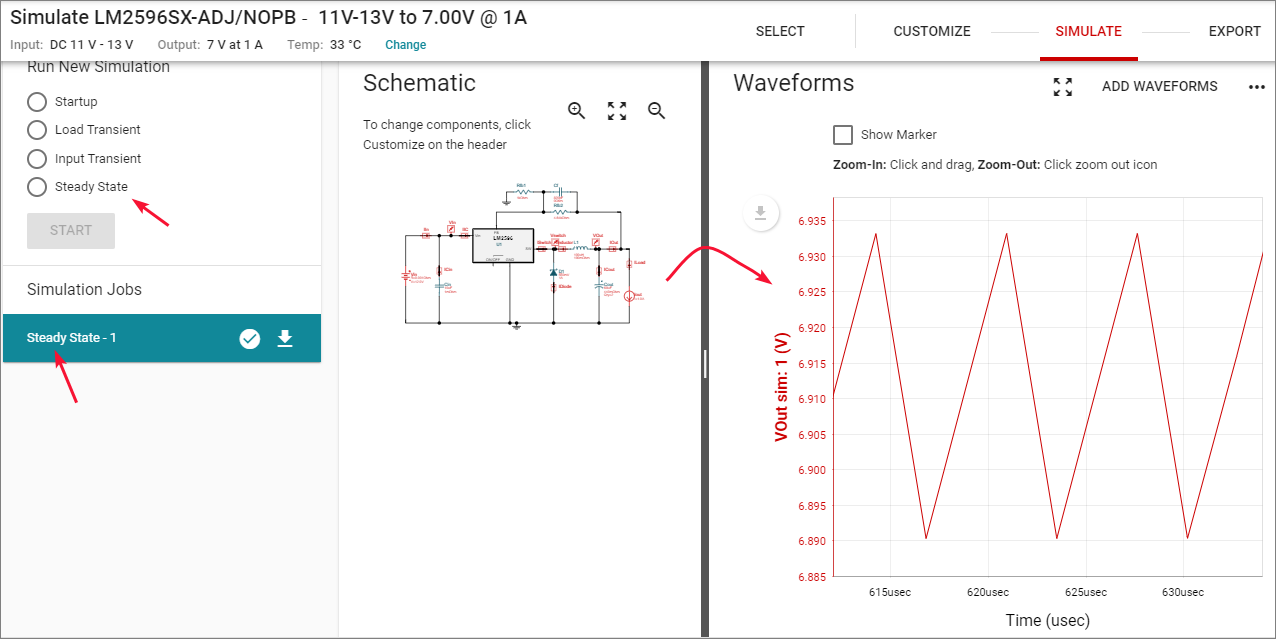 Gambar 9. Contoh hasil simulasi untuk kondisi steady state.
Gambar 9. Contoh hasil simulasi untuk kondisi steady state. Gambar 10.
Gambar 10.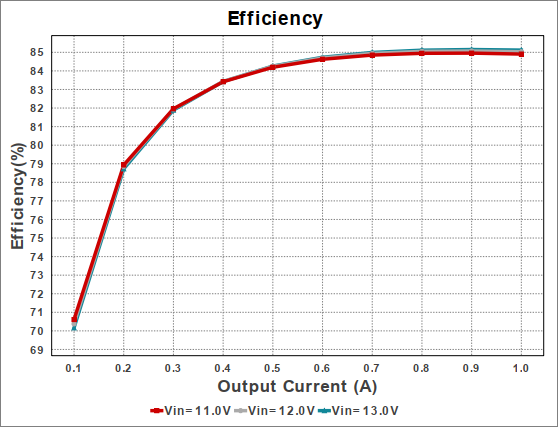 Gambar 11.
Gambar 11.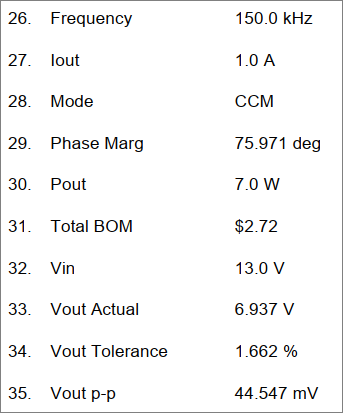 Gambar 12.
Gambar 12.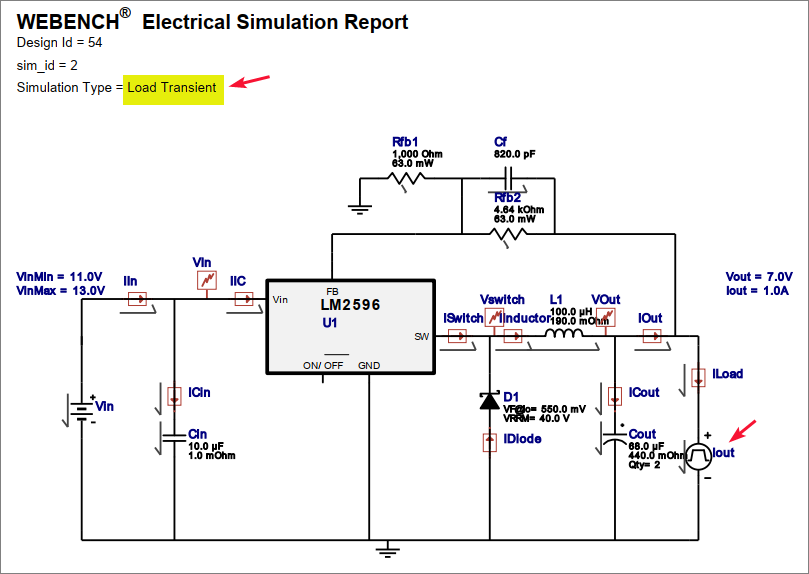 Gambar 13. Load transient simulation repot (PDF).
Gambar 13. Load transient simulation repot (PDF).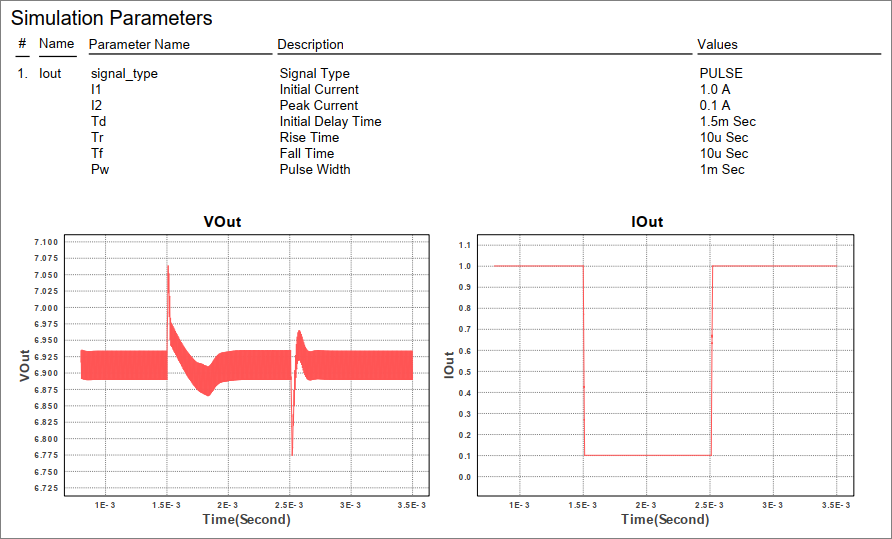 Gambar 14. Load transient simulation repot (PDF).
Gambar 14. Load transient simulation repot (PDF). Gambar 15. Contoh rancangan PCB.
Gambar 15. Contoh rancangan PCB.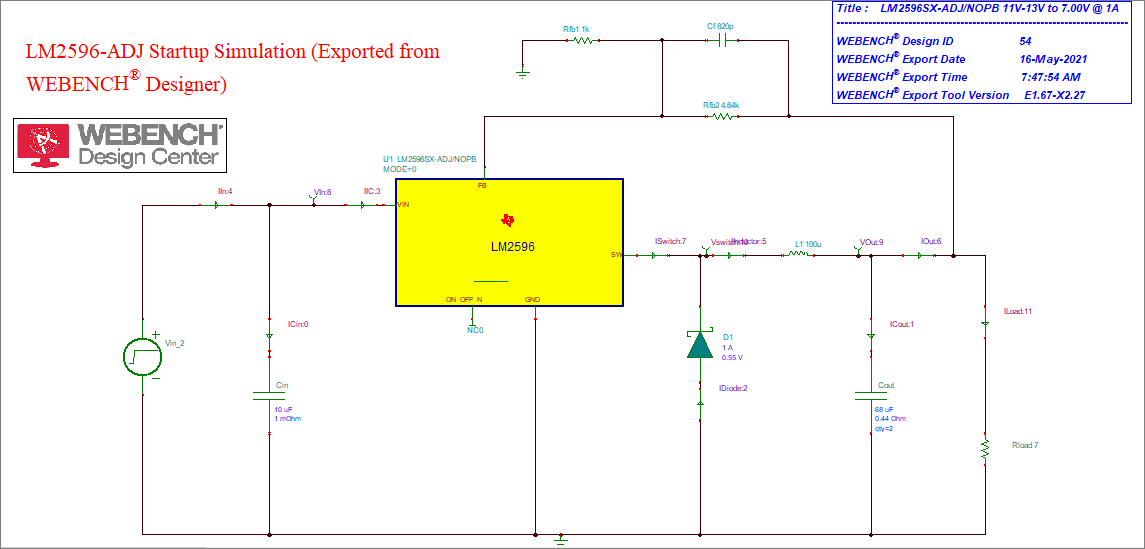 Gambar 16. Hasil ekspor dari Webench dapat dipilih untuk disimulasikan di TINA-TI.
Gambar 16. Hasil ekspor dari Webench dapat dipilih untuk disimulasikan di TINA-TI.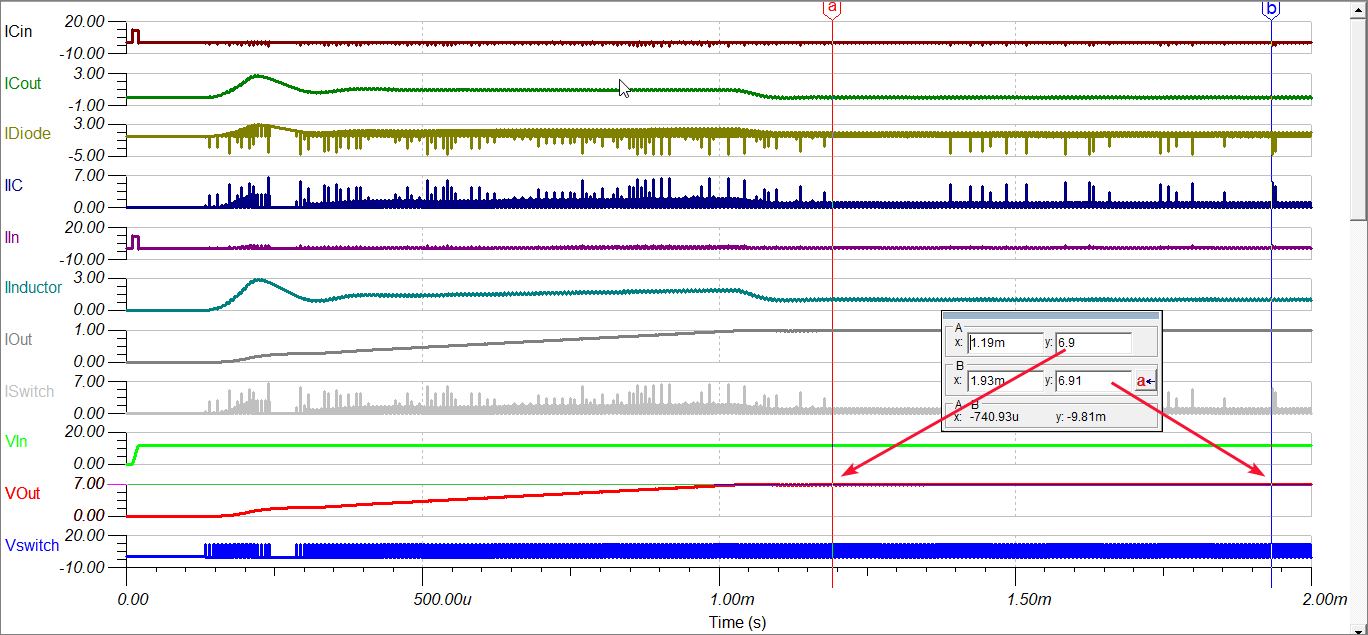 Gambar 17. Hasil simulasi di TINA-TI.
Gambar 17. Hasil simulasi di TINA-TI. Gambar 20. Skema rangkaian LM2596 untuk tegangan keluaran yang dapat diatur (
Gambar 20. Skema rangkaian LM2596 untuk tegangan keluaran yang dapat diatur ( Gambar 21. Produk jadi dari skema rangkaian LM2596 (
Gambar 21. Produk jadi dari skema rangkaian LM2596 (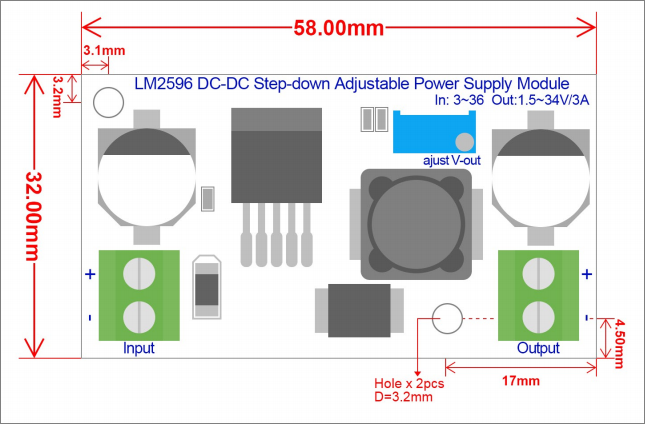 Gambar 22. Papan buck converter LM2596 produksi
Gambar 22. Papan buck converter LM2596 produksi  Gambar 23. Papan buck converter LM2596 produksi
Gambar 23. Papan buck converter LM2596 produksi  Gambar 24. Hasil pengujian thermal (
Gambar 24. Hasil pengujian thermal (

 Gambar 1. Landline telephone
Gambar 1. Landline telephone