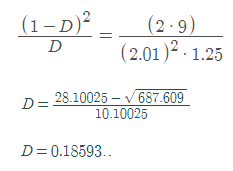Artikel ini adalah artikel keempat dari seri artikel mengenai flyback converter. Telah dicoba secara sistematis untuk membangun pemahaman tentang dasar operasi flyback topology di bagian power stage dimulai dari memaparkan tentang peran magnetizing inductance. Kemudian disampaikan mengenai bagaimana suatu flyback converter bekerja, berdasarkan operasi penyakelaran. Bahasan kedua ini bisa disampaikan karena diasumsukan mahasiswa telah membaca bagian pertama tentang kekhususan flyback transformer. Kemudian berbekal pemahaman tentang peran flyback transformer sebagai penyimpan energi sementara dan cara penyakelaran flyback converter, bahasan dilanjutkan ke tahapan persamaan dan perhitungan yang menggambarkan lebih detail tentang operasi suatu flyback converter power stage. Di artikel ketiga dipaparkan berbagai sumber yang memberi contoh perhitungan perancangan dan perhitungan yang memberi deskripsi operasi suatu flyback converter.
Maka di artikel ini akan disampaikan contoh-contoh simulasi flyback converter. Baik yang berupa power stage/open loop maupun simulasi satu flyback converter yang utuh dengan IC regulatornya.
[ Semua gambar di bawah ini dapat dilihat versi tampilan yang lebih besar dengan cara melakukan klik-kanan di gambar lalu memilih “Open image in new tab” pada browser. ]
Di bagian pertama ini saya menyampaikan contoh simulasi yang masih termasuk relatif paling mudah ditemui tetapi juga sudah termasuk sistem yang utuh. Contoh diambil dari simulator LTspice dengan produk IC regulator dari Linear Technology (perusahaan itu telah dibeli oleh perusahaan Analog Devices).
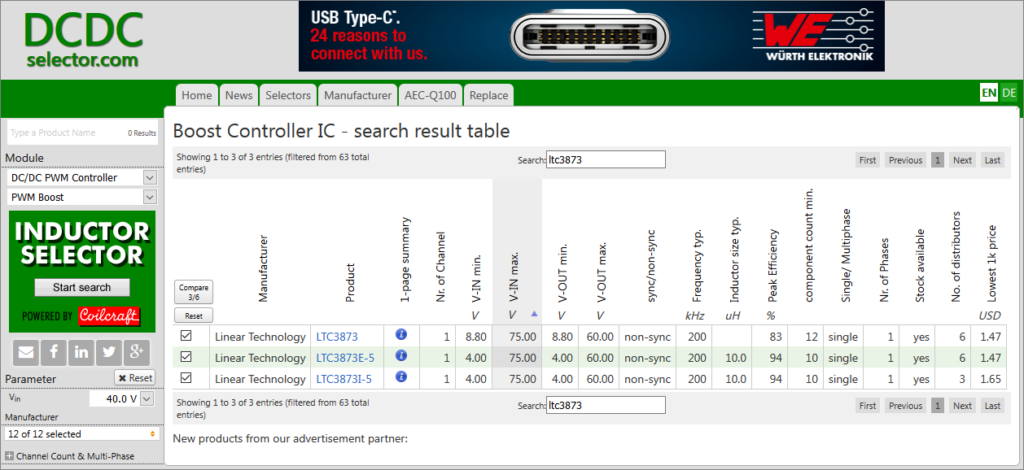Gambar 1. Pencarian IC LTC3873 untuk perbandingan.
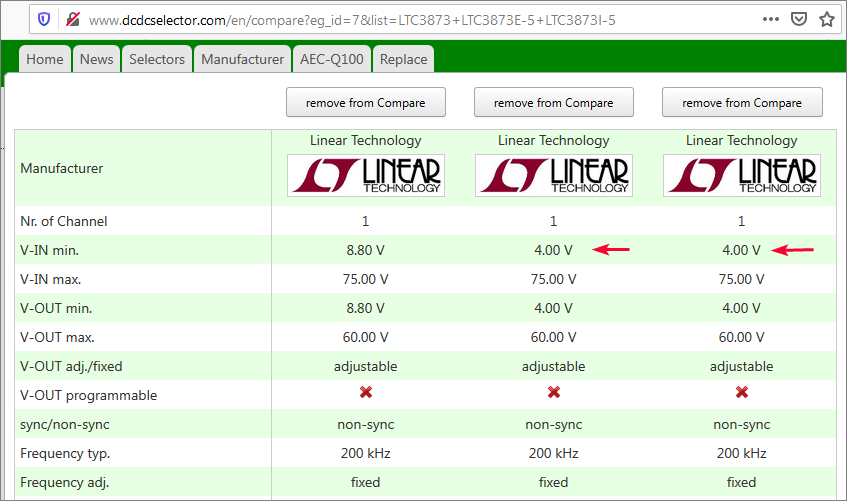Gambar 2. Perbandingan varian LTC3873.
Gambar 3. Website LTC3873-5.
Untuk mahasiswa sangat disarankan mengunjungi langsung halaman produk di website perusahaan produsen untuk keperluan desain akhir, seperti di Gambar 3. Biasanya di halaman seperti itu ada beberapa dokumen yang dapat dipakai untuk membantu proses belajar/memahami. Juga ada beberapa software/model yang bisa dipakai untuk melakukan simulasi. Juga sebaiknya mengunduh langsung datasheet dari situs produsen, terkecuali untuk komponen legacy. Di Gambar 4, adalah contoh datasheet yang bisa dipakai.
Gambar 4. Datasheet / Data sheet LTC3873-5.
Simulasi untuk IC LTC3873 maupun untuk IC LTC3873-5 telah disedikan oleh produsen di LTspice. Kita hanya perlu membukanya, tetapi ada sedikit masalah…
Gambar 5. Simulasi default untk LTC3873-5.
Jika anda buka simulasi seperti di Gambar 5, maka nanti yang akan tampil adalah simulasi IC tersebut untuk topoogi boost converter. Karena sebagaimana telah disebut di datasheet, IC ini bisa dipakai untuk beberapa topologi yang berbeda. Sebagai solusi cepat untuk melihat simulasi kerja suatu flyback converter, anda pilih IC LTC3873 (3873.asc), yang berada tepat di atasnya di contoh Gambar 5.
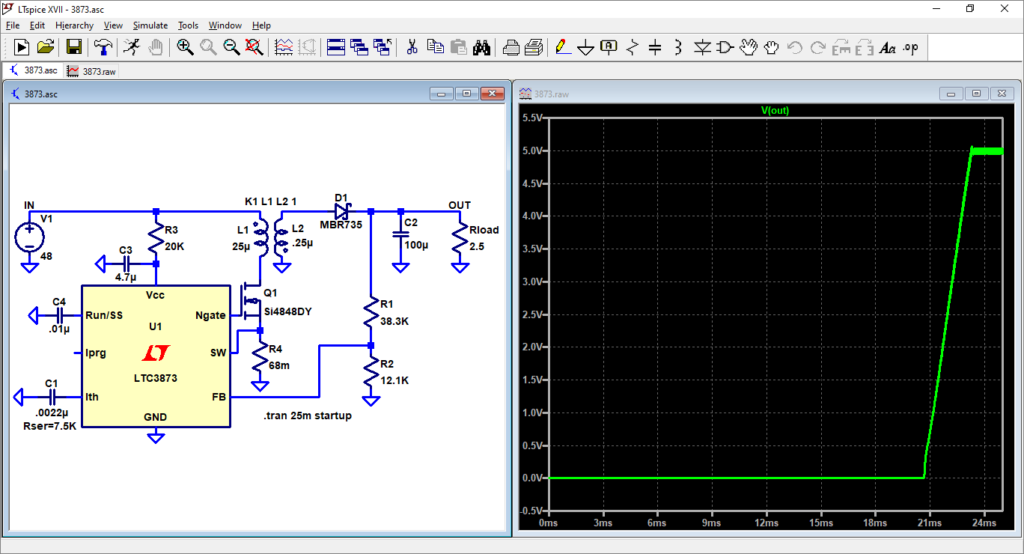Gambar 6. Simulasi flyback converter dengan IC LTC3873.
Komponen LTC3837 dapat diganti dengan LTC3837-5 untuk rangkaian yang hampir identik. Tetapi perlu diperhatikan bahwa susunan pin di model simulasi untuk kedua komponen tidak sama, seperti terlihat di Gambar 7.
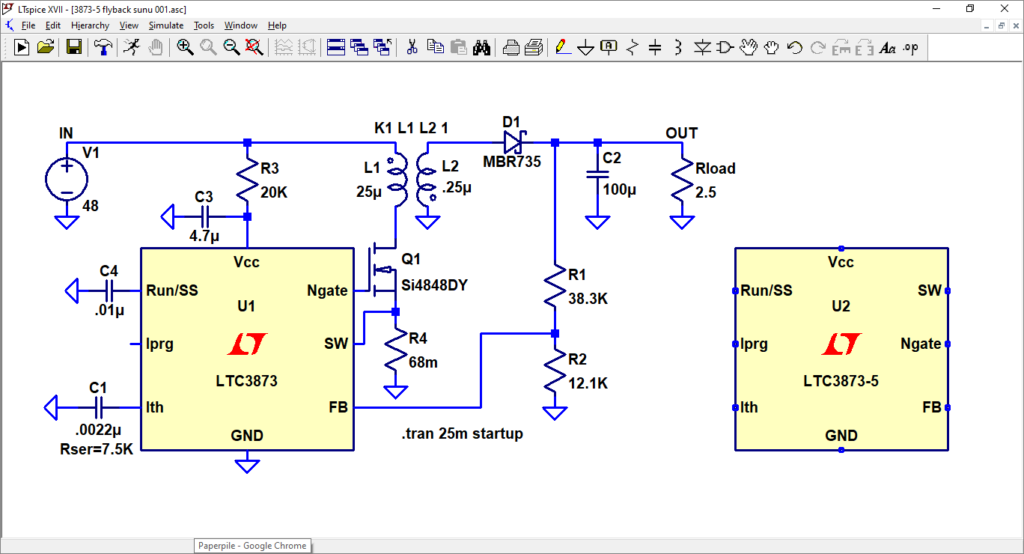Gambar 7. Model komponen LTC3873 dan LTC3873-5.
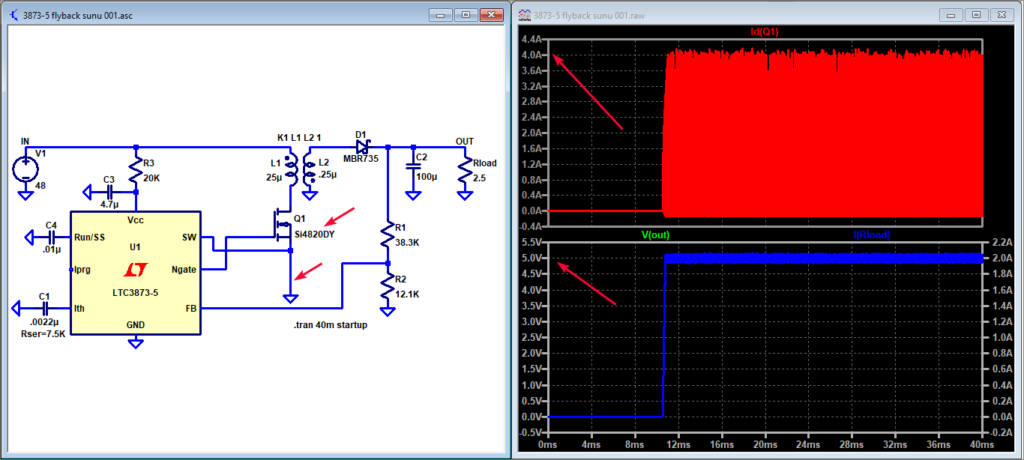Gambar 8. Pergantian komponen IC regulator.
Gambar 8 memperlihatkan bagaimana saya mengganti komponen LTC3873 dengan LTC3873-5. Kemudian yang ditunjukkan dengan panah merah di rangkaian adalah posisi RSENSE (untuk current sense) yang saya hilangkan. Begitu juga MOSFET telah diganti dengan yang lebih mampu mengalirkan arus yang lebih besar, bandingkan dengan rangkaian di Gambar 7. Cara ini adalah cara quick-and-dirty, sekadar untuk membuktikan bahwa IC LTC3837-5 itu dapat dipergunakan sebagai pengganti di rangkaian flyback converter itu. Untuk penerapan yang lebih baik, silakan membaca dengan lebih seksama datasheet. Cara ini saya tempuh karena sudah ada contoh yang lebih baik dan lebih lengkap yang bisa ditemukan di Internet, lihat Gambar 9.
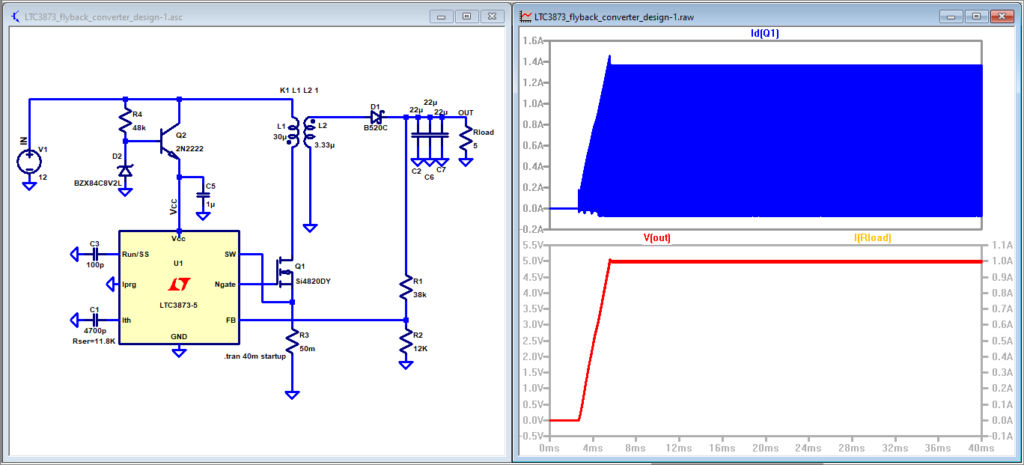Gambar 9. Contoh penerapan LTC3837-5 dalam simulasi [sumber].
Gambar 9 adalah screenshot dari simulasi yang dirancang oleh Simon Bramble. Modifikasi di Gambar 8 pun sebenarnya terinspirasi dari artikel Flyback Converter Design (oleh Simon Bramble). Di sana telah disajikan dengan sangat baik mengenai salah satu komponen IC regulator yang dipakai di sebuah sistem flyback converter. Silakan membaca langsung di website penulisnya.
Sebagai catatan penting, rancangan ini adalah contoh nonisolated flyback converter (Simon Bramble menyebutnya sebagai pseudo-isolated). Mengapa demikian? Karena kalau diperhatikan dengan baik, sisi primer dan sisi sekunder tidak benar-benar terpisah secara absolut. Ada R1 dan R2 yang berfungsi sebagai sensor pembagi tegangan yang ‘menghubungkan’ sisi sekunder ke primer, meskipun ‘hanya’ terhubung ke komponen IC regulator. Di beberapa desain lain, cara ini digantikan dengan menggunakan optocoupler. Ada juga rancangan yang melakukan pengendalian hanya dari sisi primer, menggunakan gejala di flyback transformer sebagai (umpan balik) penanda kondisi di sisi sekunder.
Setelah contoh dari Analog Devices (Linear Technology) dengan simulasi di LTspice, di bagian ini akan dipaparkan contoh kalkulasi/simulasi dengan PSD. Dimulai dengan rancangan yang secara default akan muncul saat topologi flyback converter dipilih. Nilai parameter rancangan yang dipergunakan berasal dari dokumen PMP4626 RevE – test report (Industrial Flyback with TPS40210 and universal transformer).
Di sini tidak akan dipelajari perancangan lengkap untuk sistem, meteri itu di luar jangkauan peruntukan materi belajar. Tetapi bukan berarti mahasiswa tidak bisa mempelajari bagaimana suatu power stage dari flyback converter dirancang. Pilihan lingkup materi belajar ini juga bisa dipakai untuk ‘menyambungkan cerita’ agar pelajaran yang sedang ditekuni memiliki konteks ke penggunaan yang lebih nyata di dunia luar kampus.
Gambar 10. Document header.
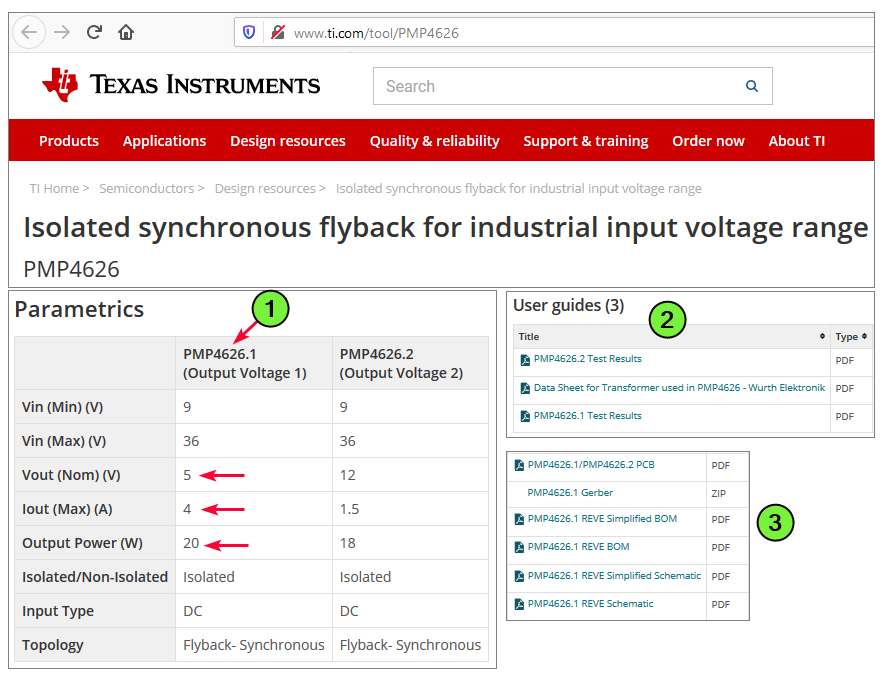Gambar 11. PMP4626 web page.
File pdf di Gambar 10 didapat di halaman web di Gambar 11. Penanda 1 menunjukkan bahwa design reference yang hendak dipakai adalah PMP4626.1, jangan sampai salah memilih. Di Penanda 2 diperlihatan dokumen-dokumen utama yang bisa diunduh untuk dipelajari. Di Penanda 3, adalah file-file rancangan yang sesuai untuk mempelajari perhitungan/simulasi atau bahkan untuk membuatnya dalam bentuk konverter fisik.
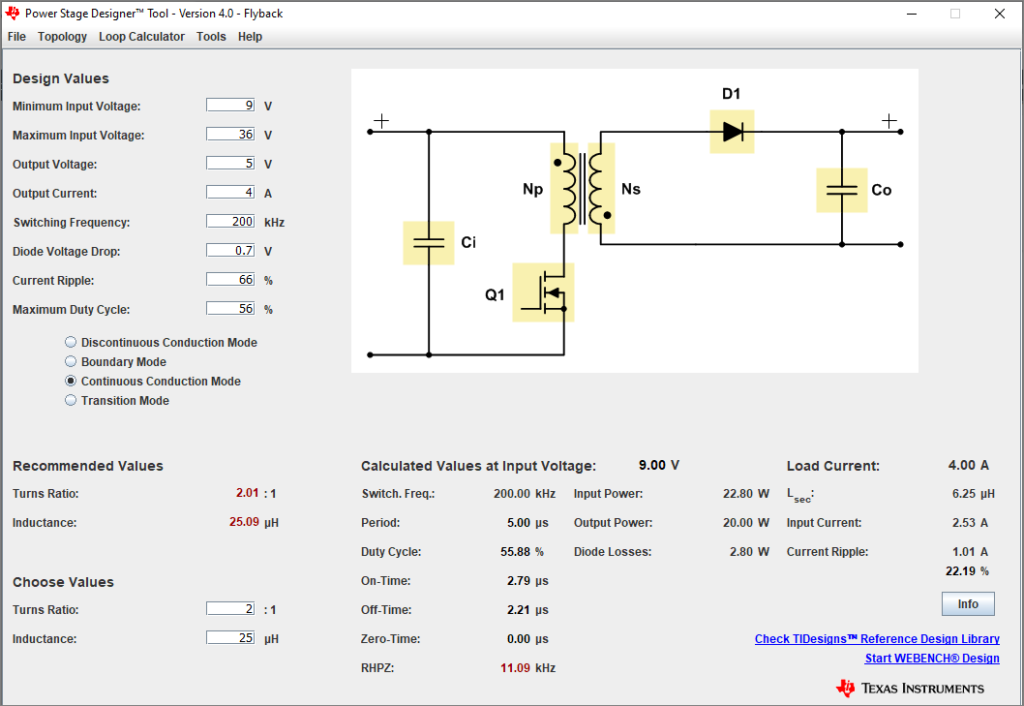Gambar 12. Perancangan awal secara default.
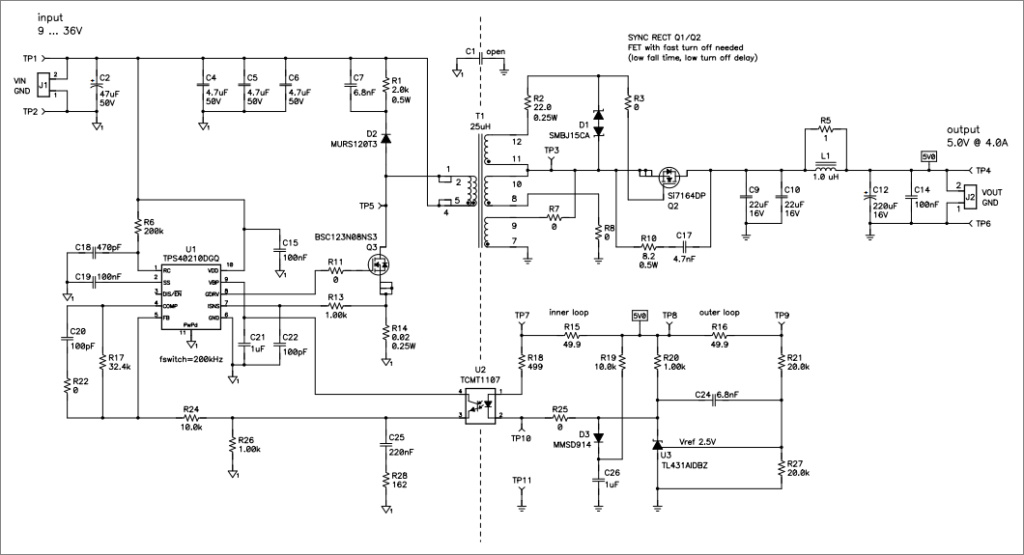Gambar 13. Skema, slur281 PMP4626.1 REVE Simplified Schematic.
Dari Gambar 13, bisa dilihat bahwa power stage dari sebuah konverter seperti flyback converter ‘hanyalah’ salah satu bagian (penting). Ada bagian-bagian lain yang diperlukan agar suatu closed-loop flyback converter dapat bekerja sesuai sasaran rancangan. Misalnya komponen optocoupler yang diberi penanda komponen U2. Keberadaan komponen inilah yang membuat suatu flyback converter menjadi konverter yang benar-benar memiliki isolasi antara sisi primer dan sisi sekunder trafo.
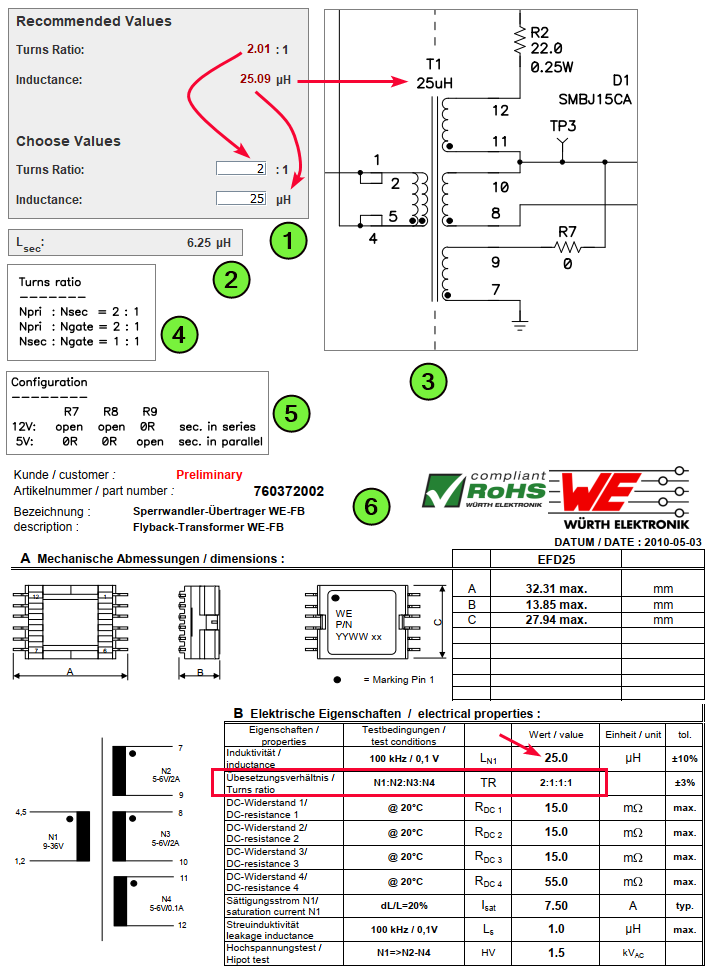Gambar 14. Flyback transformer.
Di Gambar 14, Penanda 1 dan Penanda 2 adalah screenshot dari rancangan awal PSD. Penanda 3, Penanda 4, dan Penanda 5 adalah gambar dari skema rancangan rangkaian. Penanda 6 adalah screenshot dari datasheet jenis trafo yang direncanakan akan dipergunakan. Jika diperlukan untuk mengingat kembali hubungan nilai induktansi dan rasio gulungan (juga tegangan dan arus), silakan lihat artikel sebelumnya (link).
Sebagaimana yang sering diungkap di beberapa application note, pemilihan flyback transformer bukanlah hal yang gampang. Berbagai aspek perlu diperhitungkan agar sasaran perancangan sistem tercapai. Tidak jarang satu parameter/faktor akan bertentangan dengan faktor lain sehubungan dengan ketersediaan komponen. Tidak semua designer memiliki kemewahan untuk dapat menggunakan trafo yang khusus dibuat untuk rancangannya (custom). Kecuali ada justifikasi ekonomi dan memiliki pembenaran yang kuat. Untungnya dengan dipergunakannya IC regulator komersial, penggunaan trafo yang tidak persis sesuai rancangan masih bisa diakomodasi. Misalnya tentang penentuan nilai tegangan keluaran, di beberapa IC nilai ini ditentukan dengan rasio resistor pembagi tegangan yang berfungsi sebagai sensor bagi regulator. Ada juga yang menggunakan umpan balik yang di dalamnya terdapat isolasi optik seperti di Gambar 13. Sehingga tidak lagi murni bergantung pada nilai rasio gulungan primer dan sekunder dari flyback transformer.
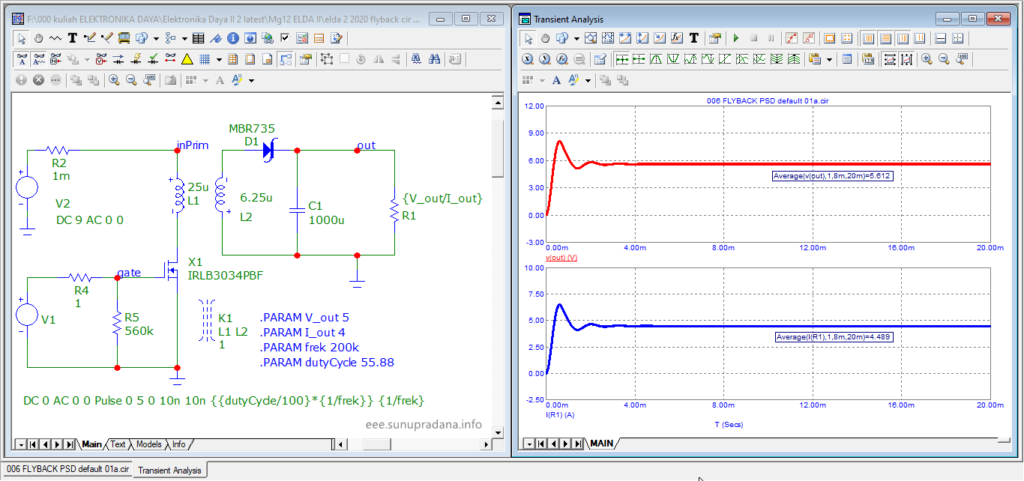Gambar 15. Simulasi flyback converter power stage.
Simulasi di Gambar 15 adalah simulasi perwujudan dari perhitungan / simulasi di Gambar 12. Tegangan yang dipakai untuk simulasi adalah tegangan minimum, yaitu 9 V.
Di bagian berikut ini masih merupakan sambungan di bagian sebelumnya untuk rancangan yang sama. Sebelum melakukan simulasi baru dengan simulator SPICE, kita akan melihat contoh bagian dari dokumen pengujian (alat yang sudah diwujudkan secara fisik) yang dilakukan oleh engineer di perusahaan Texas Instruments.
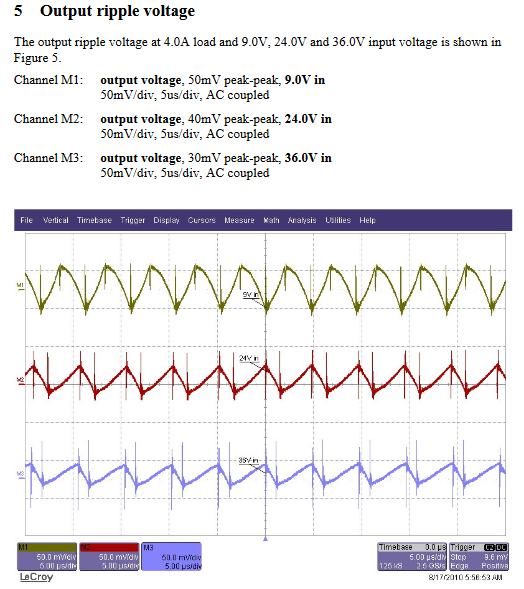Gambar 16. Pengujian riak tegangan keluaran.
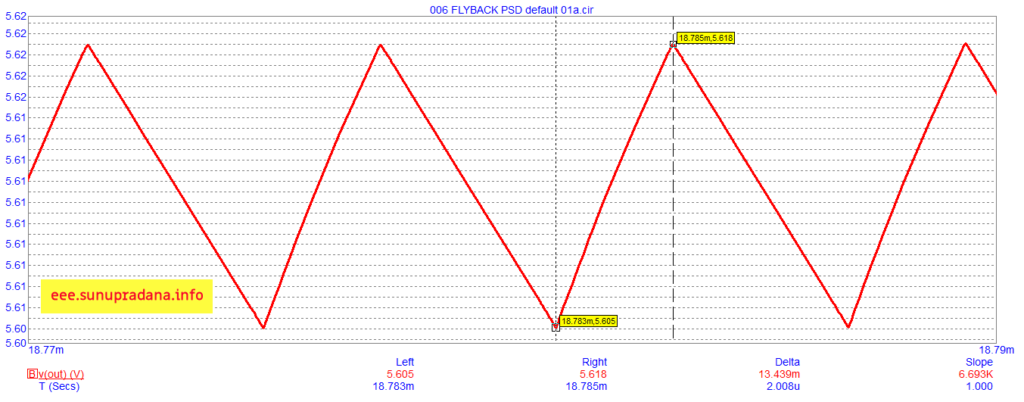Gambar 17. Simulasi Vout dengan Vin=9 V dan Iout=4 A.
Kurva di Gambar 17 adalah hasil zoom-in simulasi dari Gambar 15. Perlu diketahui bahwa sampai saat ini sulit diharapkan bahwa dc-dc converter komersial (sekalipun) yang merupakan SMPS dapat memberikan tegangan dan arus yang benar-benar rata seperti layaknya sebuah cell/battery baru dengan beban proporsional. Melalui proses belajar dengan melihat dan membaca dokumen pengujian sistem fisik seperti di Gambar 16, kita bisa memperoleh keyakinan terhadap pola dasar yang diberikan oleh simulator seperti di Gambar 17. Riak tegangan/arus di output itu selalu ada, hanya saja nilainya yang bisa diusahakan semakin rendah.
Untuk keterangan lebih lengkap mengenai salah satu contoh bagaimana sebuah laporan pengujian sistem power management dilakukan, silakan membaca dokuman aslinya di link ini. Misalnya, di dokumen itu diperlihatkan bagaimana suatu sistem catu daya saat startup dan shutdown. Tidak ada overshoot tegangan seperti yang ditemui di sistem open-loop (hanya terdiri dari power stage), lihatlah kembali Gambar 15.
Di bagian ini akan dilakukan penyederhanaan rancangan PSD di Gambar 12 dengan hanya menggunakan satu nilai input, yaitu 9 V.
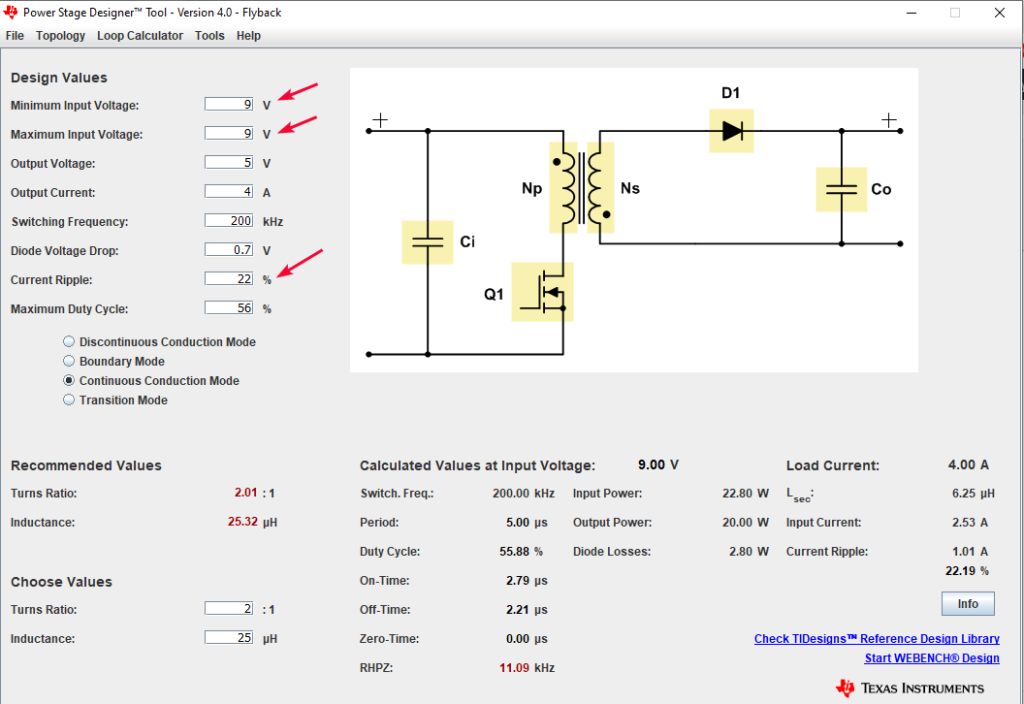Gambar 18. Desain dasar flyback converter power stage.
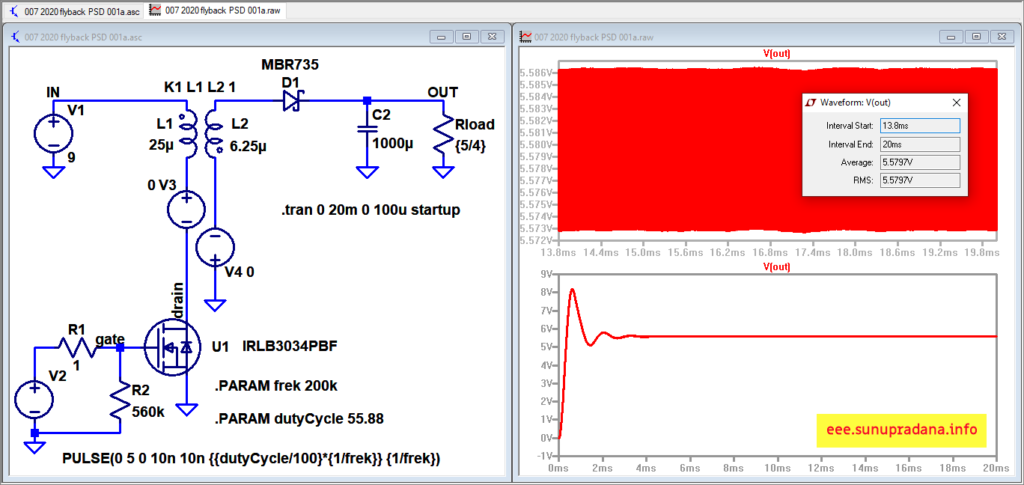Gambar 19. Simulasi dengan LTspice.
Di LTspice terdapat fasilitas yang memungkinkan satu gelombang dapat ditampilkan lebih dari satu kali di pane yang berbeda. Kemudian jika Sync. Horiz. Axes dinonaktifkan, maka seperti di Gambar 19 masing-masing pane bisa diatur untuk memiliki rentang sumbu horizontal yang berbeda. Bagian atas adalah bagian saat dilakukan zoom-in terhadap batas sumbu-X yang menandai waktu.
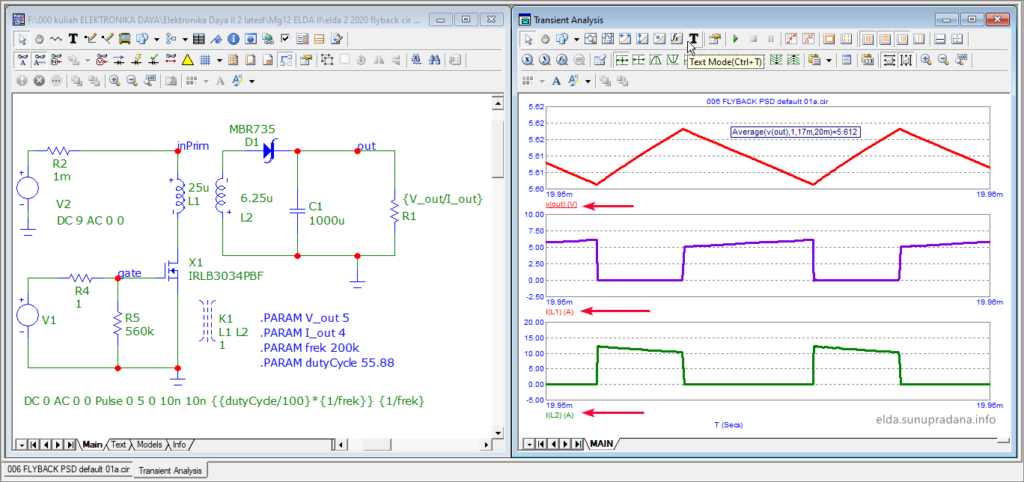Gambar 20. Simulasi dengan MC-12.
Dengan simulasi, meski masih tanpa perhitungan, sudah bisa dilihat adanya risiko di rangkaian. Misalnya, di Gambar 20 ada risiko arus IL2 akan mendekati 15 A. Padahal rating IFRM untuk diode Schottky MBR735 adalah 7.5 A. Untuk itu akan dicoba menggunakan model diode Schottky yang lain (yang juga telah tersedia di simulator tetapi) dengan rating arus yang lebih tinggi, MBRB2545CT dari Onsemi.
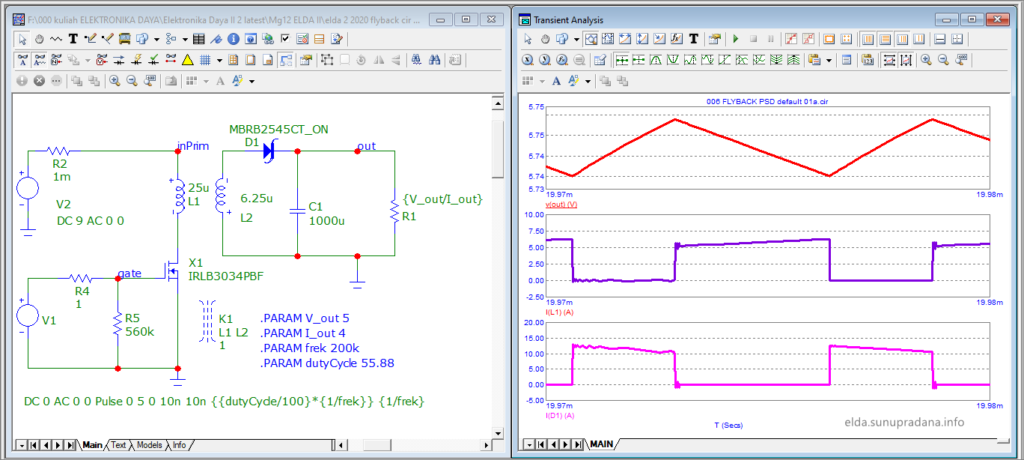Gambar 21. Simulasi dengan MC-12 (w/MBRB2545CT_ON).
Penggantian diode tidak banyak mengubah hasil simulasi, terlihat di Gambar 21. Kasus simulasi dengan diode ini menjadi salah satu contoh bahwa simulasi selalu perlu dilakukan dengan hati-hati. Simulator tidak selalu memberi peringatan tentang potensi bahaya. Pengguna dan designer wajib untuk selalu menggunakan pengetahuan dan akal sehat terutama saat simulasi dilakukan pada tahapan menjelang pembuatan prototipe. Di saat inilah komponen-komponen yang akan dibeli ditetapkan. Perubahan komponen tidak hanya akan mengubah BOM (Bill of Materials), tetapi juga berisiko mengubah rancangan jalur PCB. Sebab bukan tidak mungkin pengubahan komponen juga disertai dengan perubahan bentuk fisik komponen. Itulah sebabnya datasheet harus selalu dijadikan salah satu bahan acuan.
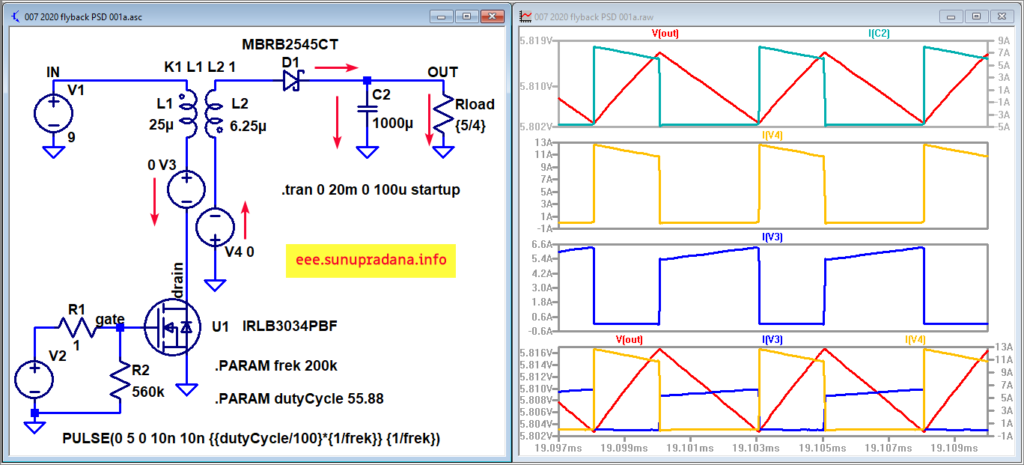Gambar 22. Simulasi dengan LTspice (w/MBRB2545CT_ON).
Di Gambar 22 dapat dilihat adanya sumber tegangan V3 dan V4, keduanya bernilai 0 volt. Bagi ‘generasi lama’ yang sudah terbiasa dengan era MicroSim PSpice akan segera teringat akan kegunaannya. Kedua sumber tegangan itu hanya dummy/bogus, tidak memberikan kontribusi apa pun untuk tegangan di rangkaian. Fungsinya adalah sebagai instrumen pengukuran arus di node di mana ia ditempatkan. Cara ini sepertinya sudah jarang dipakai, karena ada cara-cara lain yang lebih mudah atau lebih kecil kemungkinannya untuk membingungkan pengguna.
Di LTspice model komponen L, C, dan bahkan R seolah-olah memiliki polaritas. Hal ini tentu tidak nyata secara fisik, tetapi cara ini diperlukan untuk menentukan referensi arah. Masih ingat dengan passive sign convention? Jika arah bersesuaian maka nilainya positif, jika berlawanan maka nilainya akan ditandai negatif meskipun nilai absolutnya sendiri tidak berubah. Maka setiap komponen L seperti di Gambar 22 memiliki arah referensi arus yang sudah ditetapkan. Karena itu jika hendak mengambil referensi arah sebaliknya, variabel dikalikan dengan -1. Misalnya untuk arus di L2, arah referensi arus yang ditetapkan oleh LTspice adalah keluar dari tanda titik (dot), di Gambar 22 ke arah bawah. Maka jika hendak menetapkan arah arus ke atas sebagai arah arus positif, pengukuran harus dilakukan dengan menggunakan -I(L2) dan bukan I(L2). Nilai arus sebenarnya sama saja, hanya tandanya saja yang diubah.
Cara di paragraf di atas sebenarnya tidak ada masalah untuk dipergunakan. Saya hanya menunjukkan cara di Gambar 22 terutama bagi mahasiswa sebagai wawasan dan menunjukkan pengaturan yang khas dari LTspice (keluarga SPICE).
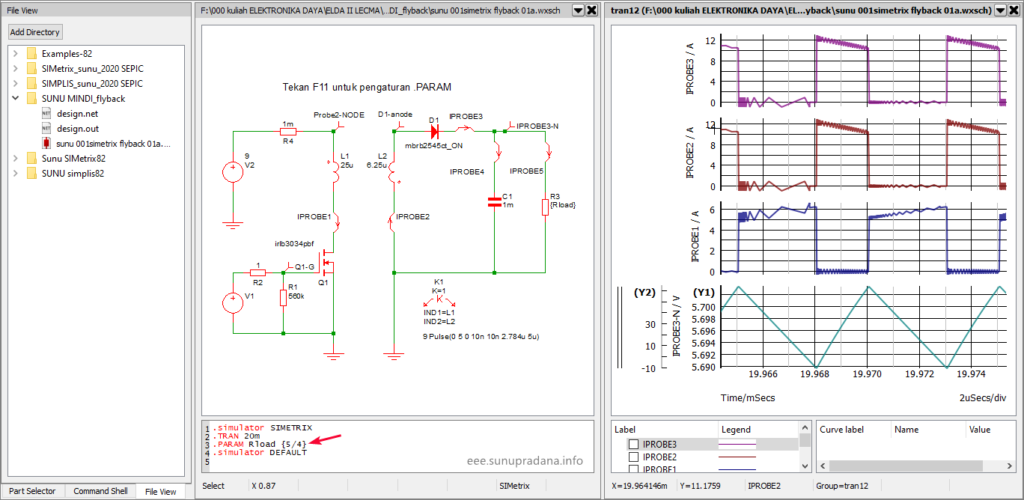Gambar 23. Simulasi dengan SIMetrix (w/MBRB2545CT_ON).
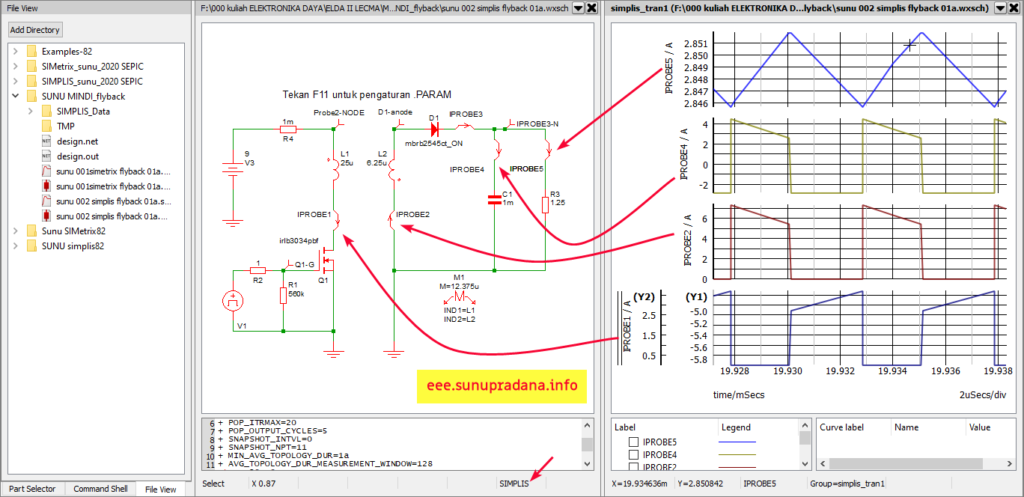Gambar 24. Simulasi dengan SIMPLIS (w/MBRB2545CT_ON).
Penandaan coupling untuk induktor di Gambar 24 (SIMPLIS) berbeda cara dengan yang di Gambar 23 (SIMetrix). Persamaan untuk mengisi nilai mutual inductor di SIMPLIS dapat dilihat di link ini.
Sebagai catatan, semua simulasi dengan simulator yang berbeda-beda di atas menghasilkan nilai tegangan keluaran yang berbeda dengan yang dihasilkan oleh PSD. Ini karena model komponen SPICE yang dipergunakan jelas berbeda dengan model ideal, belum lagi kemungkinan engine silmulasi diatur dengan parameter yang berbeda pula. Maka nilai duty cycle harus disesuaikan ulang agar simulasi bisa menghasilkan nilai tegangan keluaran yang sesuai rancangan. Bahkan jika power stage ini diwujudkan menjadi suatu open-loop flyback converter secara fisik, maka nilai duty cycle pun akan perlu diubah kembali. Jika menggunakan IC regulator, maka pengaturan duty cycle akan diatur secara otomatis oleh regulator.
Setelah mencoba melakukan simulasi untuk mendapatkan gambaran umum operasi sistem rangkaian yang sedang dirancang, berikut ini akan dilakukan perhitungan manual sebagai pembanding dari nilai yang dihasilkan oleh PSD. Persamaan-persamaan dan perhitungan yang akan dilakukan di sini akan mengacu ke artikel sebelumnya. Simulasi LTspice juga diubah untuk dapat mendekati kondisi simulasi PSD, lihat Gambar 25.
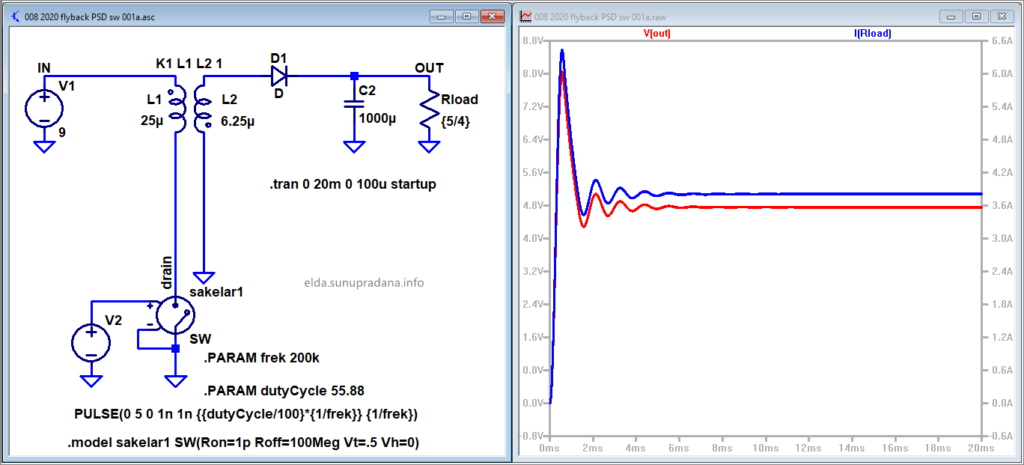Gambar 25. Simulasi LTspice dengan model komponen mendekati ideal.
Gambar 26 berikut adalah kutipan dari parameter-parameter desain di Gambar 18 yang diatur ulang untuk memudahkan pembacaan. Nilai tegangan input hanya dipakai satu, tidak menggunakan rentang nilai. Ini untuk memudahkan contoh/pembuktian perhitungan saja. Begitu sudah familiar dengan versi satu nilai, bisa dicoba untuk penggunaan dengan rentang nilai masukan.
Penanda 1 menunjukkan nilai-nilai variabel yang dimasukkan oleh pengguna sebagai bahan perhitungan oleh PSD. Nilai ini adalah nilai yang ditetapkan atau ingin dicapai sebagai hasil dari perancangan. Nilai maximum duty cycle di rancangan aslinya memang sebesar 56%, umumnya untuk flyback converter disarankan untuk mencoba mencapai batas maksimum di bawah 50%. Kemungkinan nilai ini dinaikkan menjadi 56% agar rekomendasi untuk Turns Ratio dapat mendekati 2 dibanding 1. Berikutnya dari pilihan empat mode operasi, perancang memilih untuk menggunakan mode CCM.
Penanda 2 menunjukkan nilai yang direkomendasikan oleh PSD untuk dipakai. Nilai ini didapat sebagai hasil perhitungan dari parameter yang dimasukkan oleh pengguna (perancang) di bagian Penanda 1. Nilai ini tidak selalu harus dipatuhi, apalagi dianggap mutlak persis sama. Tetapi semakin dekat nilai yang dipakai dengan nilai rekomendasi ini maka akan semakin dekat nilai parameter operasi dengan nilai yang diinginkan untuk dicapai.
Salah satu penyebab mengapa nilai-nilai rekomendasi tidak selalu dapat diikuti adalah karena kenyataan ketersediaan komponen. Ini adalah kenyataan yang harus dikompromikan. Kadang-kadang seorang desainer memang memiliki ‘kemewahan’ untuk dapat menentukan apa saja komponen yang akan dipakai. Meskipun untuk itu sering kali harus menggunakan komponen yang dipesan khusus (custom). Terutama kalau rancangan memiliki nilai strategis yang sangat tinggi dari berbagai aspek. Tetapi yang jauh lebuh sering terjadi di kehidupan nyata adalah bahwa perancang lah yang harus menyesuaikan rancanganannya dengan komponen yang lebih mudah didapat (dan lebih murah). Untuk itu, proses desain sering sekali bukanlah suatu proses yang ‘sekali jalan’ atau ‘sekali jadi’. Bukan seperti waterfall, tetapi suatu proses iteratif yang berulang-kali secara cyclic. Untuk bagian trial-and-error, proses coba-cobanya kadang-kadang bahkan dilakukan dengan melompat-lompat.
Penanda 3 menunjukkan nilai yang dipilih oleh perancang. Lagi, nilai ini didapat dari kompromi berbagai aspek perancangan dan produksi.
Penanda 4 dan Penanda 5 merupakan hasil perhitungan sebagai respon dari masukan di bagian Penanda 1 dan Penanda 3. Nilai ini tentu dapat berubah / diatur ulang jika pengguna mengubah nilai yang diisi. Di sini dapat dilihat bahwa dalam bentuk perhitungan ini pun nilai Diode Losses: 2.80 W. Karena itu sering dikatakan bahwa disipasi daya terbesar untuk flyback converter power stage ada pada diode.
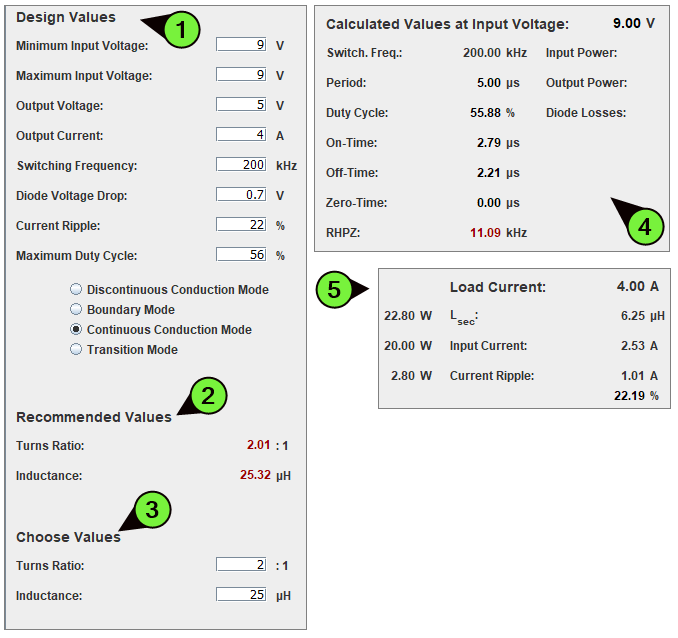Gambar 26. Kutipan parameter dari rancangan di PSD.
Perhitungan (1): Nilai duty cycle, alternatif 1
Nilai duty cycle bisa diperoleh dari beberapa cara, antara lain dengan modifikasi persamaan. Tetapi mari mulai dengan cara yang lebih sederhana, lihat persamaan di Gambar 16 di artikel ini. Kita mulai perhitungan dari sudut pandang pemeriksaan rancangan rangkaian.
\(\LARGE D_{CCM}=\frac{V_o}{n_2 \times V_i + V_o}\)Yang bisa dimodifikasi untuk memasukkan nilai jatuh tegangan diode sebesar 0.7 V, bisa dibandingkan dengan perhitungan (4) di Gambar 10 di artikel ini. Sehingga persamaan menjadi seperti berikut:
\(\LARGE D_{CCM}=\frac{V_o + V_D}{(n_2 \times V_i) + (V_o + V_D)}\)Sehigga didapat perhitungan:
\(\LARGE D_{CCM}=\frac{5 + 0.7}{(\frac{1}{2} \times 9) + (5 + 0.7)}\) \(\LARGE D_{CCM}=\frac{5.7}{10.2}\) \(\LARGE D_{CCM}= 0.55882353\)Hasil perhitungan ini sebanding dengan nilai D = 55.88% dari PSD.
Untuk memeriksa balik nilai perhitungan itu dapat dilakukan dengan cepat juga, Gambar 17 di artikel ini. Hasilnya, dengan nilai duty cycle sebesar itu jika nilai masukan sebesar 9 V maka keluaran akan didapat sebesar 5 V. Bisa dilihat di Gambar 26, hasil perhitungan ini sama dengan hasil simulasi PSD, yang juga sama dengan target rancangan rangkaian oleh perancangnya (Gambar 10 dan Gambar 11).
Perhitungan (2): Nilai tON dan tOFF, alternatif 1
Nilai periode dapat diperoleh dari nilai frekuensi penyakelaran yang ditetapkan:
\(\LARGE T=\frac{1}{f} = \frac{1}{200\textrm{E}3} = 5 \;\mu\)Jika nilai frekuensi adalah 200 kHz maka nilai periode adalah 5 μS. Jika nilai duty cycle diketahui maka nilai tON dapat dicari:
\(\LARGE D = \frac{t_{ON}}{T}\) \(\LARGE t_{ON} = {D}\times{T} = \frac{5.7}{10.2}\times\frac{1}{200\textrm{E}3}=2.79411765 \mu\)Maka diperoleh nilai tON sebesar 2.79 μS, yang sesuai dengan perhitungan PSD.
\(\LARGE t_{OFF} = T-({D}\times{T}) \) \(\LARGE t_{OFF} = 1-\left( \frac{5.7}{10.2}\times\frac{1}{200\textrm{E}3} \right)\) \(\LARGE t_{OFF} = 5 \mu -2.79411765 \mu = 2.20588235 \mu\)Maka diperoleh nilai tOFF sebesar 2.21 μS, sesuai dengan perhitungan PSD.
Perhitungan (3): Nilai duty cycle, alternatif 2
Di Perhitungan (1) terdapat variabel n2 yang merupakan rasio nilai gulungan sekunder terhadap nilai gulungan primer yang dinormalisasi (menjadi 1). Ini berarti nilai rasio harus diketahui atau ditetapkan terlebih dahulu. Bagaimana jika kita masih dalam tahap proses perancangan yang belum mengetahui nilai rasio dari flyback transformer?
Dengan bersedia belajar dari ‘pengalaman orang lain’ kita bisa temukan solusi cepatnya, ada di Gambar 10 artikel ini (link). Dokumen yang diacu adalah dokumen contoh tahapan proses desain, sehingga alur pikirnya berbeda dengan alur berpikir untuk proses penjelasan atau verifikasi / pemeriksaan / pembuktian rancangan.
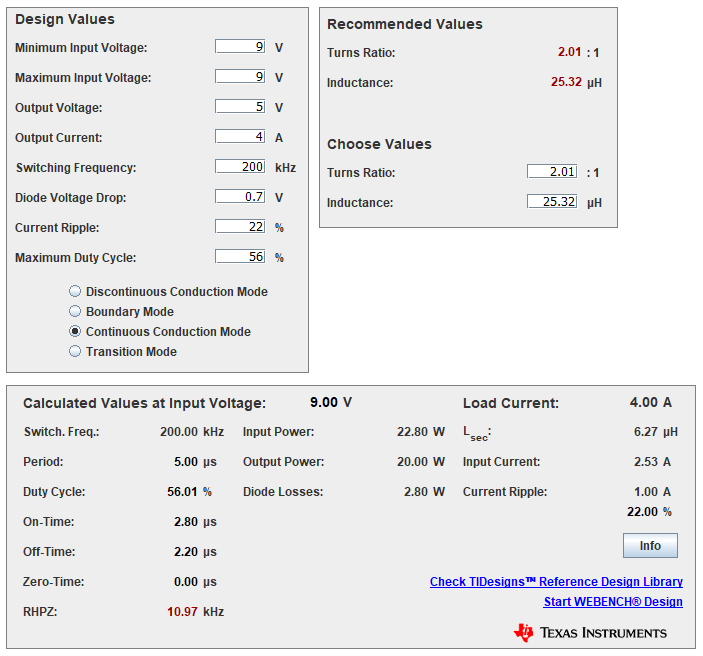Gambar 27. Simulasi PSD untuk perhitungan cara alternatif 2.
Perhatikan bahwa di Gambar 26 dan di Gambar 27, perancang telah memasukkan nilai parameter Maximum Duty Cycle sebesar 56%. Nilai ini adalah engineering judgement yang berasal dari datasheet, application note, maupun pengalaman / knowledge base dari sang perancang. Dalam kasus ini, kemungkinan perancang sudah melakukan penyesuaian ulang rancangan agar sesuai dengan trafo yang tersedia. Nilai 56% ini akan dipergunakan sebagai bahan perhitungan awal.
\(\LARGE \textrm{Np2s} = \frac{V_{IN} \times D_{limit}}{(V_{out}+V_D) \times (1-D_{limit})}\) \(\LARGE \textrm{Np2s} = \frac{9 \times 0.56}{(5+0.7) \times (1-0.56)} = 2.00956938\)Hasil perhitungan sesuai dengan rekomendasi rasio sisi primer terhadap sisi sekunder PSD, yaitu 2.01. Dari nilai ini yang kemudian oleh perancangnya diambil pembulatan 2:1 sebagaimana di Gambar 26.
Selanjutnya masih dengan menggunakan contoh di Gambar 10 artikel ini (link), bisa dicari nilai D yang direkomendasikan seandainya menggunakan rasio 2.01:1 untuk flyback transformer. Persamaan berikut ini sebenarnya adalah penyusunan ulang dari persamaan sebelumnya. Dalam praktik perancangan, dipakai untuk menentukan nilai D jika nilai rasio gulungan trafo yang akan dipakai tidak sama hasil perhitungan sebelumnya. Tetapi kali ini dipakai hanya sebagai konfirmasi simulasi.
\(\LARGE D_{CCM} = \frac{(V_{out}+V_D) \times \textrm{Np2s}}{V_{IN}+((V_{out}+V_D) \times \textrm{Np2s})}\) \(\LARGE D_{CCM} = \frac{(5+0.7) \times 2.01}{9+((5+0.7) \times 2.01)} = 0.56005279\)Maka nilai duty cycle yang dihitung oleh PSD adalah 56.01 % jika menggunakan rasio 2.01:1 untuk flyback transformer. Nilai perhitungan balik ini melebihi 56% karena adanya pembulatan.
Perhitungan (4): Nilai tON dan tOFF, alternatif 2
Dengan menggunakan nilai duty cycle 56.01% (sebagai akibat dari penggunaan rasio 2.01:1) maka dapat dicari waktu ON sakelar:
\(\LARGE t_{ON} = {D}\times{T} = 0.5601 \times\frac{1}{200\textrm{E}3}=2.80 \,\mu\) \(\LARGE t_{OFF} = T-({D}\times{T})= 5 \,\mu-({0.5601}\times{5 \,\mu}) = 2.1995 \,\mu \approx 2.20 \,\mu\)Waktu ON=2.80 μS. Waktu OFF=2.20 μS, sesuai dengan hasil simulasi di Gambar 27.
Perhitungan (5): Induktansi sisi primer transformer (konfigurasi alternatif 2)
Di artikel di link ini telah disampaikan mengenai magnetizing inductance dan peran pentingnya untuk sistem flyback converter. Di saat diode di sisi sekunder off maka aliran arus dari sumber tegangan di sisi primer mengalir melalui magnetizing inductance ini sebagai induktor tunggal (virtual). Energi disimpan sementara waktu sampai dapat disalurkan ke beban di saat sakelar (MOSFET) off.
Masih dengan menggunakan alur pikir desain (alternatif 2), dicari beberapa parameter penting dari operasi power stage dari flyback converter.
Nilai riak arus induktor dapat dicari dengan:
\(\LARGE I_{RIPPLE}=\textrm{RIP%} \times \frac{V_{OUT} \times I_{OUT}}{V_{IN}\,max \times D_{min}}\) \(\LARGE I_{RIPPLE}=\textrm{RIP%} \times \frac{(V_{OUT}\,+\,V_D) \times I_{OUT}}{V_{IN}\,max \times Dmin}\) \(\LARGE I_{RIPPLE}= 0.22 \times \frac{(5+0.7) \times 4}{9 \times 0.5061} = 0.9950604\)Riak arus, IRIPPLE, sebesar 0.995 A ≈ 1 A. Nilai ini bersesuaian dengan perhitungan PSD yang menunjukkan selisih 0.99 A atau tampilan ripple 1 A.
Nilai induktansi sisi primer trafo yang juga menjadi nilai induktor sisi primer (magnetizing inductance, LM) dapat dihitung:
\(\LARGE L_{PRI} = \frac {V_{IN}\,max \times Dmin}{I_{RIPPLE} \times f_{SW}}\) \(\LARGE L_{PRI} = \frac {9 \times 0.5061}{0.9950604 \times 200\textrm{E}3} = 25.32961818 \approx 25.32\,\mu\)Maka nilai rekomendasi untuk LPRIM = LM = Lm ≈ 25.32 μH, ini sama dengan hasil simulasi dari PSD.
Perhitungan (6): Perhitungan komponen sakelar (konfigurasi alternatif 2)
Suatu catu daya tersakelar dapat disimulasikan dengan sakelar ideal, tetapi tetap harus diwujudkan dengan komponen fisik yang tidak ideal. Misalnya dengan komponen diskrit BJT, MOSFET, atau IGBT. Bisa juga dengan komponen transistor yang sudah terintegrasi ke dalam IC regulator (internal switching). Kita dapat mengantisipasi kisaran batasan kemampuan minimal yang perlu dimiliki oleh transistor untuk dapat menjalankan fungsinya sebagai sakelar agar rangkaian yang dirancang berhasil mencapai target.
Pertama, suatu sakelar perlu memiliki kemampuan untuk bekerja dengan level tegangan maksimal tertentu di antara kaki-kakinya, termasuk saat overshoot. Jika kemampuan sakelar lebih rendah dari tegangan yang mungkin muncul, maka sakelar akan rentan rusak. Misalnya, sebuah MOSFET harus memiliki rating drain-source voltage yang mencukupi, sesuai dengan kebutuhan desain (lebih baik di atas batas dengan margin pengaman).
\(\LARGE V_{FET} = \frac {V_{IN}\,max + ((V_{OUT}+V_D)\times \textrm{Np2s})}{\textrm{inverse margin value}}\)Nilai margin yang disarankan misalnya adalah 20%, maka nilai pembagi menjadi 0.8, sebaliknya untuk perhitungan ideal 100% maka nilai yang dipakai sebagai pembagi adalah 1.
\(\LARGE V_{FET} = \frac {9 + ((5+0.7)\times 2.01)}{1} = 20.457 \approx 20.46\)Dapat dilihat di Gambar 28 bahwa hasil perhitungan manual bersesuaian dengan hasil simulasi PSD.
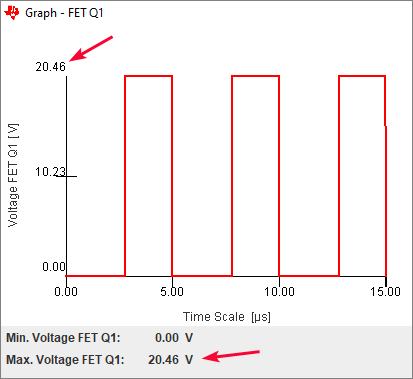Gambar 28. Simulasi nilai tegangan antara drain-source di MOSFET.
Namun disarankan agar perhitungan memberi margin, karena terdapat beberapa kondisi yang tidak ideal saat perwujudan prototipe nantinya. Misalnya ada leakage inductance atau ringing yang disebabkan oleh unsur parasitic termasuk dari jalur di PCB. Berikut ini contoh perhitungan jika memasukkan margin sebesar 20%.
\(\LARGE V_{FET} = \frac {9 + ((5+0.7)\times 2.01)}{0.8} = 25.57125\)Nilai baru dari perhitungan sepadan dengan 25.57 V. Cara yang lebih mudah jika kita sudah memiliki baseline adalah dengan menghitung langsung dari kondisi ideal sebagai baseline.
\(\LARGE V_{FET} = \frac {20.46}{\frac{80}{100}} = 25.575\)Dengan asumsi margin 20% sudah cukup, maka perancang bisa mencari sakelar yang mampu menangani beda potensial sebesar 25.57 Volt. Jika masih ada ruang dari sisi ekonomi, nilai ini masih bisa ditingkatkan lagi untuk menambah faktor keamanan (meskipun harganya bisa jadi lebih mahal). Bandingkan hasil perhitungan dengan simulasi di Gambar 29 berikut ini, di bagian berikutnya nanti saya tampilkan yang sudah menggunakan model komponen MOSFET.
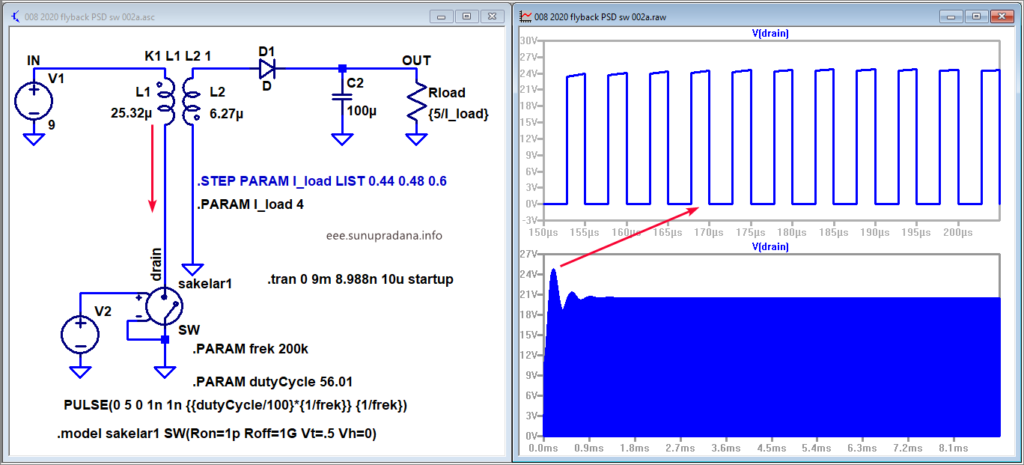Gambar 29. Simulasi tegangan di kaki-kaki sakelar.
Untuk contoh di simulasi di Gambar 29, seandainya nilai ini ingin diantisipasi maka margin dinaikkan dari 20% ke 30%, sehingga:
\(\LARGE V_{FET} = \frac {20.46 \,\textrm{V}}{\frac{70}{100}} = 29.23 \,\textrm{V}\)Komponen MOSFET dengan kemampuan VDSS (drain-source voltage) 40 V bisa diharapkan untuk menangani level tegangan ini. Dengan catatan bisanya parameter di datasheet diukur dalam kondisi operasi 25 °C.
Yang kedua, sebagai berikut adalah perhitungan nilai arus yang harus mampu ditangani oleh sakelar. Persamaan yang dipakai adalah persamaan yang dimodifikasi dari persamaan untuk mencari nilai IOUTmax yang dikutip di artikel ini.
\(\LARGE I_{OUT}\,max = \left( I_{LIM}\,min – \frac{I_{RIPPLE}}{2} \right) \times \frac{V_{IN}\,min\times D\,max \times \eta _{EST}}{V_{OUT}}\)Sebagai contoh, persamaan di atas dapat disusun ulang dengan berbagai cara. Salah satu cara adalah dengan menggunakan penyusunan per blok. Perubahan pertama adalah sebagai berikut:
\(\LARGE \frac {I_{OUT}\,max }{ \left( \frac{ V_{IN}\,min\times D\,max \times \eta _{EST}}{V_{OUT}} \right) } = \left( I_{LIM}\,min – \frac{I_{RIPPLE}}{2} \right)\)Perubahan kedua:
\(\LARGE \frac {I_{OUT}\,max }{ \left( \frac{ V_{IN}\,min\times D\,max \times \eta _{EST}}{V_{OUT}} \right) } + \frac{I_{RIPPLE}}{2} = I_{LIM}\,min\)Perubahan ketiga:
\(\LARGE I_{LIM}\,min = \left( I_{OUT}\,max \times \frac {V_{OUT}} {V_{IN}\,min\times D\,max \times \eta _{EST}} \right) + \frac{I_{RIPPLE}}{2}\)Perubahan terakhir untuk mengakomodasi VD:
\(\LARGE I_{LIM}\,min = \left( I_{OUT}\,max \times \frac {V_{OUT} + V_D} {V_{IN}\,min\times D\,max \times \eta _{EST}} \right) + \frac{I_{RIPPLE}}{2}\)Perhitungan dengan VD:
\(\LARGE I_{LIM}\,min = \left( 4 \times \frac {5 + 0.7} {9 \times 0.5601 \times 1} \right)+ \frac{0.9950604}{2}\) \(\LARGE I_{LIM}\,min = 4.52300184 + 0.4975302 = 5.02053204\)Berdasarkan perhitungan di atas, sakelar yang akan dipakai harus mampu menangani arus setidaknya sebesar 5.02 A.
Gambar 30. Simulasi arus di MOSFET menggunakan PSD.
Hasil perhitungan manual (dengan efisiensi 100%) di atas cocok dengan simulasi PSD yang menggunakan model ideal. Tetapi perhatikan Gambar 31 berikut ini. Lebih sering daripada tidak, nilai efisiensi ηEST tidak cocok diisi 100%, umumnya diisi setidaknya dengan 80%.
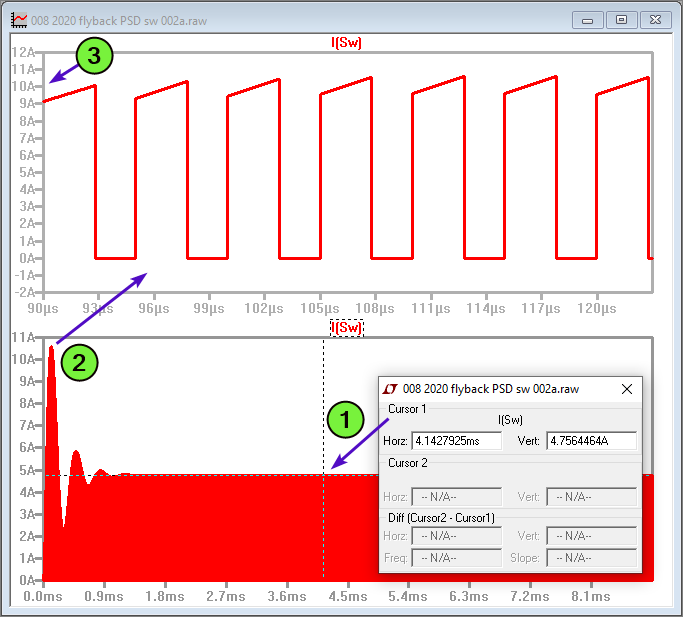Gambar 31. Simulasi arus MOSFET di flyback converter power stage.
Gambar 31 adalah hasil simulasi arus penyakelaran di model sakelar ideal dengan rangkaian yang sama seperti di Gambar 29. Di Penanda 1 terbaca arus di posisi kursor bernilai 4.82 A. Sekalipun ini belum tentu adalah arus maksimum setelah lewat masa startup transient, nilainya tidak akan jauh berbeda. Tetapi lihatlah Penanda 2, di power stage yang tentu saja open-loop untuk sebuah flyback converter, kemungkinan adanya overshoot seperti ini tidak bisa diabaikan begitu saja. Hal yang berbeda untuk flyback converter yang di dalamnya telah terdapat IC regulator. IC komersial yang baik akan mengatur agar saat startup dan shutdown, tegangan dan arus di sistem tetap terkendali dalam batas aman.
Jika kurva di Penanda 2 diperbesar seperti di pane di atasnya, maka bentuk gelombang akan lebih jelas, berikut batas-batasnya. Agar proporsional, tetap perlu diingat bahwa overshoot di Gambar 31 terjadi dalam rentang waktu yang sangat singkat. Meskipun begitu untuk meminimalkan risiko, lebih baik mencari transistor yang mampu mengendalikan nilai arus yang cukup besar. Misalnya MOSFET IRLB3034pbf memiliki rating ID / Continuous Drain Current (arus drain) sebesar 195 A saat bekerja dengan suhu case 25 °C.
Sebagai pembanding, berikut adalah test report untuk sistem fisik konverter yang telah dilengkapi dengan IC regulator. Dapat dilihat bahwa meskipun tegangan input masuk dalam bentuk step (diukur dalam 2 ms/div) tetapi tegangan output tidak mengalami overshoot. Bandingkan dengan rangkaian power stage yang overshoot-nya terdeteksi sampai ke output.
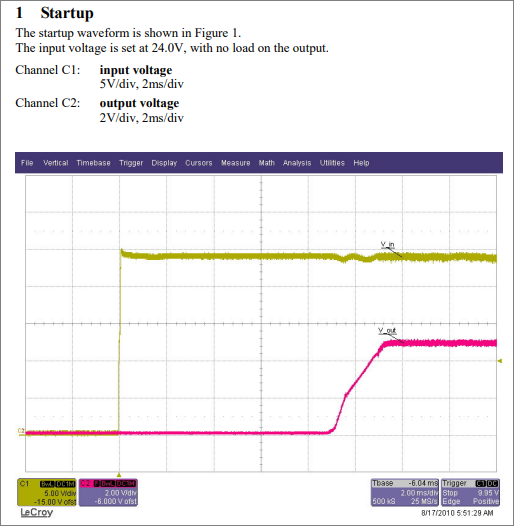Gambar 32. Contoh laporan pengujian startup dari flyback converter.
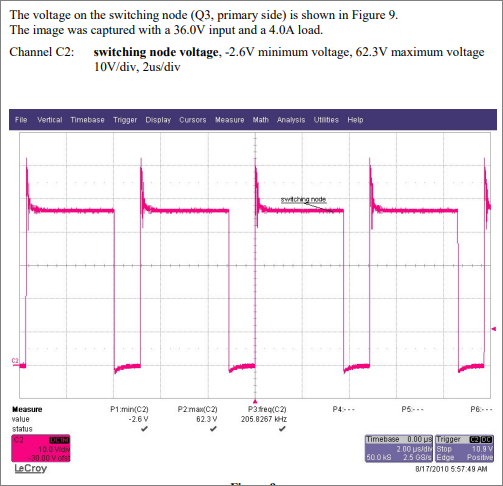Gambar 33. Contoh laporan pengujian MOSFET dari flyback converter.
Perhitungan (7): Perhitungan rating flyback transformer (konfigurasi alternatif 2)
Nilai RMS untuk komponen flyback transformer juga perlu diperhatikan, karena akan berkaitan dengan nilai disipasi daya (link).
Sebelum menghitung arus RMS, akan dihitung terlebih dahulu nilai arus puncak pada sisi primer. Persamaan yang dipergunakan sama seperti salah satu persamaan sebelumnya, hanya saja peruntukan dan notasinya yang berbeda. Persamaan sebelumnya:
\(\LARGE I_{LIM}\,min = \left( I_{OUT}\,max \times \frac {V_{OUT} + V_D} {V_{IN}\,min\times D\,max \times \eta _{EST}} \right) + \frac{I_{RIPPLE}}{2}\)Nilai yang dicari saat ini adalah IPRI peak:
\(\LARGE I_{PRI}\,peak = I_{LIM}\,min\)Sehingga:
\(\LARGE I_{PRI}\,peak = \left( I_{OUT}\,max \times \frac {V_{OUT} + V_D} {V_{IN}\,min\times D\,max \times \eta _{EST}} \right) + \frac{I_{RIPPLE}}{2}\)Jika nilai efisiensi ηEST yang dipakai adalah 100%:
\(\LARGE I_{PRI}\,peak = \left( 4 \times \frac {5 + 0.7} {9 \times 0.5601 \times 1} \right)+ \frac{0.9950604}{2}\approx 5.02\)Arus yang sama yang melewati drain di MOSFET juga melewati kumparan fisik sisi primer dari flyback transformer (yang sebenarnya magnetizing inductance), yaitu 5.02 A (jika dianggap 100% efisien).
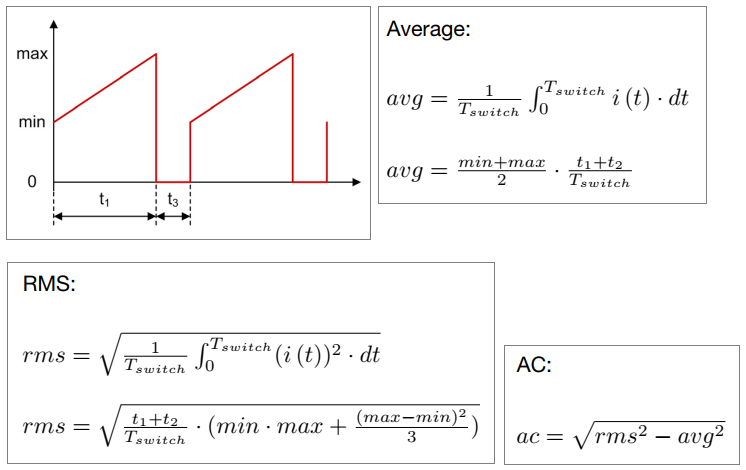Gambar 34. Positive triangular waveforms with offset [sumber].
\(\LARGE I_{PRI}\,min = I_{PRI}\,max – I_{RIPPLE} = I_{PRI}\,peak – I_{RIPPLE}\) \(\LARGE I_{PRI}\,min = 5.02 – 0.9950604 = 4.0249396\)
IPRI min ≈ 4.03 A
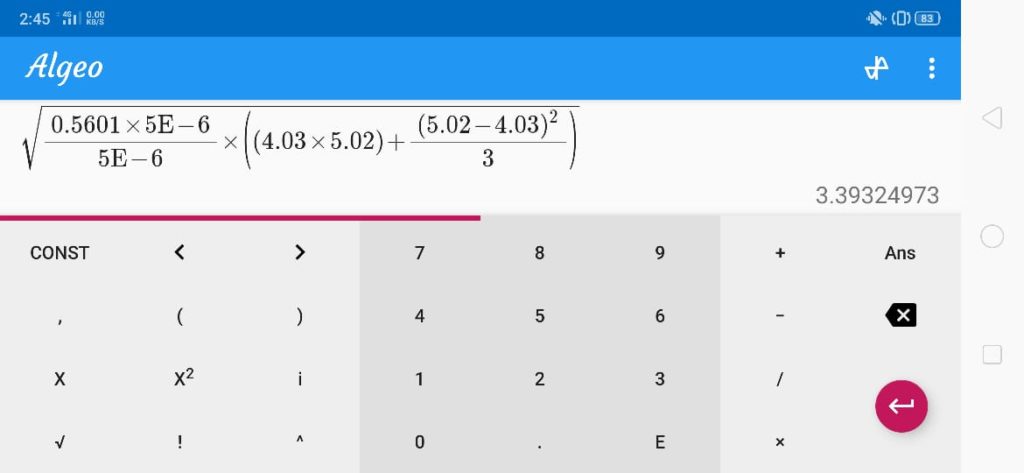
Terdapat beberapa turunan persamaan yang berbeda untuk menghitung nilai RMS, sekalipun intinya akan sama saja. Dimulai dari persamaan seperti di Gambar 34, nilai IPRIrms dapat dihitung sebagai berikut:
\(\LARGE I_{PRI}\,rms = \sqrt{ \frac { (0.5601 \times 5\,\mu)+0}{5\,\mu} \cdot \left( (4.03 \times 5.02) + \frac{(5.02-4.03)^{2}}{3} \right ) }\)
IPRI rms ≈ 3.39 A
\(\LARGE I_{PRI}\,avg= \left( \frac{4.03+5.02}{2}\right) \cdot \left(\frac{(0.5601\times5\,\mu)+0}{5\,\mu} \right )\) \(\LARGE I_{PRI}\,avg= 2.5344525 \;\textrm A\)IPRI avg ≈ 2.53 A
\(\LARGE I_{PRI}\,ac= \sqrt{3.39^2 – 2.53^2} = 2.25636876\)IPRI ac ≈ 2.26 A
Persamaan lain yang bisa dipakai untuk mencari nilai arus RMS didapat dari sumber di link ini, contoh:
\(\LARGE I_{PRI}\,rms = \sqrt{D \times \left(\left( \frac{V_{OUT}\times I_{OUT}}{V_{IN}\times D} \right )^2+\frac{(I_{RIPPLE})^2}{3} \right ) }\) \(\LARGE I_{PRI}\,rms = \sqrt{0.56005279 \times \left(\left( \frac{5\times 4}{9\times 0.56005279 } \right )^2+\frac{(0.9950604)^2}{3} \right ) }\)IPRI rms = 3.41234256 ≈ 3.41 A
Nilai hasil perhitungan ini berbeda bila dibandingkan dengan hasil perhitungan sebelumnya dengan persamaan lain. Ini adalah contoh kasus adanya selisih perhitungan untuk persamaan yang diatur ulang, dikarenakan pembulatan. Jika nilai IOUT diubah menjadi 3.97741585 A, maka hasil perhitungan arus primer rms akan menjadi:
\(\LARGE I_{PRI}\,rms = \sqrt{0.56005279 \times \left(\left( \frac{5\times 3.97741585}{9\times 0.56005279 } \right )^2+\frac{(0.9950604)^2}{3} \right ) }\)IPRI rms = 3.39338304 ≈ 3.39 A
Di perancangan elektronika selisih 1 mV atau 1 mA memang bisa menjadi masalah. Tetapi secara proporsional kita perlu tetap melihat ‘kasus-per-kasus’, karena kadang-kadang selisih nilai masih masuk dalam toleransi. Juga karena pendekatan ‘good enough’ sering sudah cukup untuk menyelesaikan masalah. Semua hasil perhitungan di atas dapat dibandingkan dengan perhitungan oleh PSD di Gambar 35.
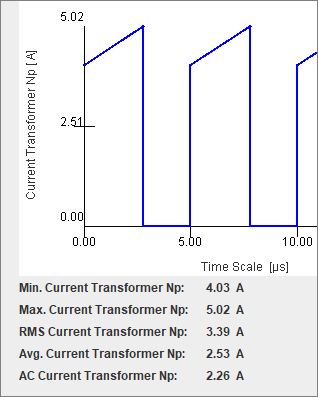Gambar 35. Hasil simulasi sisi primer trafo.
Untuk sisi sekunder, nilai-nilai untuk arus juga bisa didapat dihitung sebagai berikut.
Karena power stage ini dirancang untuk mode operasi CCM, maka persamaan untuk perbandingan arus dan tegangan sisi primer dengan sisi sekunder masih berlaku.
\(\LARGE I_{SEC}\,min= I_{PRI}\,min \times \frac{n_p}{n_s}\) \(\LARGE I_{SEC}\,min= 4.0249396 \,\textrm A \times \frac{2.01}{1} = 8.0901286 \,\textrm A\)ISEC min ≈ 8.09 A
\(\LARGE I_{SEC}\,max= (I_{PRI}\,max + I_{RIPPLE}) \times \frac{n_p}{n_s}\) \(\LARGE I_{SEC}\,max= (4.0249396 \,\textrm A + 0.9950604 \,\textrm A) \times \frac{2.01}{1}=10.0902 \,\textrm A\)ISEC max ≈ 10.09 A
Ada persamaan lain yang juga bisa dipakai untuk menghitung parameter yang sama. Untuk mempersingkat penulisan, variabel VO di dua persamaan berikut sebenarnya adalah VO+VD , sehingga ditulis sebagai berikut :
\(\LARGE I_{L}\,min=\left( I_O \times \left(1+\frac{n \times V_o}{V_{IN}} \right ) \right )- \left(\left(\frac{V_{IN}\times T}{2 \times n \times L} \right) \times \left( \frac{ n \times V_o}{V_{IN}+(n \times V_O)} \right) \right )\)
ISEC min ≈ 8.09 A
\(\LARGE I_{L}\,max=\left( I_O \times \left(1+\frac{n \times V_o}{V_{IN}} \right ) \right )+ \left(\left(\frac{V_{IN}\times T}{2 \times n \times L} \right) \times \left( \frac{ n \times V_o}{V_{IN}+(n \times V_O)} \right) \right )\)
ISEC max ≈ 10.09 A
\(\LARGE I_{SEC}\,rms = \sqrt{ \frac { ((1-0.5601) \times 5\,\mu)+0}{5\,\mu} \cdot \left( (8.09 \times 10.09) + \frac{(10.09-8.09)^{2}}{3} \right ) }\) \(\LARGE I_{SEC}\,rms = 6.0410872\)ISEC rms ≈ 6.04 A
Persamaan lain yang bisa dipakai untuk mencari nilai arus RMS trafo sisi sekunder didapat dari sumber di link ini, contoh:
\(\LARGE I_{SEC}\,rms= \sqrt{\frac{(1-D)}{3} \times \left( \left( 3\cdot \left(\frac{I_{OUT}}{1-D}\right)^2\right)+ \frac{(I_{RIPPLE} \times \textrm {Np2s})^2}{4} \right )}\) \(\LARGE I_{SEC}\,rms= \sqrt{\frac{(1-0.5601)}{3} \times \left( \left( 3\cdot \left(\frac{4}{1-0.5601}\right)^2\right)+ \frac{(0.9950604 \times \textrm {2.01})^2}{4} \right )}\)ISEC rms = 6.04305771 A ≈ 6.04 A
Perhitungan untuk average dan ac sisi sekunder dapat dilakukan dengan cara yang sama dengan sisi primer.
Saya tidak menyarankan untuk melakukan perhitungan ISEC rms dengan menggunakan Persamaan (13) di Gambar 12 di halaman (link), sampai nanti didapatkan penjelasan yang memadai. Jika dikehendki silakan dicoba dan dibandingkan hasilnya.
Kesemua hasil perhitungan manual untuk sisi sekunder trafo bisa dibandingkan dengan perhitungan oleh PSD. Ada banyak contoh serupa ini di berbagai dokumen sejenis application note, dapat coba dicari dengan tambahan kata-kata kunci ‘transformer design’.
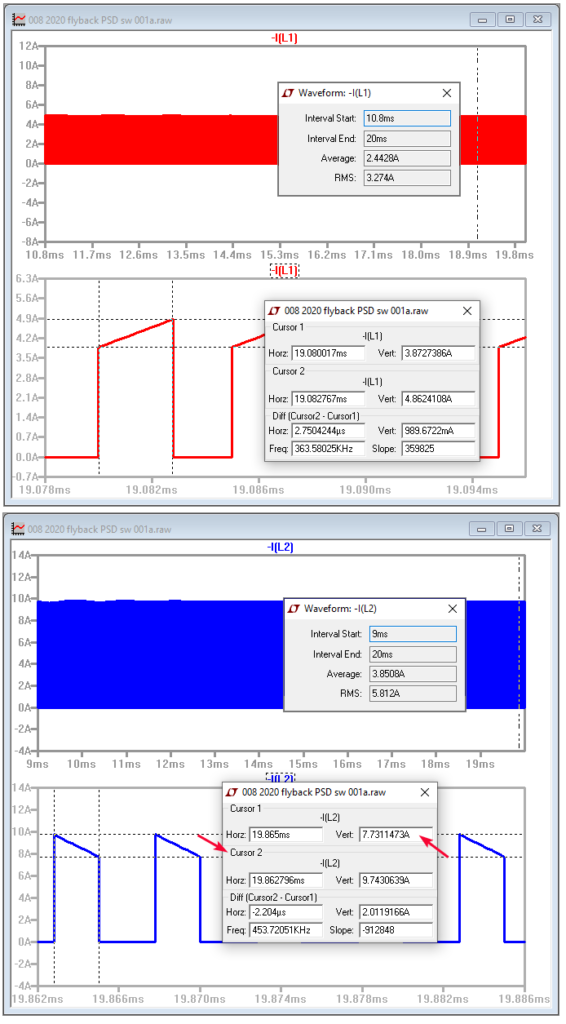Gambar 36. Hasil simulasi LTspice.
Detail hasil simulasi di Gambar 36, bisa dibandingkan dengan hasil perhitungan manual dan hasil perhitungan / simulasi PSD.
Perhitungan (8): Nilai kritis CCM ke DCM, (konfigurasi alternatif 2)
Contoh rangkaian power stage yang dihitung di halaman ini dirancang untuk bekerja di mode CCM. Namun demikian seperti banyak hal lain dalam rancangan, selalu ada prasyarat agar kondisi terpenuhi. Berdasarkan definisi, jika arus induktor (yang untuk flyback transformer ada di sisi primer) sempat turun sampai 0 A maka kondisi berubah dari mode CCM ke DCM. Untuk flyback converter topology, ini sedikit pelik dan perlu tambahan penjelasan. Yang dimaksud sebenarnya bukanlah arus sisi primer trafo yang disakelar oleh switch (seperti MOSFET). Tetapi adalah magnetizing current yang kadang-kadang istilahnya memang dipertukarkan dengan arus sisi primer trafo.
\(\LARGE I_{OUT}\,crit = \frac{V_{IN}^2 \times D_{CCM}^2}{2 \times L_{PRI} \times f_{SW} \times V_{OUT}}\) \(\LARGE I_{OUT}\,crit = \frac{V_{IN}^2 \times D_{CCM}^2}{2 \times L_{PRI} \times f_{SW} \times (V_{OUT}+V_D)}\)LPRI = LM
\(\LARGE I_{OUT}\,crit = \frac{9^2 \times 0.5601^2}{2 \times 25.32\,\mu \times 200000 \times (5+0.7)}=0.44016\)IOUT critical = 0.44016 A ≈ 0.44 A
Arus yang lebih mudah untuk diukur dan dilihat, adalah arus trafo sisi primer yang juga arus sakelar (MOSFET) seperti di Gambar 37. Dalam bahasa informal kurva arus ini dapat digambarkan memiliki tiga sisi; sisi sebelah kiri, sisi sebelah kanan, dan sisi bagian atas yang berbentuk diagonal (slope/ramp). Ini bisa disebut sebagai positive triangular waveform with offset, sebagaimana di Texas Instruments literature. Sisi sebelah kiri disebut minimum primary current, sisi sebelah kanan disebut maximum primary current. Sisi sebelah atas yang berupa positive slope / positive ramp, disebut sebagai increasing current (kebalikannya adalah decreasing current seperti di sisi sekunder trafo).
Dalam mode operasi CCM, nilai minimum primary current di trafo sisi primer ini tidak pernah turun sampai nol ampere. Untuk pembandingan visual, lihat Gambar 37. Gelombang dengan warna kuning adalah arus sisi primer trafo yang merupakan arus saat arus keluaran merupakan arus terbesar dari ketiga arus uji.
\(\LARGE I_{PRI}\,min=\left( \frac{(V_{OUT}+V_D)\cdot I_{OUT}} {V_{IN}\cdot f_{SW}\cdot t_{ON}} \right)-\left(\frac{1}{2}\cdot I_{RIPPLE} \right )\)Persamaan ini serupa dengan persamaan sebelumnya,
\(\LARGE I_{PRI}\,peak = \left( I_{OUT}\,max \times \frac {V_{OUT} + V_D} {V_{IN}\,min\times D\,max \times \eta _{EST}} \right) + \frac{I_{RIPPLE}}{2}\)Contoh perhitungan:
\(\LARGE I_{PRI}\,min=\left( \frac{(5+0.7)\cdot 4} {9\cdot 200E3 \cdot 2.80E-6} \right)-\left(\frac{1}{2}\cdot 0.9950604 \right )\) \(\LARGE I_{PRI}\,min= 4.02627932 \approx 4.03 \,\textrm A\)Penyusunan ulang persamaan:
\(\LARGE I_{OUT}\,crit=\frac{(I_{PRI}+(\frac{1}{2}\cdot I_{RIPPLE}))\cdot V_{IN}\cdot D} {V_{OUT}+V_D}\) \(\LARGE I_{OUT}\,crit=\frac{(I_{PRI}+(\frac{1}{2}\cdot I_{RIPPLE}))\cdot V_{IN}\cdot f_{SW}\cdot t_{ON}} {V_{OUT}+V_D}\) \(\LARGE I_{OUT}\,crit=\frac{(4.02627932+(\frac{1}{2}\cdot 0.9950604))\cdot 9\cdot 200E3\cdot 2.80E-6} {5+0.7}=4\)Jika nilai IPRI turun sampai 0 A, dapat dicari nilai IOUT critical:
\(\LARGE I_{OUT}\,crit=\frac{(0.00+(\frac{1}{2}\cdot 0.9950604))\cdot 9\cdot 200E3\cdot 2.80E-6} {5+0.7}=0.43992144\)Nilai yang didapat akan sama dengan nilai perhitungan sebelumnya dengan persamaan lain
IOUT critical = 0.439921446 A ≈ 0.44 A
Jadi Gambar 37 dan Gambar 38 menunjukkan ciri perbedaan secara visual antara gelombang arus sisi primer trafo saat beroperasi dalam mode CCM dengan saat beroperasi dalam mode DCM. Perbedaan itu berasal dari fenomena yang dapat ditunjukkan dengan operasi perhitungan seperti yang telah dilakukan. Suatu flyback converter akan berubah dari mode operasi CCM ke DCM bila nilai minimum primary current = IPRI = 0 A. Jika parameter operasi lain diketahui maka nilai arus keluaran (IOUTcrit) saat minimum primary current = 0 A juga dapat dihitung. Dengan begitu jika nilai tegangan masukan, IRIPPLE, duty cycle (frekuensi operasi dan tON), VOUT tidak berubah, operasi dalam mode DCM bisa dihindari dengan mencegah penurunan arus beban sampai mendekatan IOUTcrit.
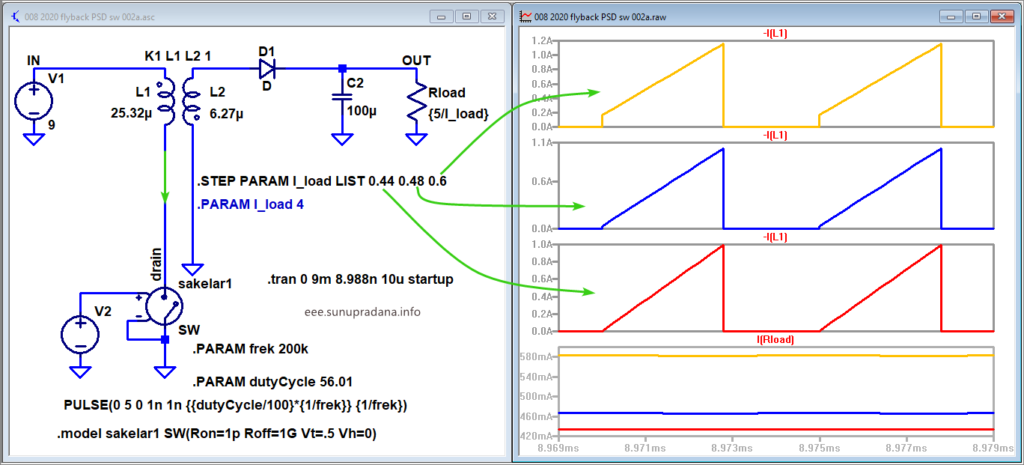Gambar 37. Simulasi stepping nilai arus keluaran.
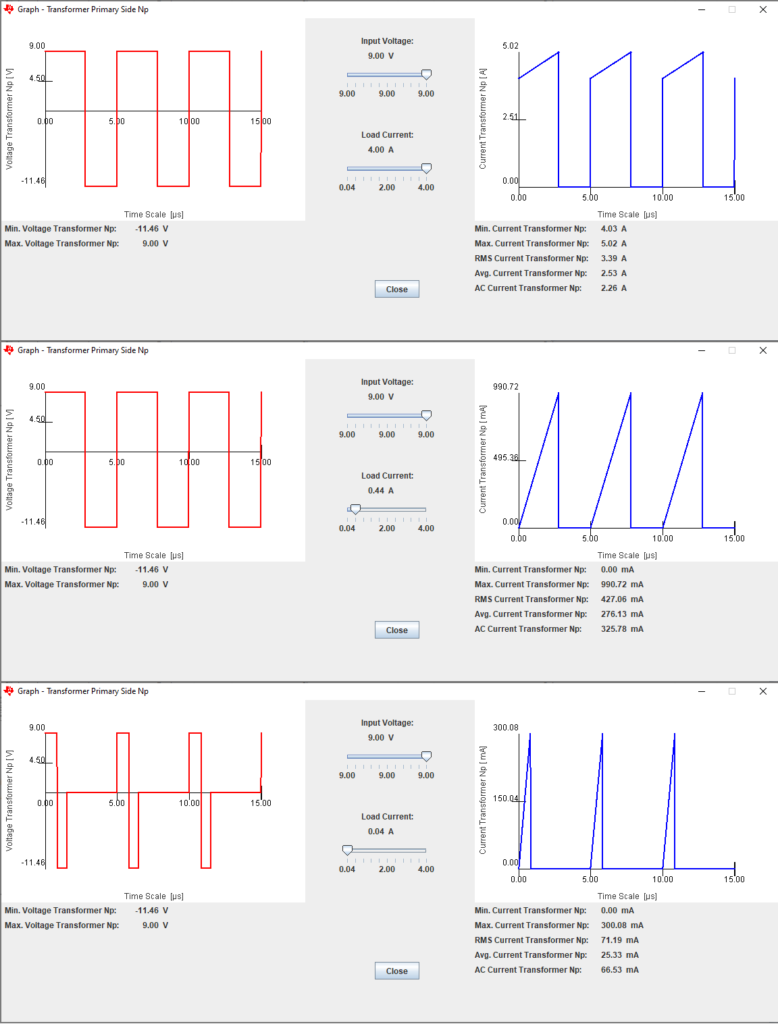
Gambar 37 adalah hasil simulasi pengaruh nilai arus output terhadap arus induktor di sisi primer flyback transformer. Ini adalah salah satu contoh hubungan korelasi dan kausalitas yang menjadi dasar dari engineering & technology. Perubahan besaran arus keluaran (misalnya karena perubaham impedansi beban) berpengaruh terhadap nilai arus di sisi primer trafo (yang dimaksud sebenarnya adalah induktor LM) yang bisa mengakibatkan perubahan mode operasi suatu flyback converter. Konverter ini dirancang untuk mengalirkan arus sebesar 4 A dengan tegangan 5 V ke beban.
Di Gambar 37 nilai arus keluaran yang turun sampai 0.6 A masih dapat menunjukkan kurva arus sisi primer trafo (juga arus MOSFET) dengan ciri mode operasi CCM. Tetapi untuk nilai batas arus kritis, diperlukan zoom-in agar ciri gelombang arus CCM dan DCM dapat lebih terlihat jelas seperti di Gambar 38.
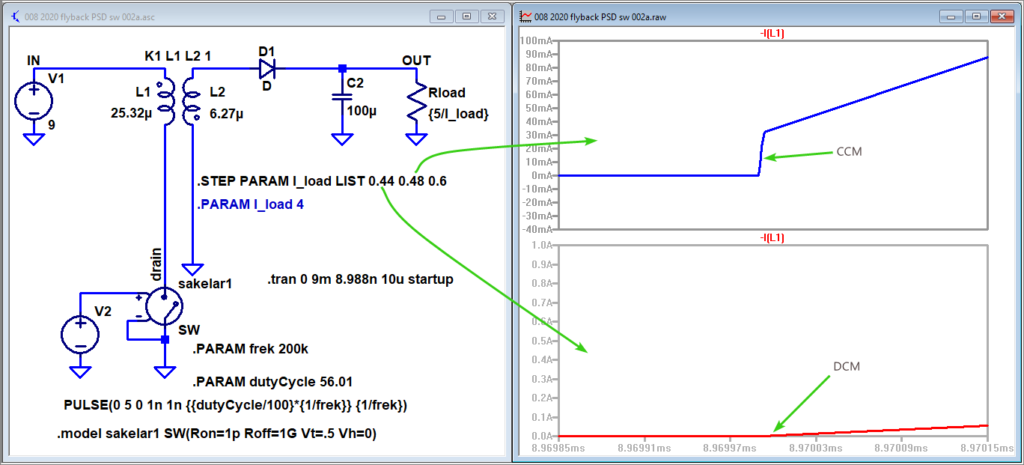Gambar 38. Batas arus keluaran kritis, peralihan CCM ke DCM.
Gambar 39. CCM-kritis-DCM.
The average current through a capacitor is zero and, likewise, the average voltage across an inductor is zero.
9: Capacitors and InductorsPerhatikan persamaan-persamaan berikut, dan lihat polanya:
\(\LARGE L_{crit}=\frac{n^2 \cdot (1-D)^2 \cdot R \cdot T}{2}\) \(\LARGE L_{crit}=\frac{(1-D)^2 \cdot R}{2 \cdot f} \times \left(\frac{Np}{Ns} \right)^2\)Dua persamaan di atas adalah persamaan yang memfasilitasi pencarian nilai L kritis sisi primer trafo untuk menjamin bahwa dengan variabel parameter yang dimasukkan, konverter akan tetap berada di mode operasi CCM. Jika nilai L di sisi primer (yang juga adalah LM) yang dipakai ternyata di bawah nilai yang direkomendasikan, maka akan berisiko untuk masuk ke mode DCM.
\(\LARGE L_{PRI} = \frac {V_{IN}\,max \times Dmin}{I_{RIPPLE} \times f_{SW}}\) \(\LARGE L_{PRI} = L_M=\frac{V_{IN}\cdot D \cdot T}{\Delta i_{L_m}} = \frac {V_{IN}\,max \times Dmin}{I_{RIPPLE} \times f_{SW}}\)Di beberapa sumber, kita juga akan menemui persamaan seperti dua persamaan di atas yang dipergunakan untuk mencari nilai induktansi. Keempatnya sebenarnya sebanding, sesuai peruntukan.
Dari keempat persamaan di atas, bisa disusun ulang untuk mencari nilai beban R kritis. Berdasarkan Hukum Ohm, dengan pengetahuan tentang nilai tegangan dan arus, dapat dicari nilai resistansi. Begitu pun nilai batas arus dapat diperkirakan berdasarkan tegangan dan nilai resistor.
\(\LARGE R = \frac{2 \times V_{IN} \times D}{n^2 \times (1-D)^2}\) \(\LARGE R = \frac{2 \times 9 \times 0.5601}{2.01^2 \times (1-0.5601)^2} \approx 12.90\)Sebagai contoh, untuk D=56.01% maka nilai resistansi kritis adalah 12.9 Ω, jika lebih besar dari itu maka nilai arus keluaran akan mengecil dan berisiko menyebabkan berpindahnya dari mode operasi CCM ke mode DCM. Tetapi perlu diingat ini hanyalah estimasi saja, untuk simulasi, nilai R bisa berselisih antara 2 Ω sampai 3 Ω dari hasil perhitungan.
Keempat persamaan itu juga bisa dipilah dan dipilih untuk diatur ulang dalam upaya mencoba mencari estimasi nilai Dkritis dengan tahapan sebagai berikut:
\(\LARGE \frac {(1-D)^2}{D}= \frac {2 \times V_{IN}}{n^2 \times R}\) \(\LARGE k = \frac {2 \times V_{IN}}{n^2 \times R}\) \(\LARGE D= \frac {2+k- \sqrt{k^2+(4\cdot k)}}{2}\)Sebagai contoh, rangkaian flyback converter ini dibuat dengan target sasaran nilai keluaran 5 V dengan arus 4 A. Dari kedua parameter itu dapat dihitung beban resistif sebagai uji coba, yaitu 1.25 Ω. Pertanyaannya dengan beban resistif sebesar ini, berapakah nilai duty cycle kritisnya? Dengan perhitungan berikut yang menggunakan persamaan di atas didapat hasil sekitar 18.59%. Sebagaimana disebutkan di banyak application note, nilai semacam ini hanyalah estimasi saja. Bahkan untuk simulasi, anda perlu memberi toleransi antara 2% sampai 3% dari D hasil perhitungan.
Untuk mencegah potensi kebingunan, berikut ini ada satu contoh yang menunjukkan perbedaan filosofi dua simulator dan dampaknya bagi pengguna. Yang pertama PSD, ini biasanya dipakai sebagai go-to simulator untuk power stage karena mudah dan cepat. Tetapi perlu diwaspadai cara kerjanya karena akan berbeda jika dilakukan simulasi yang menggunakan model SPICE komponen fisik, atau terlebih lagi saat nantinya benar-benar menggunakan komponen fisik.
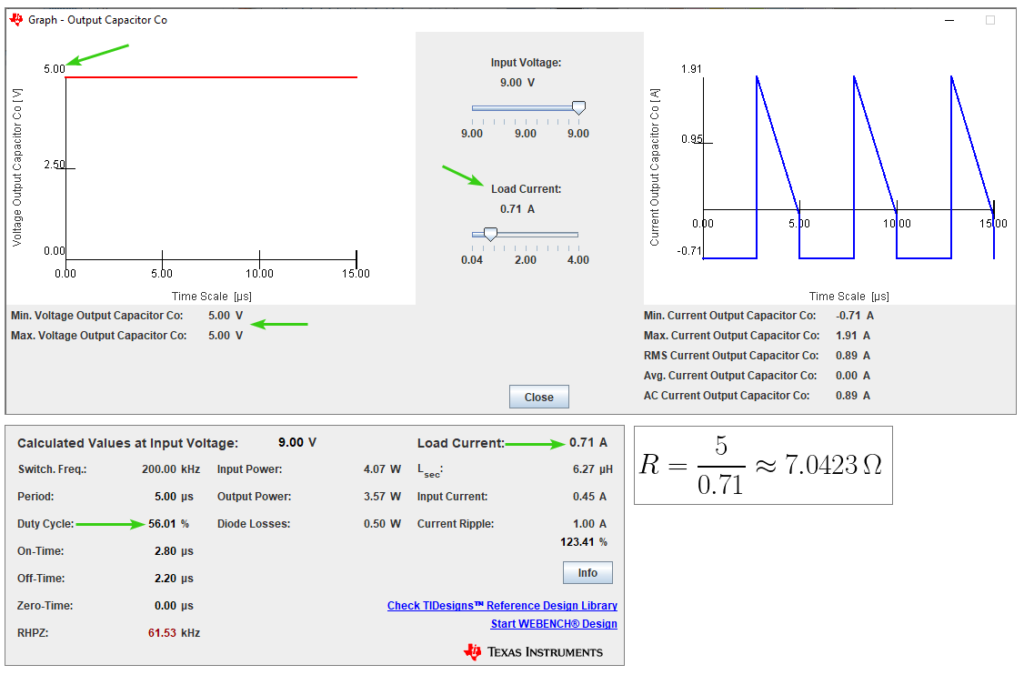Gambar 40. Perhitungan nilai resistor beban.
Level tegangan keluaran di simulasi PSD diatur konstan meskipun nilai duty cycle dan arus keluaran berubah, seperti di Gambar 40. Cara ini berbeda dengan simulator rangkaian yang lain. Mengikuti hasil dari PSD kalau dipergunakan nilai tegangan sebesar 5 V dan arus sebesar 0.71 A, maka akan diperoleh nilai R beban sebesar 7.04 Ohm.
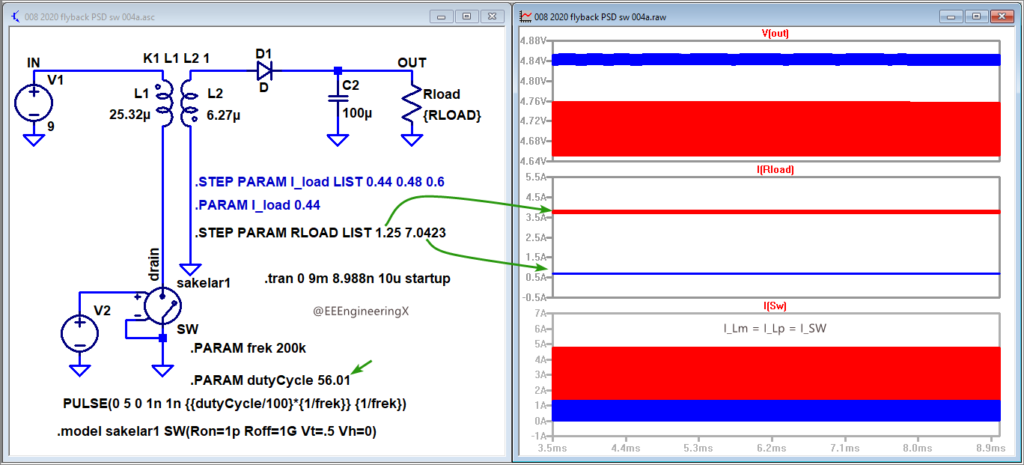Gambar 41. Pengaruh kenaikan nilai resistansi.
Gambar 41 menunjukkan pengaruh perubahan nilai resistansi pada hasil simulasi dengan LTspice. Sebagaimana sebuah power stage yang open-loop, nilai tegangan keluaran V(out) tentu tidak dapat dipertahankan konstan jika parameter rangkaian berubah.
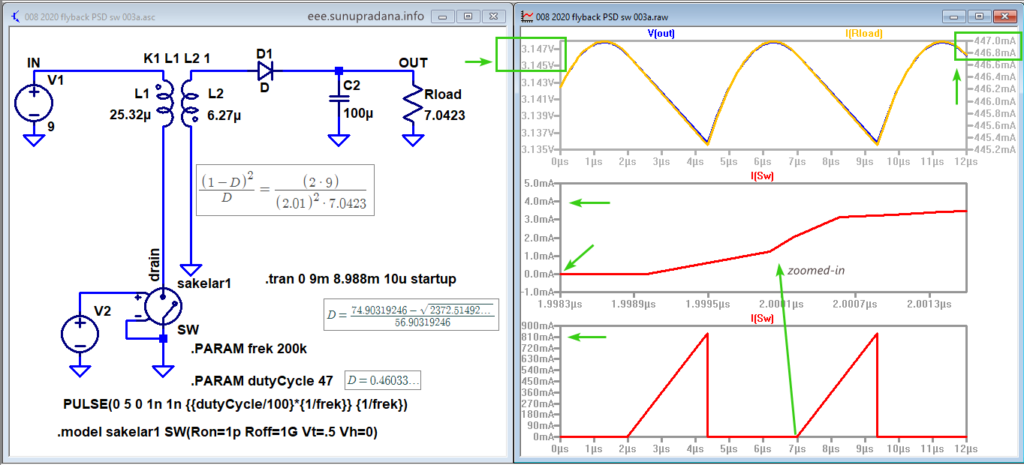Gambar 42. Percobaan simulasi D kritis.
Gambar 42 adalah contoh hasil simulasi untuk mencoba persamaan yang telah diturunkan sebelumnya. Nilai R tetap memakai 7.04 Ohm, tetapi nilai D diturunkan mendekati nilai kritisnya. Sengaja masih saya beri nilai 47% agar ciri peralihan masih dapat terlihat jika dilakukan pembesaran gambar, seperti di Gambar 42.
Persamaan berikut ini juga dapat dipakai untuk melihat korelasi antar parameter konverter. Tetapi perlu hati-hati untuk mempergunakannya karena bisa anda perhatikan bahwa nilai terbesar duty cycle adalah 1 (100%). Persamaan ini bisa dipakai untuk memeriksa balik hasil perhitungan dengan persamaan untuk mencari IOUT critical sebelumnya. Gunakan IOUT = IOUT critical = 0.44016 A ≈ 0.44 A .
\(\LARGE D_{DCM}=\sqrt{\frac{2 \times I_{OUT} \times f_{SW} \times L_{PRI} \times (V_{OUT}+V_D) }{(V_{IN}\,min)^2} }\)Perhitungan (9): Diode, (konfigurasi alternatif 2)
Diode yang dipakai di sistem utama (power stage) harus mampu mengakomodasi dua hal, tegangan breakdown dan disipasi daya.
\(\LARGE V_{BR} = V_{OUT} + (V_{IN}\, max \times \textrm {Np2s})\) \(\LARGE V_{BR} = 5+(9\times2.01)=23.09\) \(\LARGE P_D = I_{OUT} \times V_D = 4 \,\textrm A \times 0.7 \,\textrm V = 2.8 \,\textrm W\)Minimal diode Schottky yang akan dipakai mampu menahan tegangan balik sekitar 23.09 V dan melakukan disipasi daya 28 Watt.
Perhitungan (10): Output capacitor, (konfigurasi alternatif 2)
Menurut laporan hasil pengujian alat konverter di Gambar 16, untuk masukan sebesar 9 V nilai riak arus adalah sedikit di atas 50 mV, nilai riak yang sama yang coba dicapai di sini. Lihatlah juga Gambar 13 untuk skema rangkaian rancangan asli sistem.
\(\LARGE C_{OUT}> \frac{I_{OUT} \times D\,max}{V_{RIPPLE}\times f_{SW}}= \frac{4 \times 0.5601}{51E-3 \times 200E3} \approx 219.65\,\mu \textrm F\) \(\LARGE ESR<\frac{V_{RIPPLE}\times(1-D\,max)}{I_{OUT}}=\frac{51E-3\times(1-0.5601)}{4}\approx 5.61\,m\Omega\)Umumnya untuk mendapatkan nilai yang memadai, komponen kapasitor di sisi output biasanya dirangkai paralel dengan menggunakan beberapa kapasitor dari jenis yang berbeda. Mengingat masing-masing jenis kapasitor memiliki keunggulan masing-masing, misalnya untuk filtering frekuensi tinggi atau yang efektif untuk meratakan tegangan karena umumnya memiliki kapasitas besar.
Perhitungan (11): Input capacitor, (konfigurasi alternatif 2)
\(\LARGE I_{IN}\,DC= \frac{V_{OUT} \times I_{OUT}}{V_{IN} \times \eta _{EST}}=\frac{5\times4}{9 \times 0.8}\approx 2.78 \,\textrm A\) \(\LARGE C_{IN}>\frac{I_{IN}\,DC}{D\,max \times f_{SW} \times V_{IN}\,ripple\,%max \times V_{IN}\,min}\) \(\LARGE C_{IN}>\frac{2.78}{0.5601 \times 200E3 \times (10%) \times 9} \approx 27.57\,\mu \textrm F\)Sama halnya dengan kapasitor untuk output, kapasitor untuk input pun seringkali dipasang secara paralel.
Perhitungan (12): IRIPPLE dan LM, (konfigurasi alternatif 1)
Setelah selesai melihat sebagaian besar urutan perhitungan dari sudut pandang perancangan, maka di akhir ini saya kembali ke Perhitungan (1) dan Perhitungan (2) . Setelah membuktikan bagaimana parameter operasi di Gambar 27 diperoleh, sekarang kita coba melakukannya kembali untuk Gambar 26. Nilai duty cycle , tON, tOFF, periode, sudah didapatkan maka tinggal melanjutkan untuk riak arus, magnetizing inductance (Lm=Lp), dan Ls.
Bagian pertama ini dengan menggunakan masukan target riak arus sebesar 22% dan menghitung nilai riak arus dalam ampere.
\(\LARGE I_{RIPPLE}=\textrm{RIP%} \times \frac{V_{OUT} \times I_{OUT}}{V_{IN}\,max \times D_{min}}\) \(\LARGE I_{RIPPLE}=\textrm{RIP%} \times \frac{(V_{OUT}\,+\,V_D) \times I_{OUT}}{V_{IN}\,max \times Dmin}\) \(\LARGE I_{RIPPLE}= 0.22 \times \frac{(5+0.7) \times 4}{9 \times 0.5588} = 0.99737533\)Didapati bahwa jika D menjadi sebesar 55.88% maka nilai riak arus akan ≈ 0.997 A. Berikutnya dengan nilai ini akan dicari nilai magnetizing inductance (Lm=Lp=LPRI).
\(\LARGE L_{PRI} = \frac {V_{IN}\,max \times Dmin}{I_{RIPPLE} \times f_{SW}}\) \(\LARGE L_{PRI} = \frac {9 \times 0.5588}{0.99737533 \times 200\textrm{E}3} = 25.21217364\approx 25.21\,\mu\)Nilai induktansi primer yang direkomendasikan adalah 25.21 μH, tetapi perancang rangkaian memilih nilai pembulatan 25.00 μH. Sehingga riak arus dengan nilai induktor ini dapat dihitung ulang:
\(\LARGE I_{RIPPLE} = \frac {V_{IN}\,max \times Dmin}{L_{PRI} \times f_{SW}}\) \(\LARGE I_{RIPPLE} = \frac {9 \times 0.5588}{25E-6\times 200\textrm{E}3} = 1.00584\approx 1.01\,\textrm A\) \(\LARGE \textrm{RIP%}= I_{RIPPLE} \times \frac{V_{IN}\,max \times Dmin}{(V_{OUT}\,+\,V_D) \times I_{OUT}}\) \(\LARGE \textrm{RIP%}= 1.00584 \times \frac{9 \times 0.5588} {(5+0.7) \times 4} = 22.18671284\textrm % \approx 22.19 \textrm %\)Nilai riak arus 1 A yang berarti 22.19% sesuai dengan hasil perhitungan/simulasi PSD.
Perhitungan untuk nilai induktansi sisi sekunder trafo dapat dilakukan dengan menggunakan persamaan untuk trafo yang umum.
\(\LARGE L_{sec} = \left(\frac{N_s}{N_p}\right)^2 \times L_{pri}\) \(\LARGE L_{sec} = \left(\frac{1}{2}\right)^2 \times 25\,\mu \textrm H = 6.25 \,\mu \textrm H\)Nilai ini sama dengan hasil perhitungan PSD.
Demikian artikel yang memaparkan simulasi rangkaian untuk topologi flyback converter yang masih berupa power stage. Perkecualian adalah bagian paling awal yang meunjukkan bagaimana simulasi terhadap power stage flyback converter yang telah dilengkapi IC regulator sehingga sudah berubah dari open-loop menjadi closed-loop.
Di lain waktu akan dicoba disampaikan simulasi lain untuk sistem yang sudah menggunakan IC regulator/controller. Sementara itu, artikel lain bisa dibaca di halaman ini.
Mari sama-sama menjaga semangat belajar untuk diri sendiri dan untuk Indonesia yang lebih baik. Tampaknya seperti sudah menjadi hukum alam bahwa bangsa dan negara-negara yang terus menerus meningkatkan kemampuan untuk mengelola alam lah yang bisa lebih makmur bahkan daripada negara yang memiliki cadangan kekayaan alam itu sendiri.
Semangat!
font cache: Ψ α β π θ μ Φ φ ω Ω ° ~ ± ≈ ≠ ≡ ≤ ≥ ∞ ∫ • ∆