Jenis software (perangakat lunak) komputasi dapat digolongkan ke dalam beberapa bagian. Dua bagian yang menjadi perhatian untuk pembahasan kali ini adalah numerical analysis software dan computer algebra systems. Mesikipun sebagian software dapat melakukan keduanya (dua jenis pekerjaan matematis). Contoh dari numerical analysis software adalah MATLAB, Scilab dan GNU/Octave. Sedangkan Maxima termasuk ke dalam computer algebra systems.
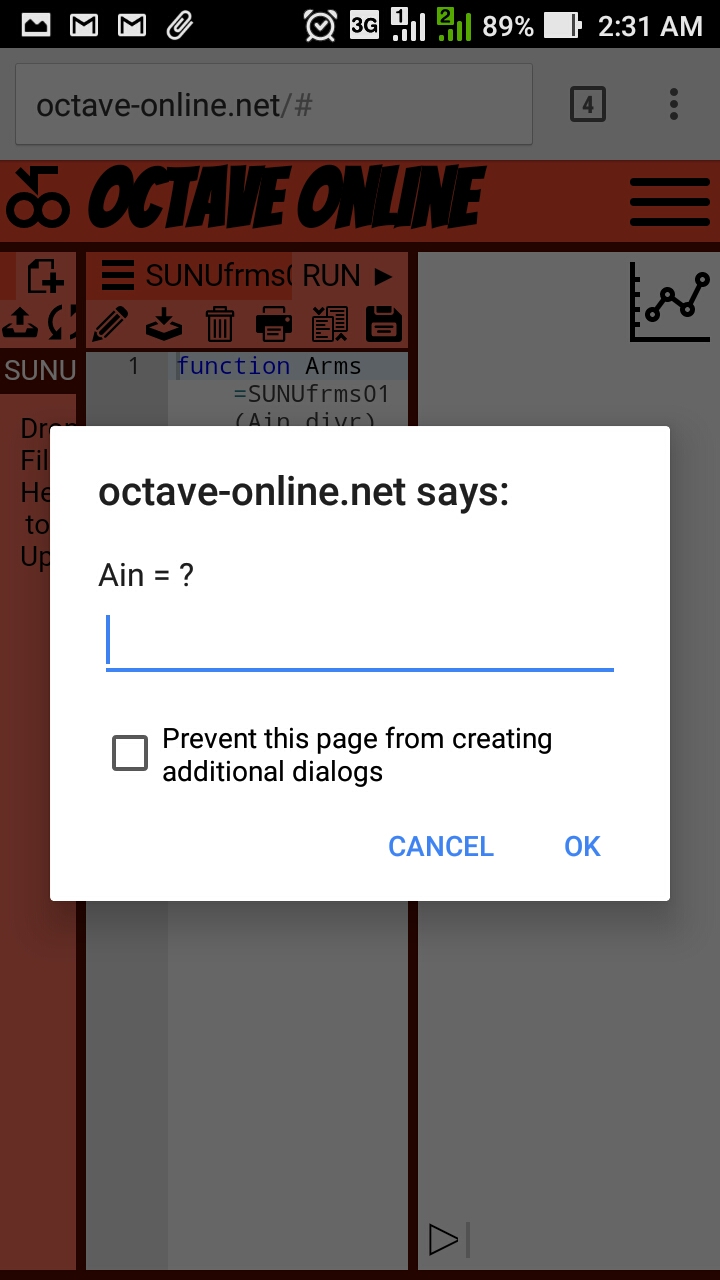
[/intense_panel] [su_panel border=”2px solid #CCFF00″ radius=”10″]Program komputer GNU/Octave (lazim hanya disebut sebagai Octave) dapat dipergunakan secara online maupun offline. Keuntungan mempergunakannya secara offline (sebagaimana banyak program komputer lainnya) adalah bahwa pengguna tidak terlalu tergantung pada kondisi koneksi Internet. Sedangkan keuntungan mempergunakan secara online adalah bahwa pengguna tidak perlu melakukan proses instalasi yang kadang-kadang tidak dapat dilakukan dengan lancar dan mudah. Pengguna juga tidak perlu melakukan pemeliharaan secara berkala (seperti melakukan update).
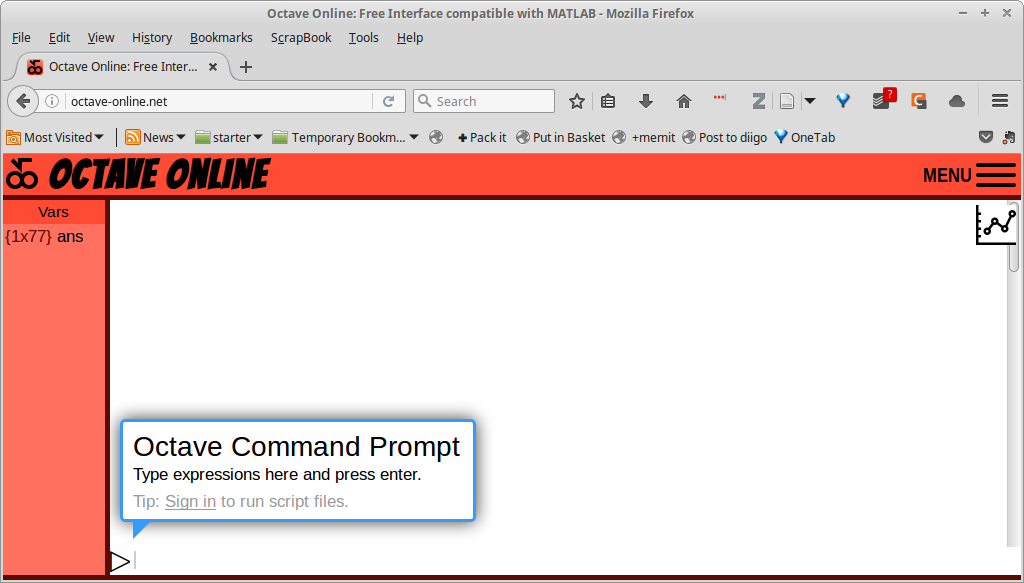 Gambar 1. Octave-online.net.
Gambar 1. Octave-online.net.
 Gambar 2. https://www.tutorialspoint.com/octave_terminal_online.php.
Gambar 2. https://www.tutorialspoint.com/octave_terminal_online.php.
 Gambar 3. https://www.rollapp.com/app/octave#.
Gambar 3. https://www.rollapp.com/app/octave#.
 Gambar 4. rollApp GNU/Octave
Gambar 4. rollApp GNU/Octave
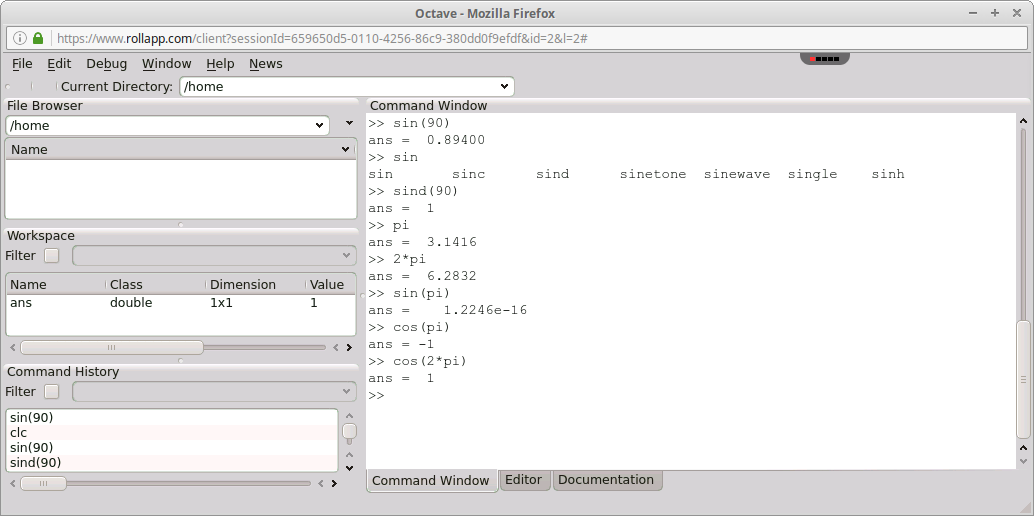 Gambar 5. rollApp
Gambar 5. rollApp
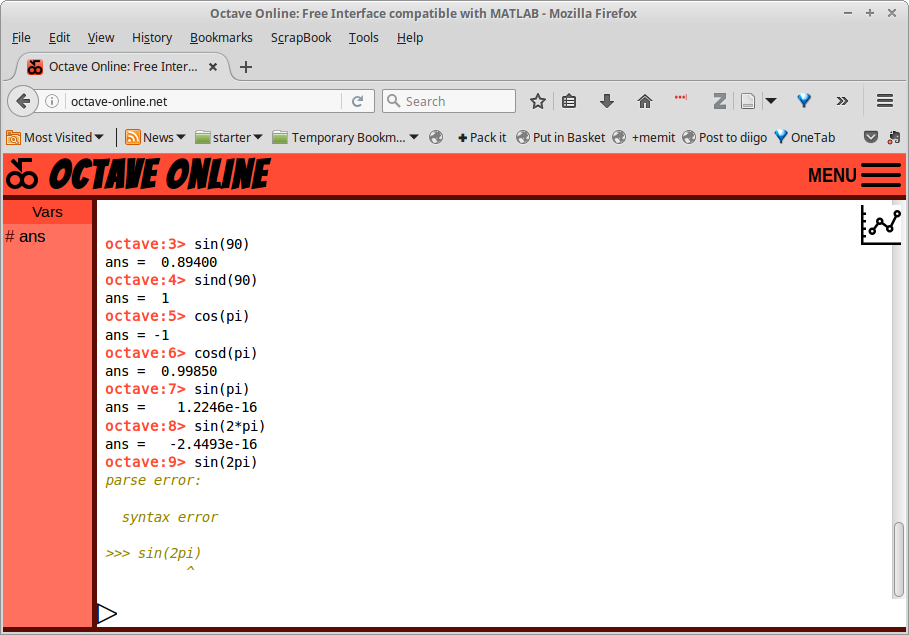 Gambar 6.
Gambar 6.
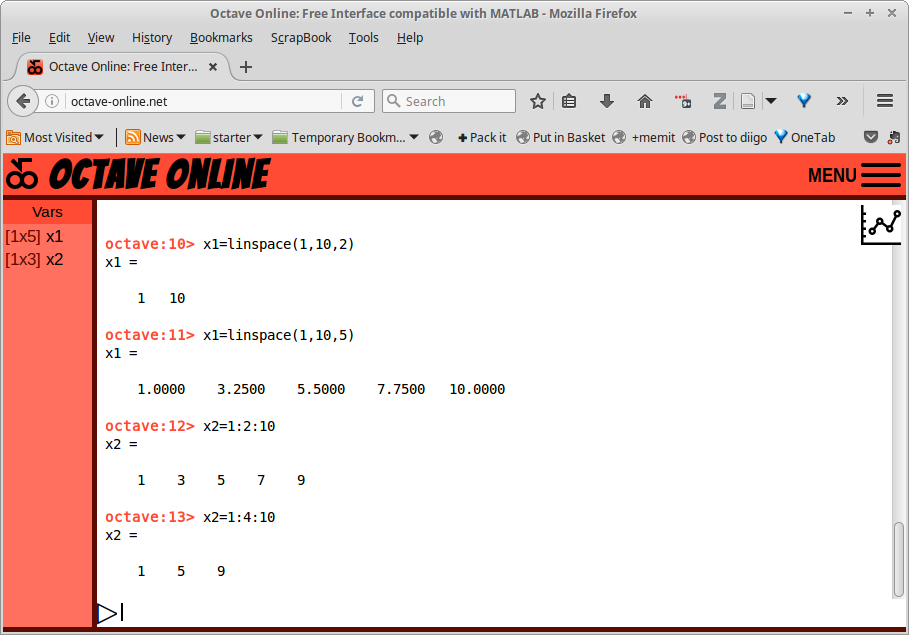 Gambar 7.
Gambar 7.
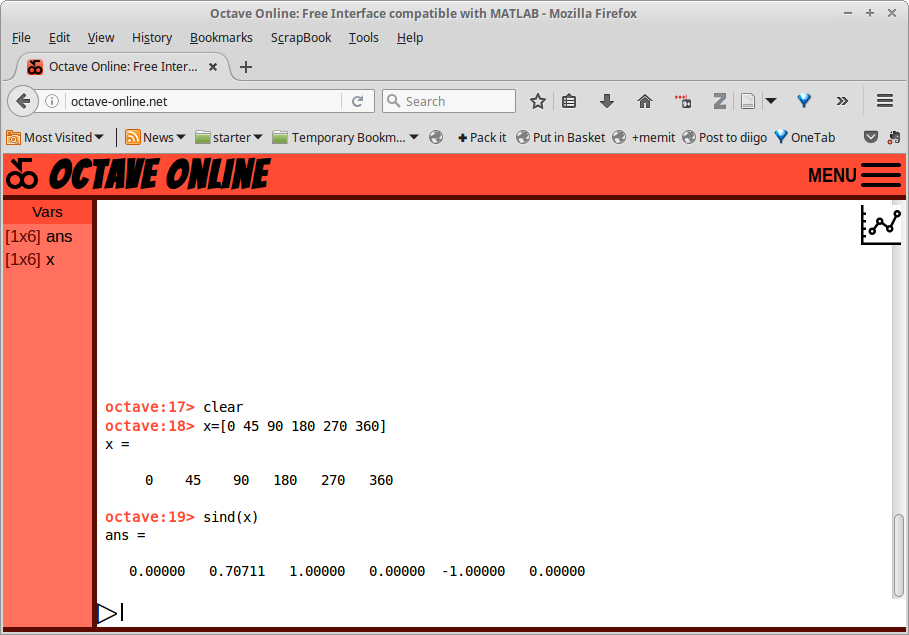 Gambar 8.
Gambar 8.
 Gambar 9.
Gambar 9.
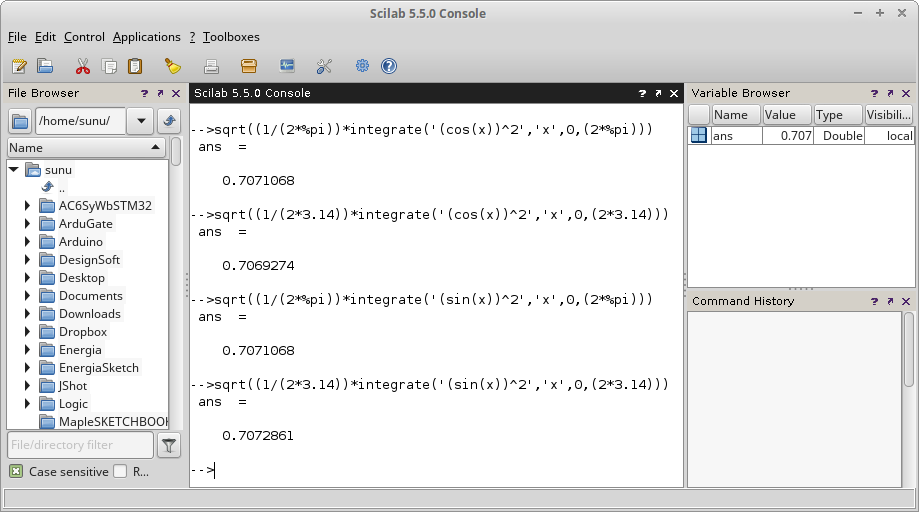 Gambar 10.
Gambar 10.
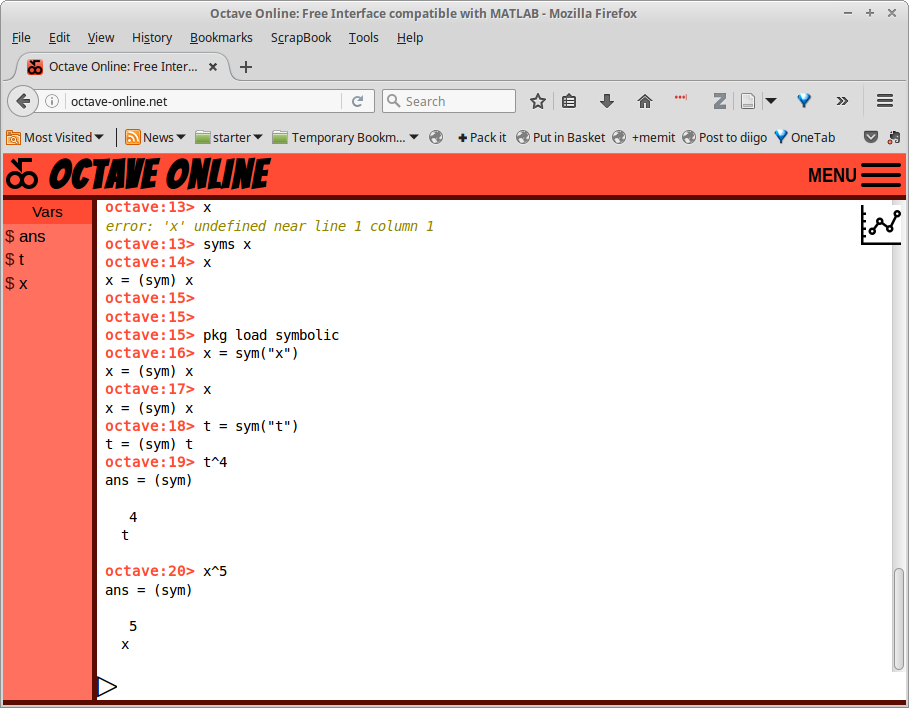 Gambar 11.
Gambar 11.
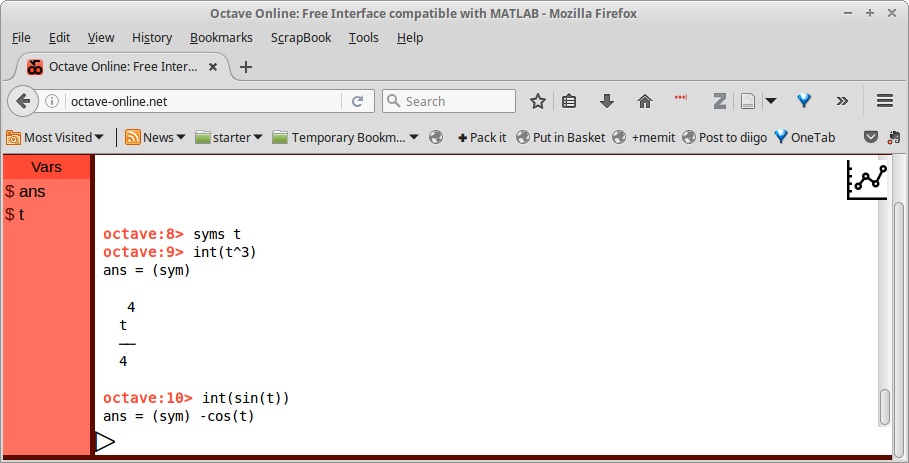 Gambar 12.
Gambar 12.
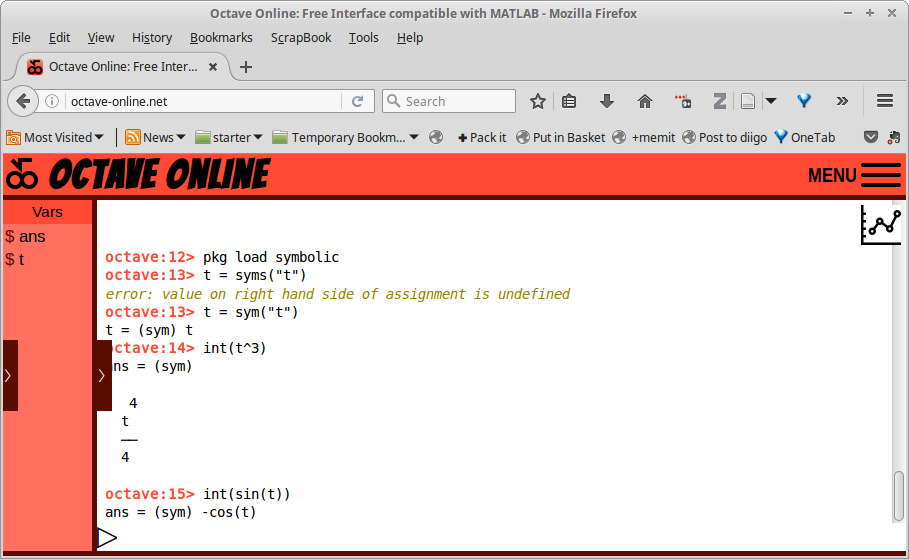 Gambar 13.
Gambar 13.
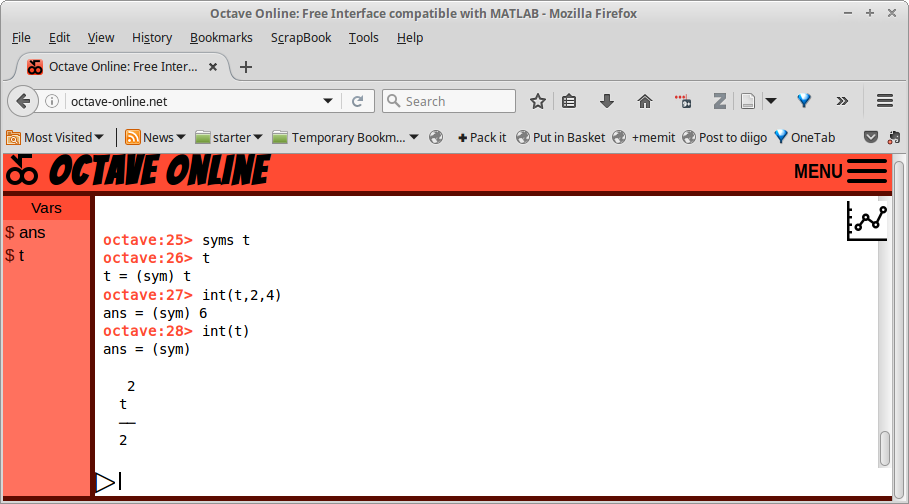 Gambar 14.
Gambar 14.
syms x a=int((sin(x))^2,0,2*pi) b = sqrt((1/(2*pi))*a)
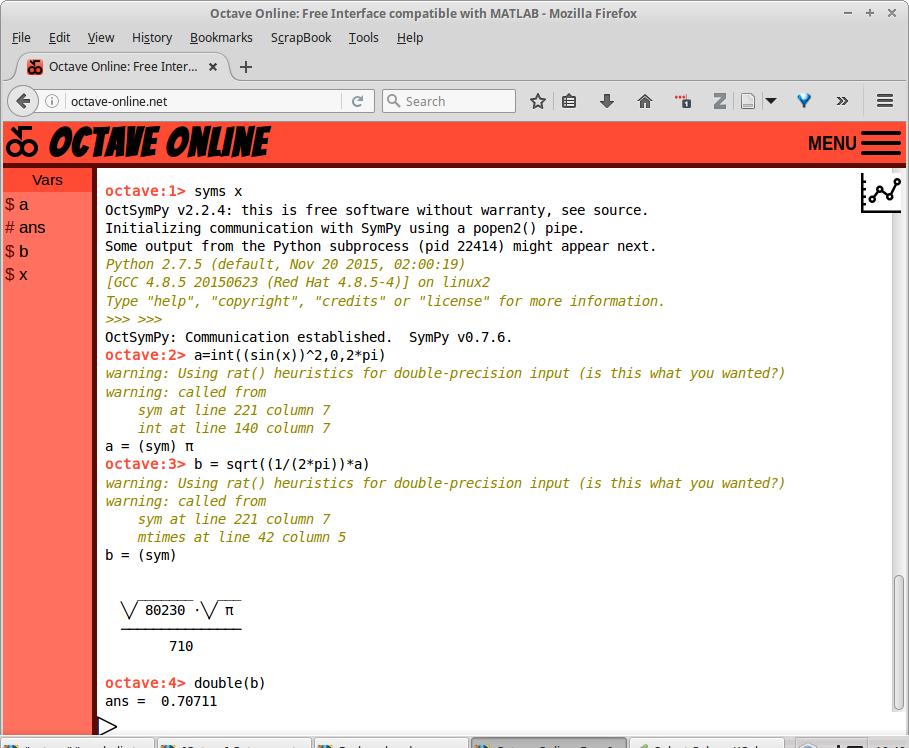 Gambar 15.
Gambar 15.
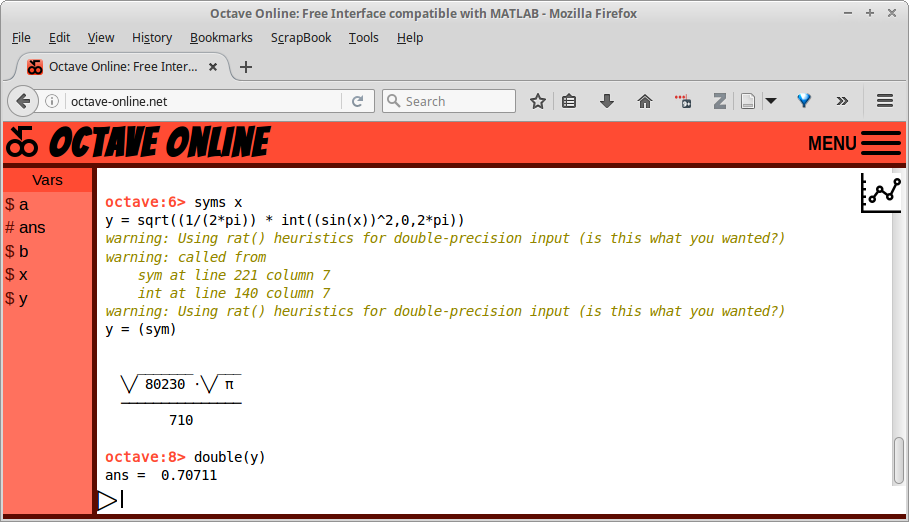 Gambar 16.
Gambar 16.
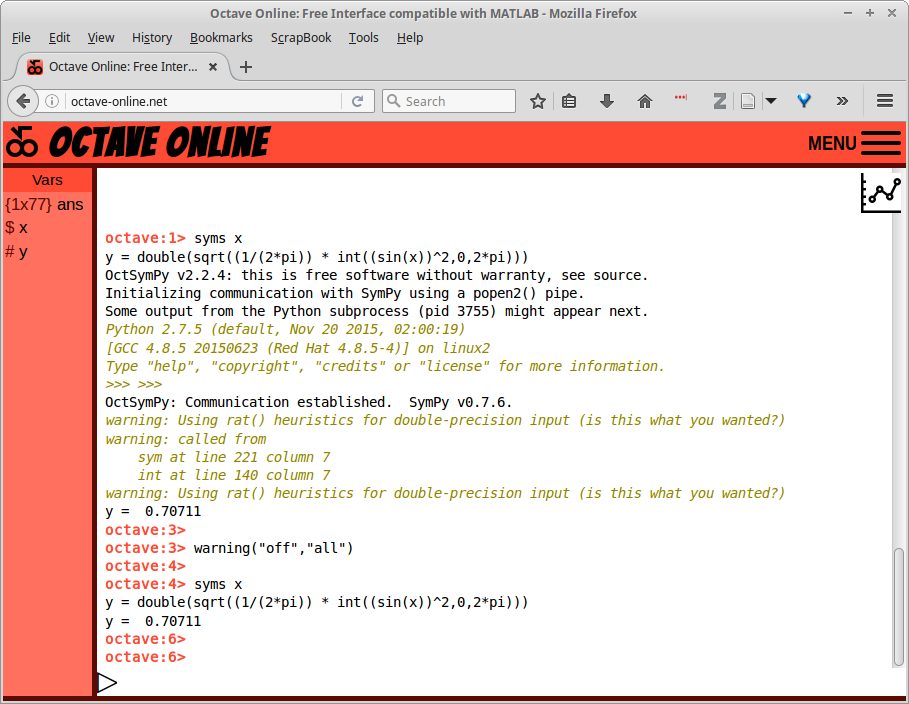 Gambar 17.
Gambar 17.
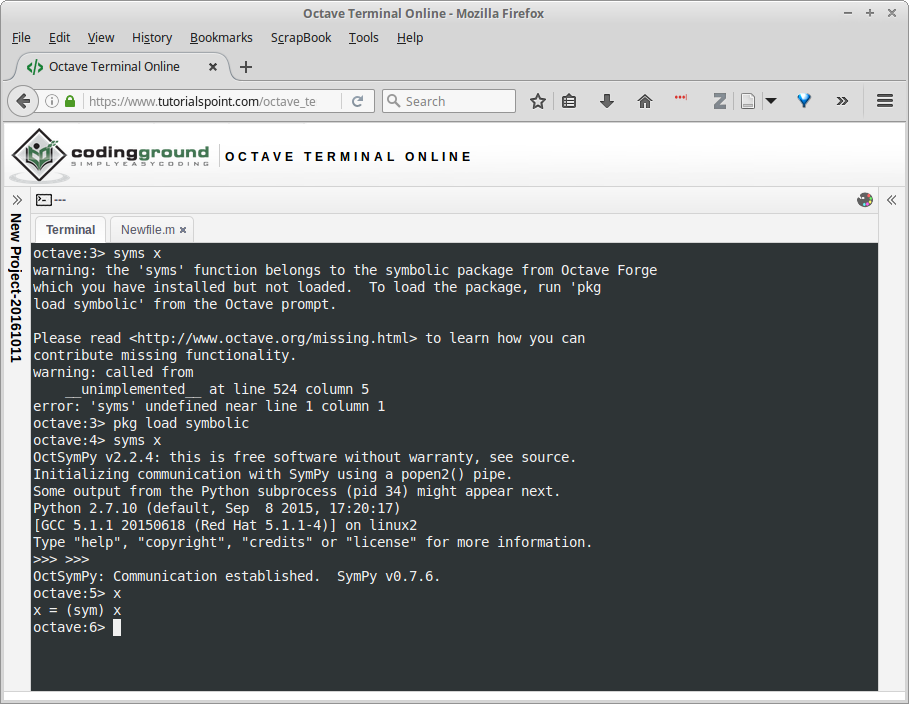 Gambar 18.
Gambar 18.
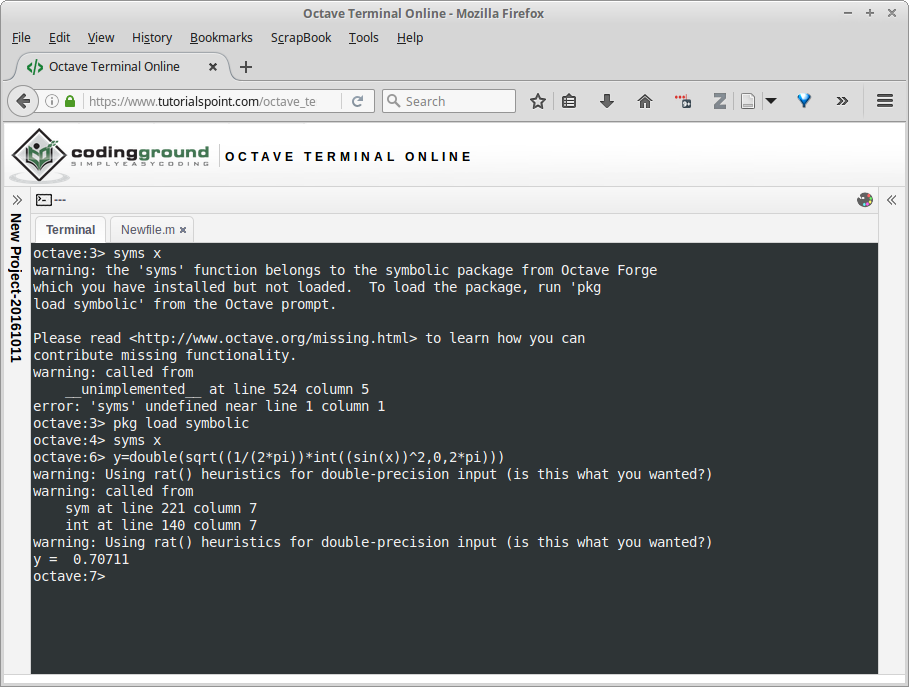 Gambar 19.[/su_panel]
[su_panel border=”2px solid #FF3300″ radius=”10″]
Gambar 19.[/su_panel]
[su_panel border=”2px solid #FF3300″ radius=”10″]
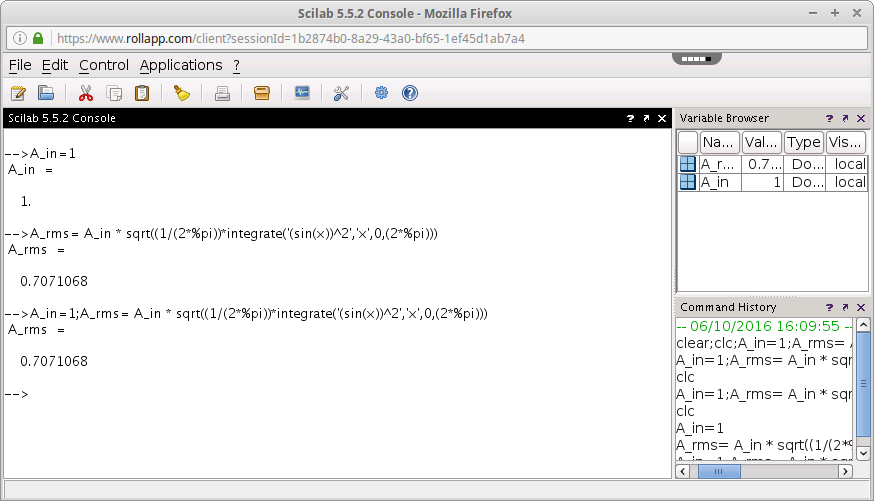 Gambar 20.
Gambar 20.
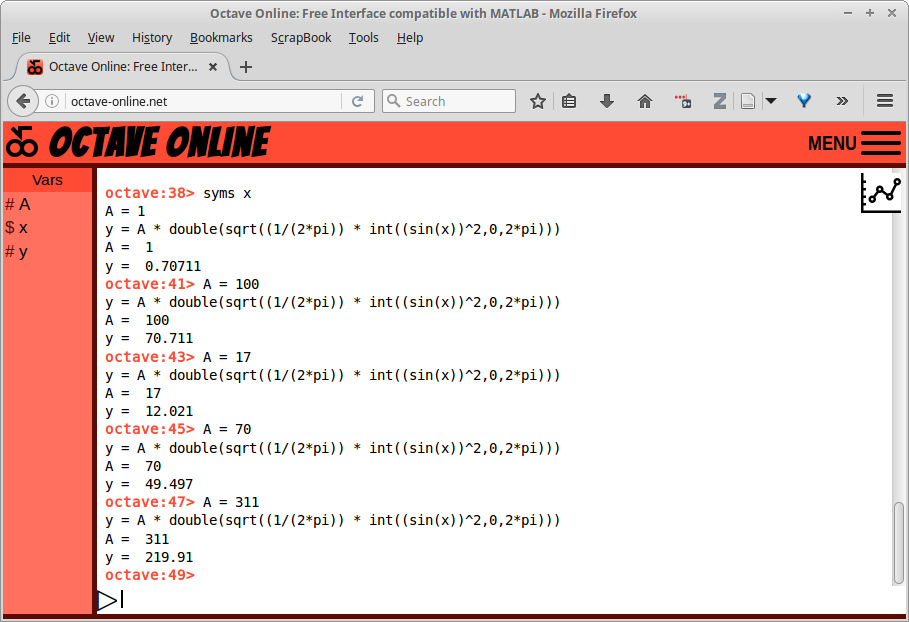 Gambar 21.
Gambar 21.
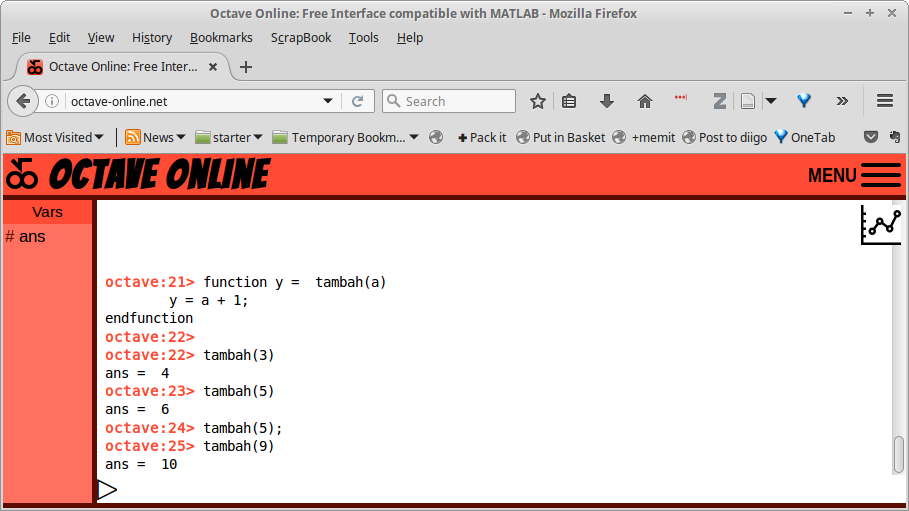 Gambar 22.
Gambar 22.
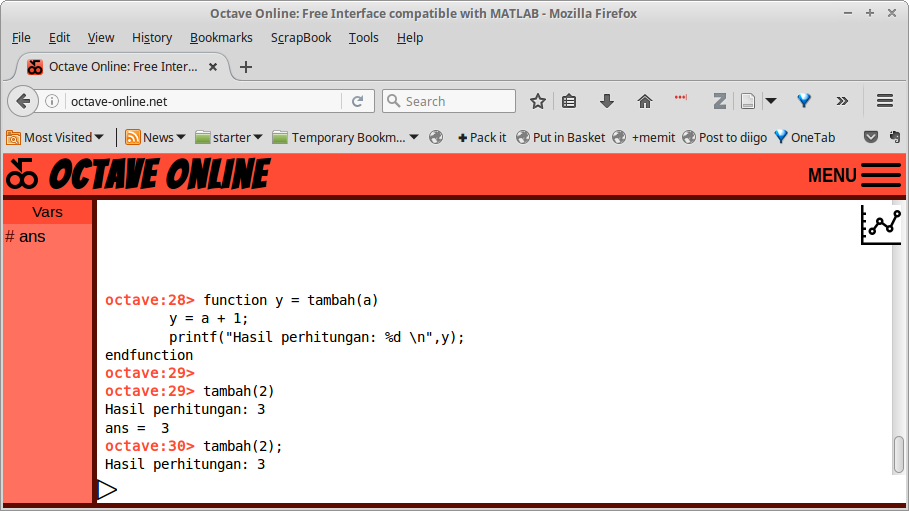 Gambar 23.
Gambar 23.
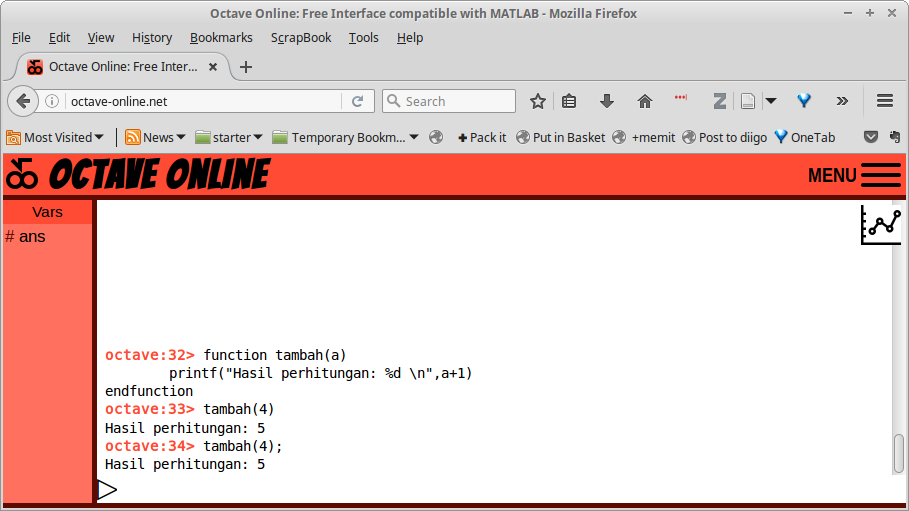 Gambar 24.
Gambar 24.
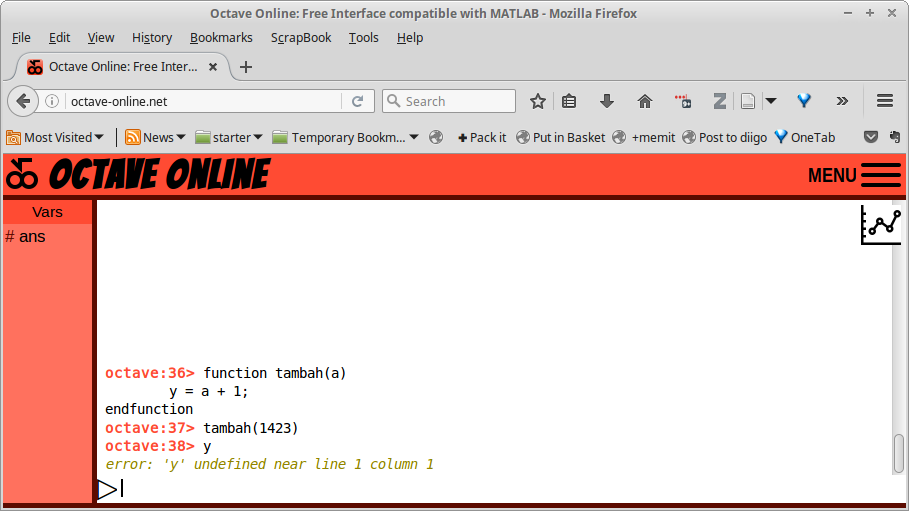 Gambar 25.
Gambar 25.
function y = cariRMS(A) syms x y = A * double(sqrt((1/(2*pi)) * int((sin(x))^2,0,2*pi))) endfunction
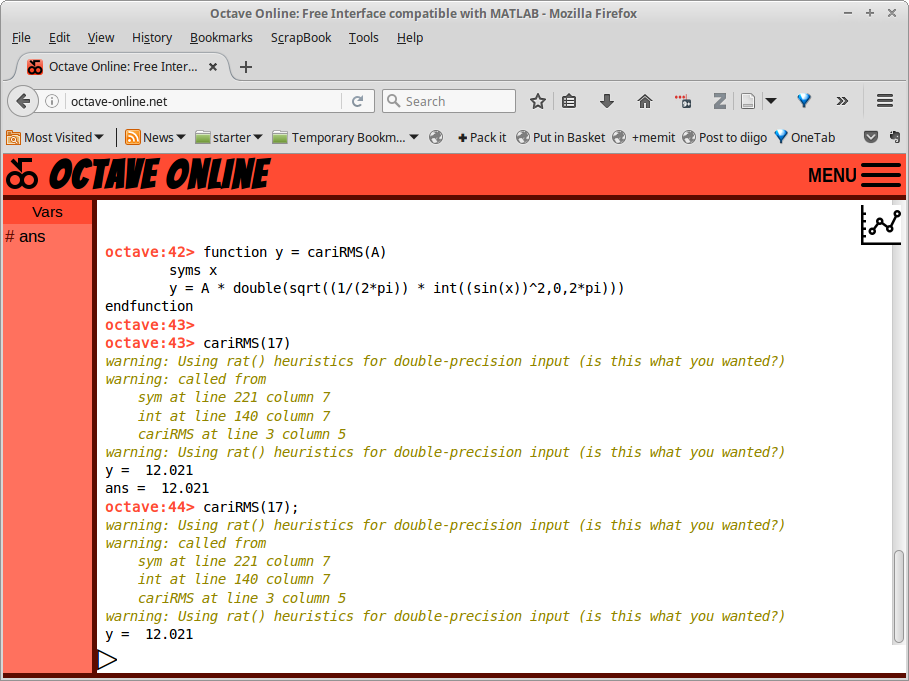 Gambar 26.
Gambar 26.
function y = cariRMS(A)
syms x
y = A * double(sqrt((1/(2*pi)) * int((sin(x))^2,0,2*pi)));
printf("Nilai RMS dari gelombang sinus dengan amplitudo %d adalah: %d \n", A, y);
endfunction
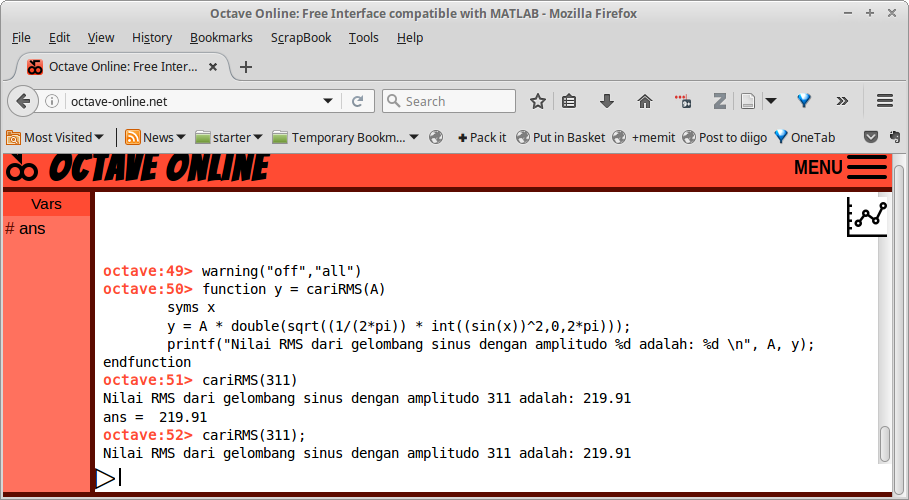 Gambar 27.
Gambar 27.
function y = cariRMS(A)
syms x
y1 = A * double(sqrt((1/(2*pi)) * int((sin(x))^2,0,2*pi)));
y2 = A * (1/(sqrt(2)));
y3 = A * 0.707
printf("Nilai RMS (y1) dari gelombang sinus dengan amplitudo %d adalah: %d \n", A, y1);
printf("Nilai RMS (y2) dari gelombang sinus dengan amplitudo %d adalah: %d \n", A, y2);
printf("Nilai RMS (y3) dari gelombang sinus dengan amplitudo %d adalah: %d \n", A, y3);
endfunction
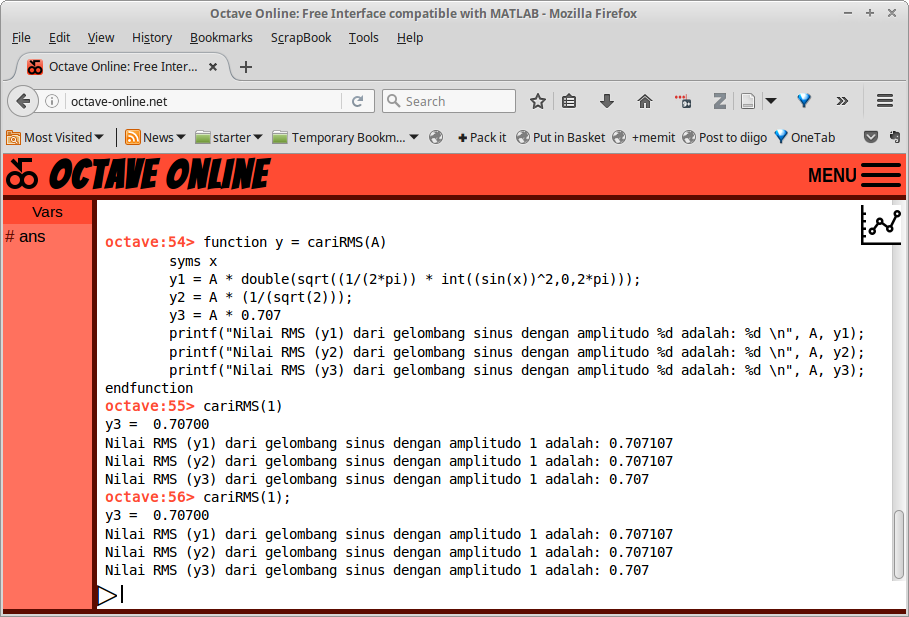 Gambar 28.
Gambar 28.
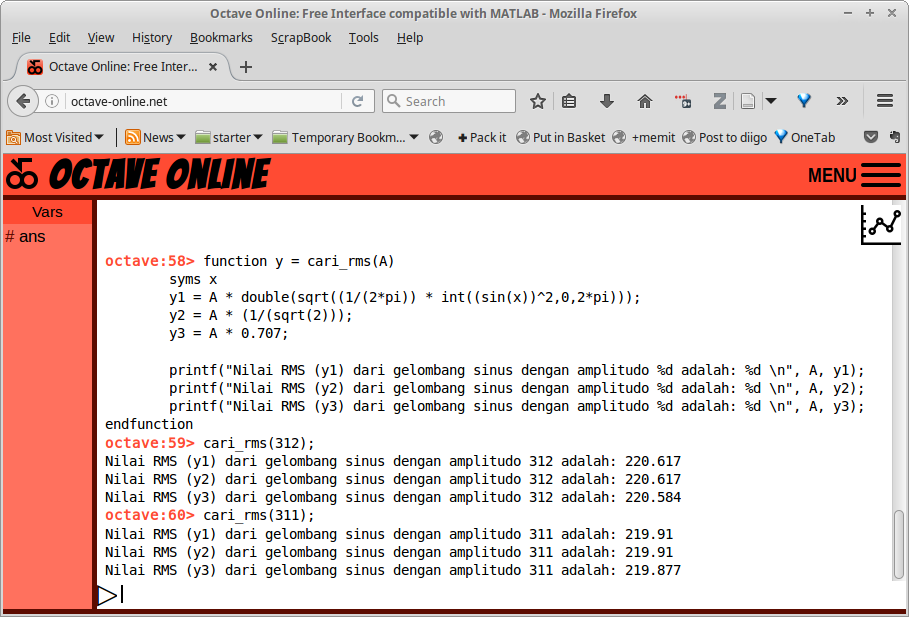 Gambar 29.
Gambar 29.
function y = cari_peak(a_rms)
syms x
y1 = a_rms * 1/double(sqrt((1/(2*pi)) * int((sin(x))^2,0,2*pi)));
y2 = a_rms * (sqrt(2));
y3 = a_rms * 1/0.707;
printf("Nilai peak (y1) dari gelombang sinus dengan nilai rms %d adalah: %d \n", a_rms, y1);
printf("Nilai peak (y2) dari gelombang sinus dengan nilai rms %d adalah: %d \n", a_rms, y2);
printf("Nilai peak (y3) dari gelombang sinus dengan nilai rms %d adalah: %d \n", a_rms, y3);
endfunction
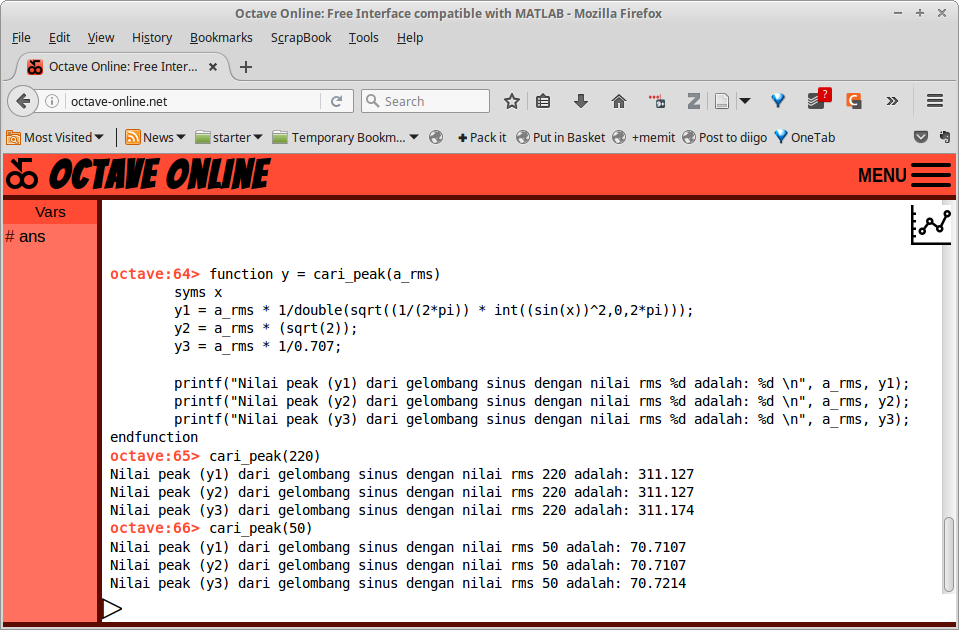 Gambar 30.
Gambar 30.
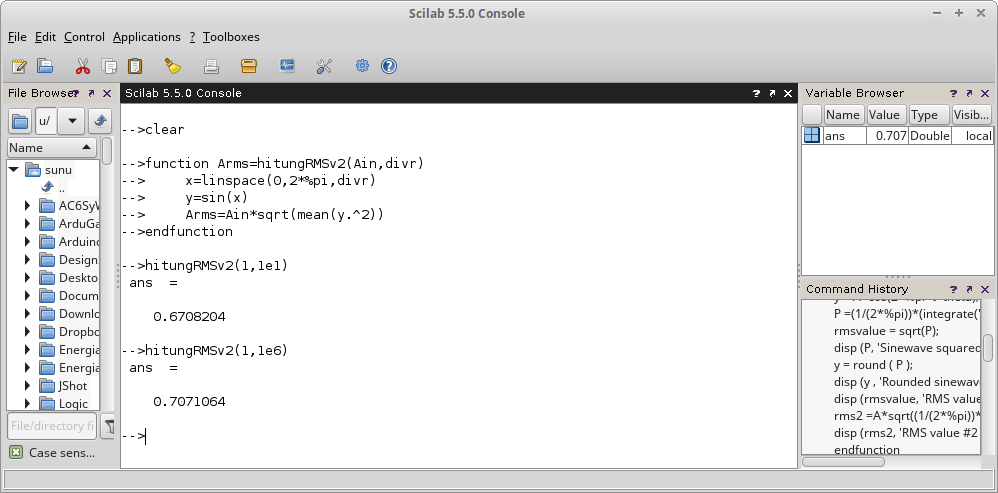 Gambar 31.
Gambar 31.
function Arms=frms(Ain,divr)
x=linspace(0,2*pi,divr);
y=sin(x);
Arms=Ain*sqrt(mean(y.^2));
endfunction
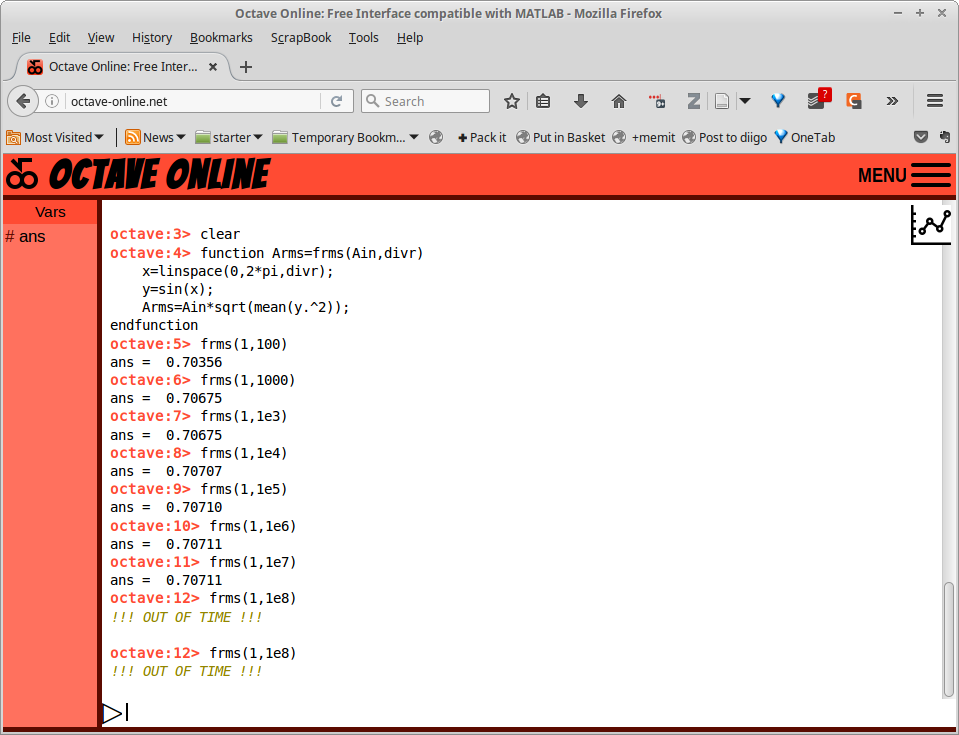 Gambar 32.
Gambar 32.
 Gambar 33.
Gambar 33.
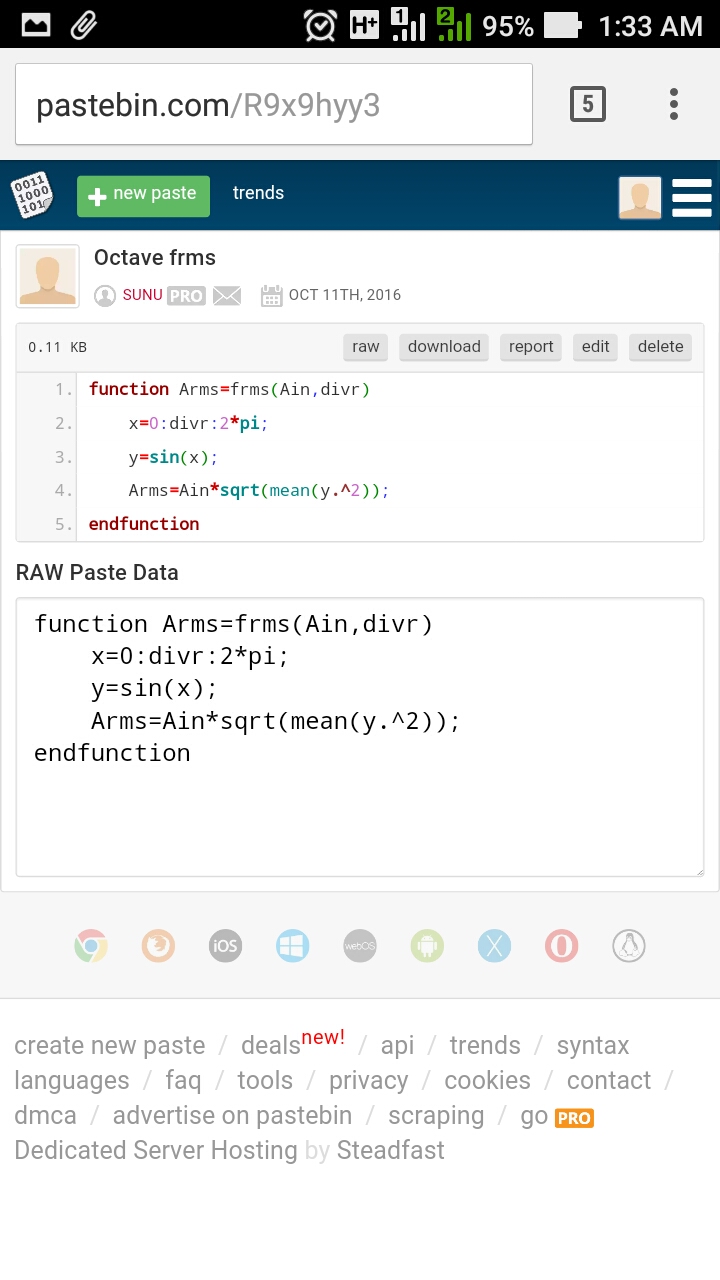
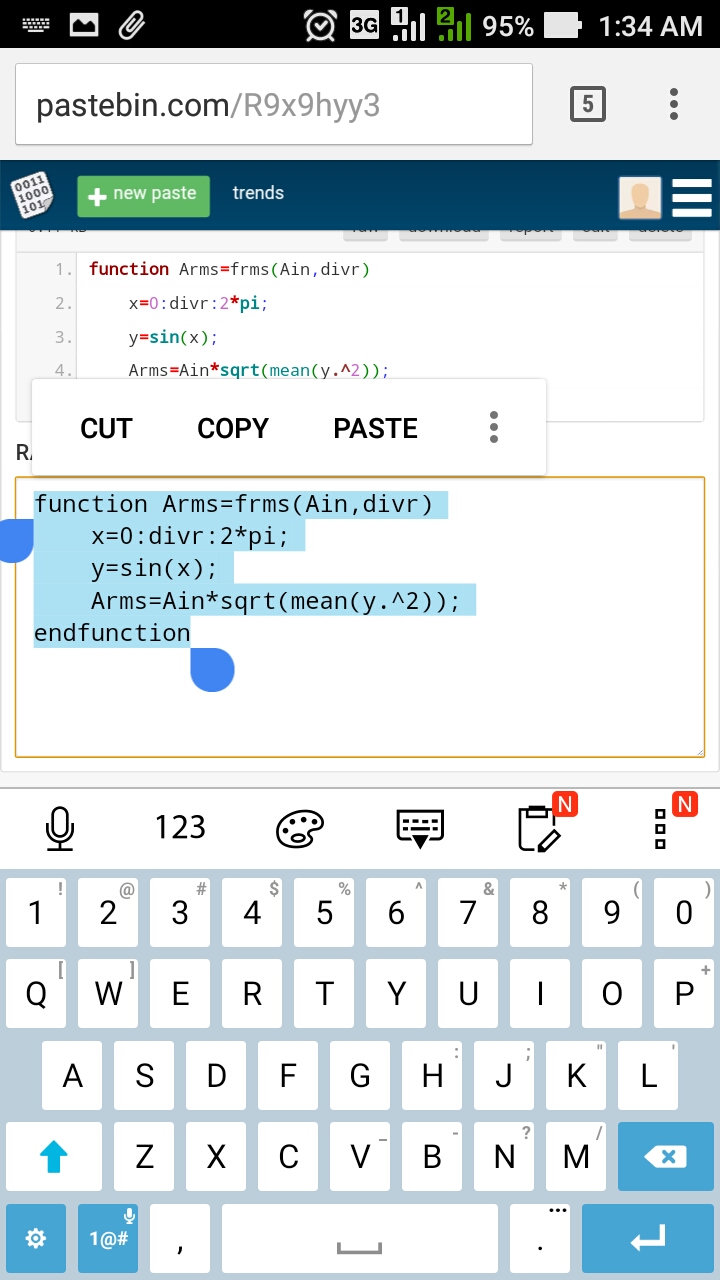
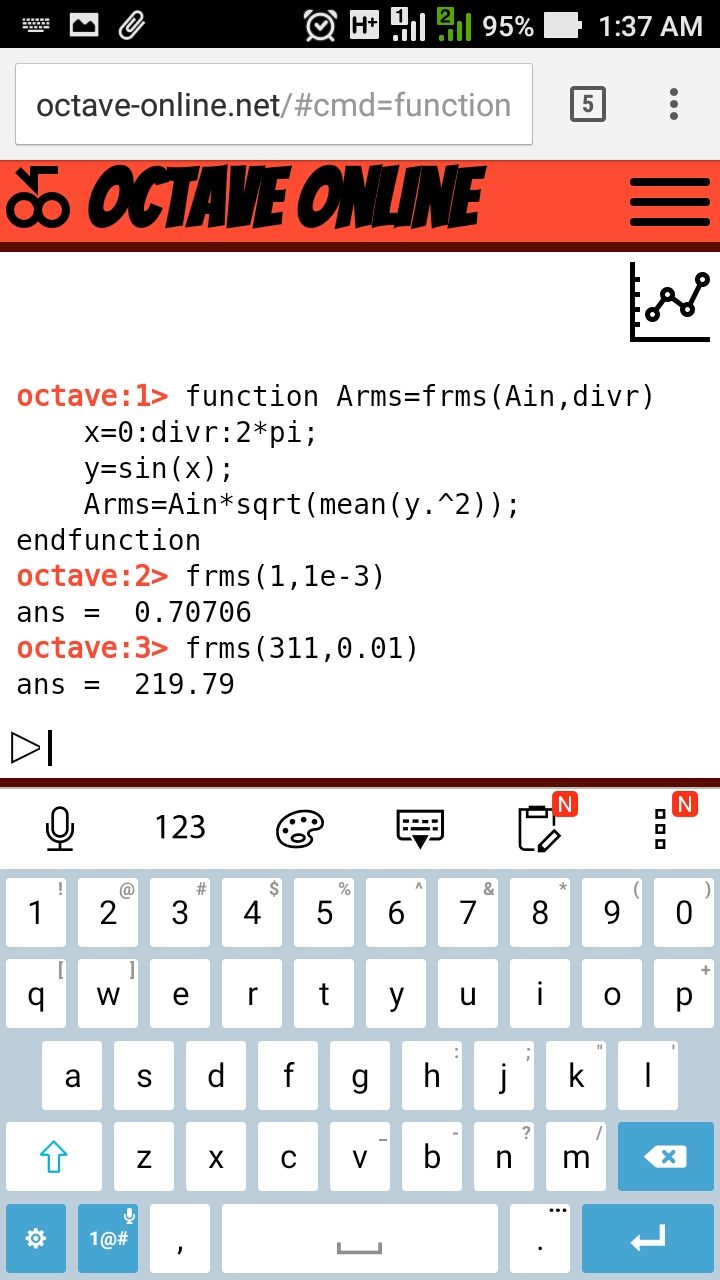
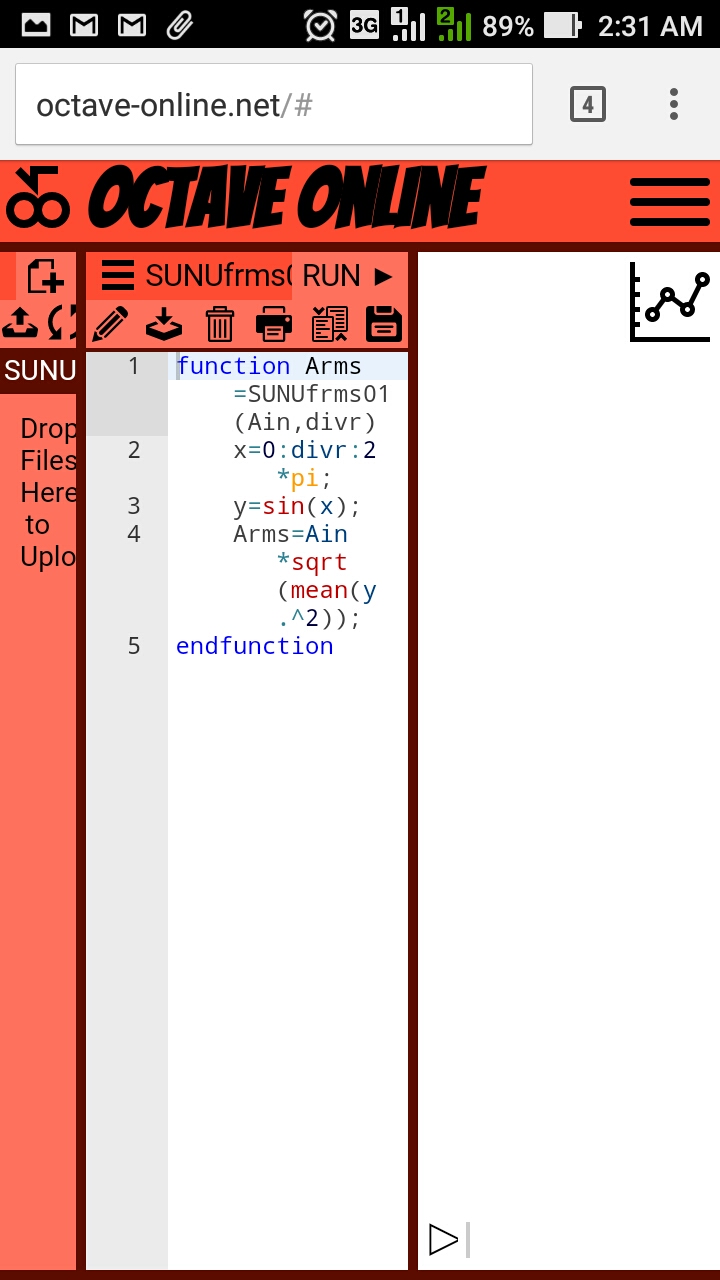
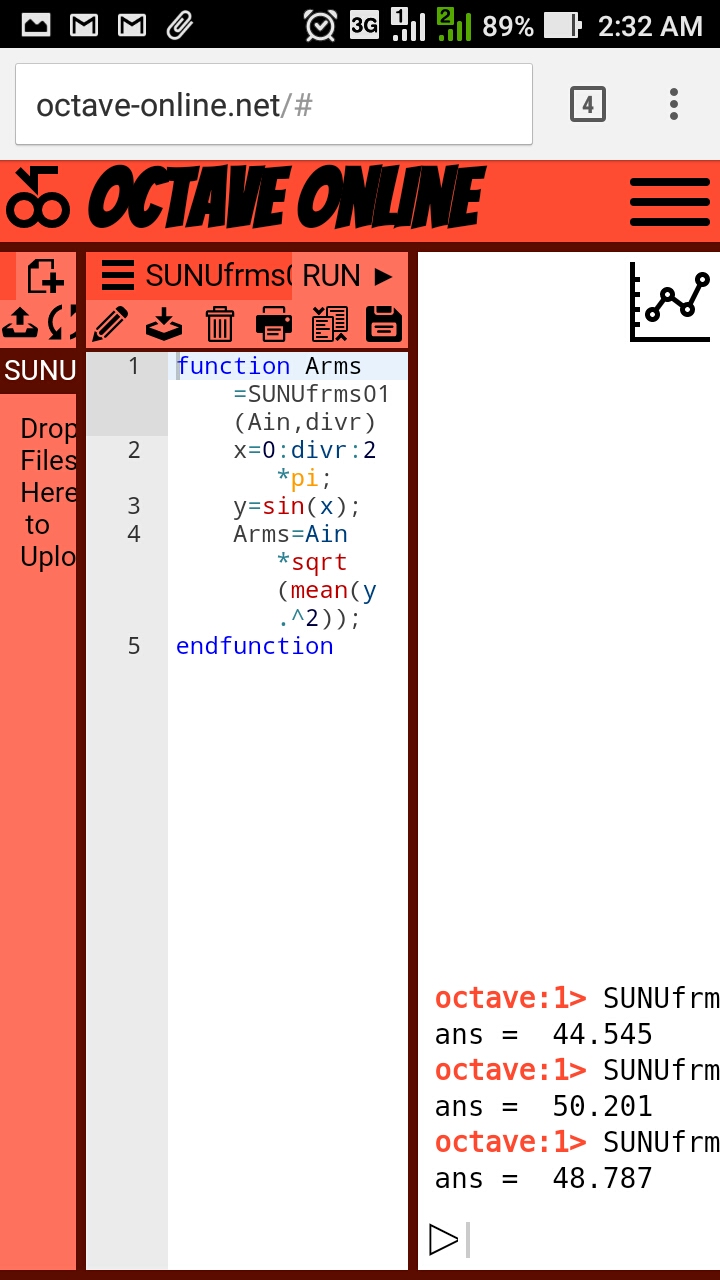
function Arms=frms(Ain,divr)
x=0:divr:2*pi;
y=sin(x);
Arms=Ain*sqrt(mean(y.^2));
endfunction
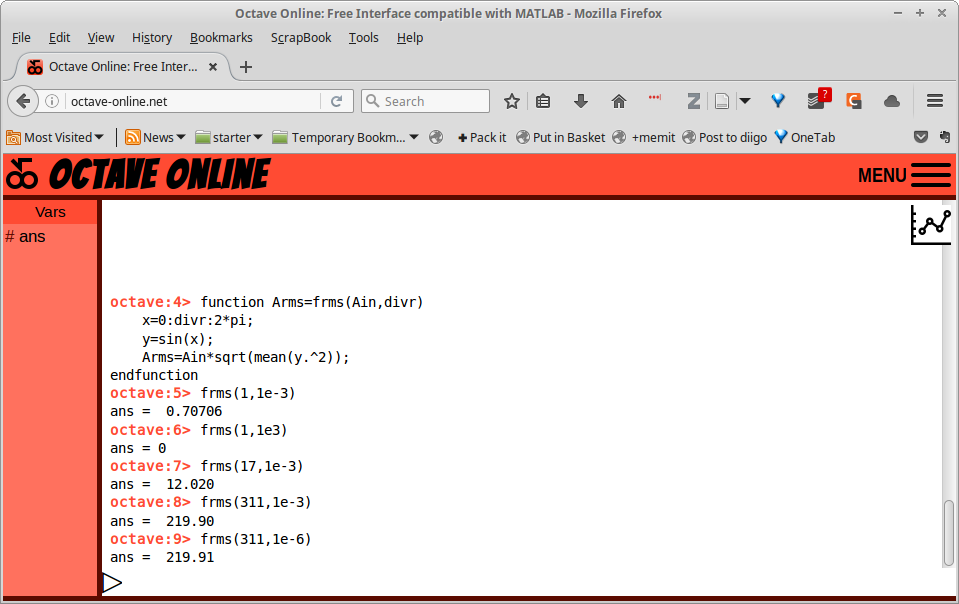 Gambar 34.
Gambar 34.
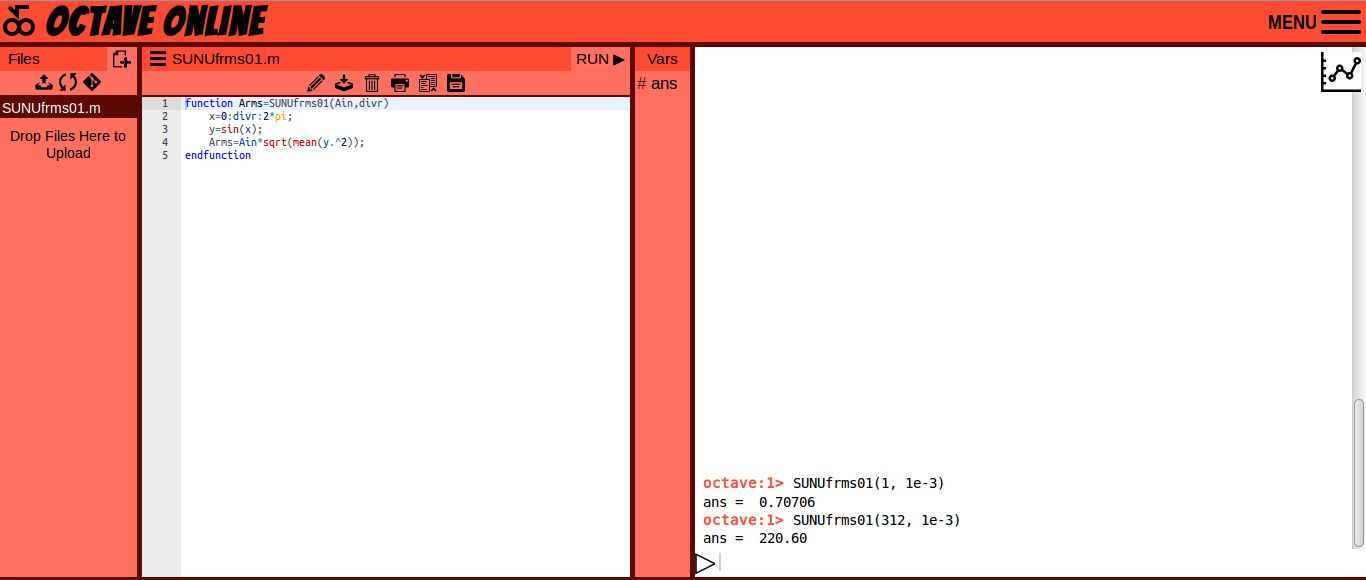 Gambar 42.
Gambar 42.
 Gambar 43.
Gambar 43.
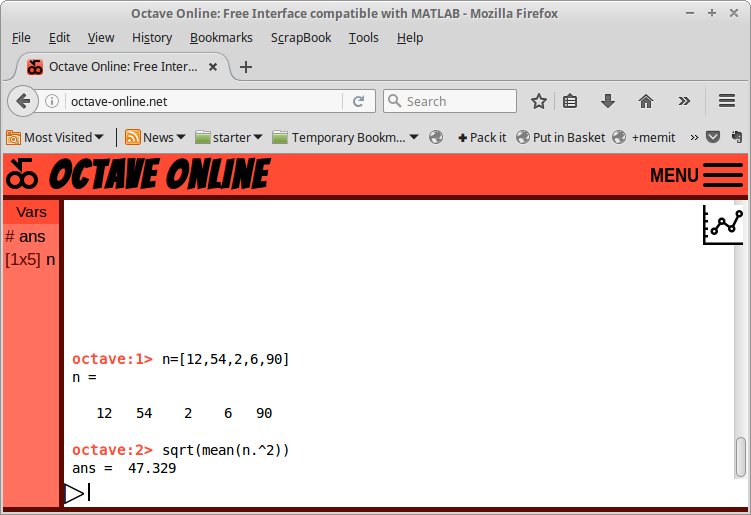 Gambar 45.
Gambar 45.
 Gambar 46.
Gambar 46.
[su_panel border=”2px solid #6699FF” radius=”10″]
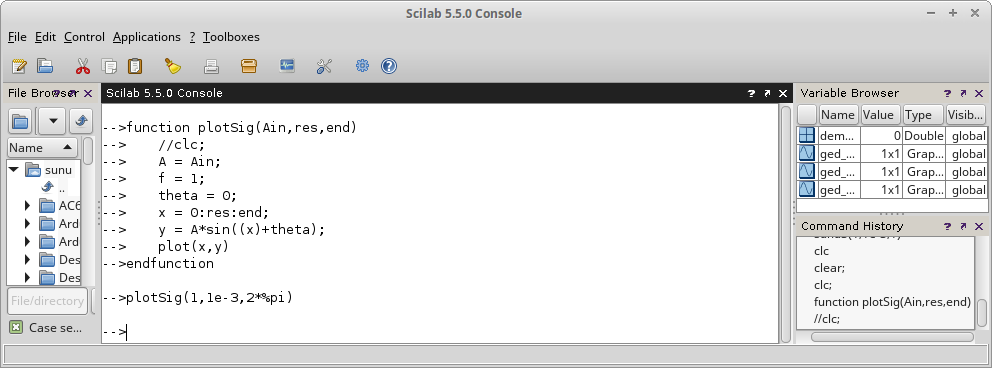 Gambar 47.
Gambar 47.
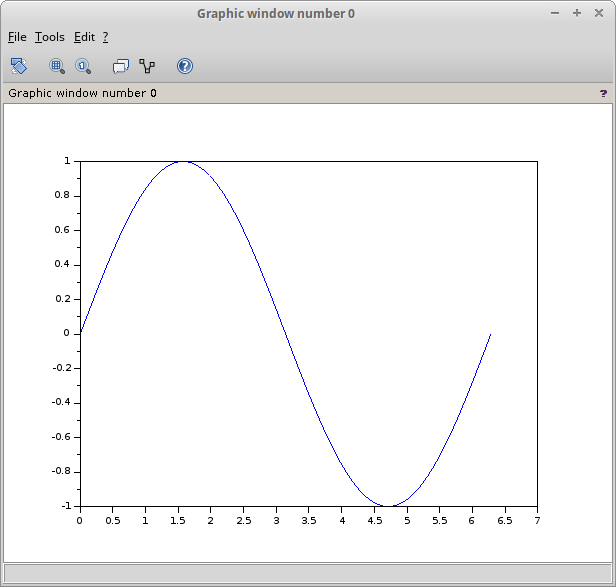 Gambar 48.
Gambar 48.
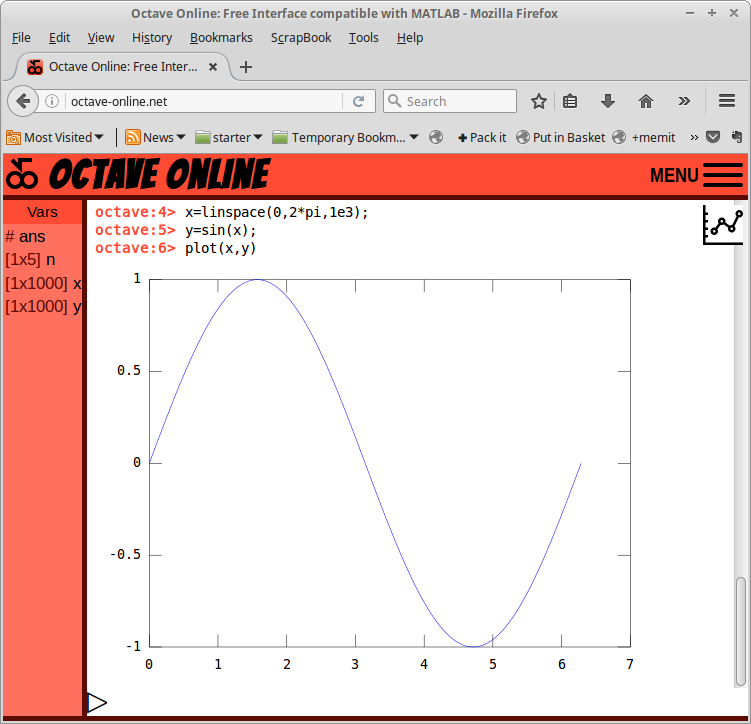 Gambar 49.
Gambar 49.
function n=plotSig(Ain,res,endz)
A = Ain;
f = 1;
theta = 0;
x = 0:res:endz;
y = A*sin((2*pi*f*x)+theta);
plot(x,y)
endfunction
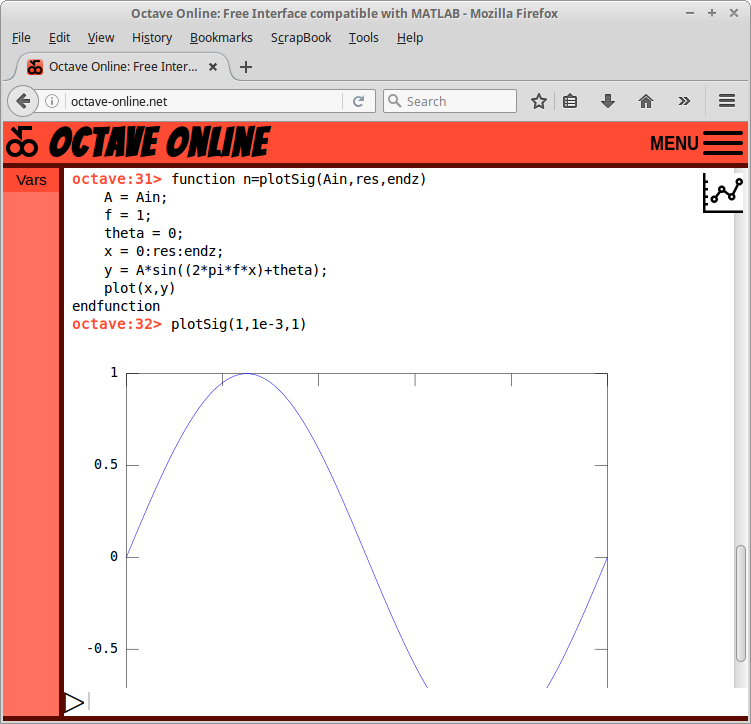 Gambar 50.
Gambar 50.
function n=plotSig(Ain,fin,res,endz)
A = Ain;
f = fin;
theta = 0;
x = 0:res:endz;
y = A*sin((2*pi*f*x)+theta);
plot(x,y)
endfunction
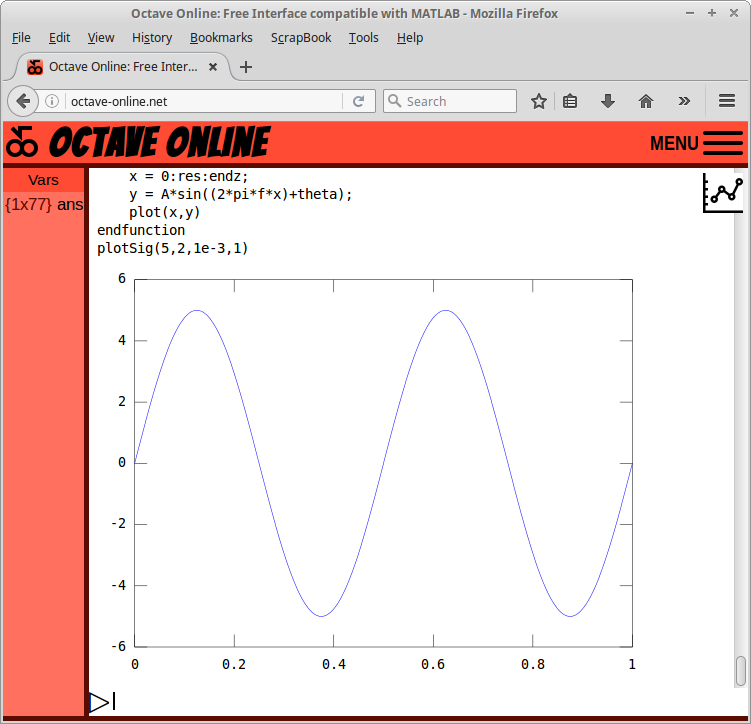 Gambar 51.
Gambar 51.
[/su_panel]